
Беседа вторая. Классическое определение вероятности
Одно из важнейших понятий современной науки - вероятность. Оно используется теперь и в математике, и в науках о природе, и непосредственно в практике - инженерном деле, организации производства, сельском хозяйстве. Современное определение вероятности случайного события требует достаточно широких математических знаний, и поэтому мы вынуждены ограничиться здесь лишь первичным представлением, сложившимся еще в работах пионеров теории вероятности - Б. Паскаля, П. Ферма, X. Гюйгенса (1629-1695) и Я. Бернулли (1654-1705). По этой причине оно и получило наименование классического определения вероятности. Это понятие тесно связано с представлениями о симметрии. С таким положением дел часто приходится встречаться и в наши дни, а потому к классическому определению вероятности нередко обращаются и теперь при решении задач физики, техники, биологии.
Вернемся вновь к примеру о солдате и его вопросах об исходах бросания костей. Какие предположения делаются относительно игральных костей и их бросания? Таких предположений два, а именно, что кости правильны и их бросают без обмана. Слова "кости правильны" и "бросают их без обмана" требуют дополнительных пояснений. Что значит кости правильны? Прежде всего что они являются геометрически точными кубами и что они сделаны из однородного материала, имеющего во всех своих частях одну и ту же плотность. Точно так же бросание кости должно производиться таким образом, чтобы ни одна из граней не имела предпочтения перед другими, в частности, чтобы бросающий не мог заранее предвидеть, какая грань кости должна выпасть.
Но мы могли бы изготовить специальные кости в виде тетраэдра, додекаэдра, октаэдра или икосаэдра. И вновь, не производя предварительных испытаний, могли бы ожидать, что в случае изготовления таких специальных "костей" одной и той же плотности в каждой их части, при соблюдении геометрической правильности и при бросании их "наудачу" все грани должны выпадать одинаково часто. Этот вывод мы делаем на основании реальной симметрии таких костей. Так, при многократном бросании тетраэдра мы будем ожидать, что каждая из граней появится примерно в одной четверти всех бросаний. Если же сделать "правильную" кость в виде икосаэдра, затем произвести, скажем, тысячу бросаний, то каждая из граней появится примерно по пятидесяти раз*.
* (3аметим, что в настоящее время в Японии для иллюстрации использования методов теории вероятностей при производстве сложных вычислений изготовляют кости как раз в виде икосаэдров.)
С ситуациями, когда в результате некоторого испытания может произойти какой-то один из определенного числа n исходов, причем ни один из этих исходов не имеет преимущества перед другими, встречаются часто. Приведем пример, когда приходится иметь дело с таким положением. В тираже хорошо организованной лотереи или же государственного займа перед очередным извлечением может появиться любой номер не имеющий каких-либо преимуществ перед другими. Такие исходы принято называть равновозможными или равновероятными. Само понятие равновероятности является первичным и не поддается строгому математическому определению. Его можно только прояснить и иллюстрировать различными примерами.
Предположим теперь, что при каждом из испытаний может появиться любой из n равновероятных и различных исходов, и притом только один. Обозначим их символами Е1, Е2, ..., Еn. При подбрасывании монеты могут появиться только два исхода - Е1 - герб и E2 - решка. При подбрасывании икосаэдра могут появиться 20 равновероятных исходов, которые мы обозначаем Е1, Е2, ..., Е20. Если в лотерее продан миллион билетов, то при приобретении одного билета имеется миллион равновероятных исходов.
Пусть A - некоторое случайное событие, которое наступает тогда и только тогда, когда наступает какой-то исход из определенных: Еi1, Еi2, ..., Еim. Для примера, при бросании трех игральных костей, как мы видели, возможны 216 исходов. Случайное событие А состоит в выпадении таких граней, для которых сумма проставленных на них чисел равна 12. Мы знаем, что наступление интересующего нас события происходит только в 25 определенных сочетаниях выпавших граней. Все такие сочетания мы выписывали в первой беседе. Про каждый исход, при котором интересующее нас событие наступает, мы станем говорить, что он благоприятствует этому событию.
Если из всех n равновероятных исходов m благоприятствуют событию А, то вероятностью события А называется отношение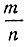 Вероятность события А принято обозначать символом Р{A}.
Вероятность события А принято обозначать символом Р{A}.
В частности, если m = 1, т. е. если событие А совпадает с одним из возможных исходов Еi, то 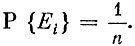
Если событие А таково, что каждый исход благоприятствует его появлению, то такое событие называют достоверным. Чтобы отличить достоверное событие от всех остальных, мы станем обозначать его (и только его) символом U. Достоверному событию благоприятствуют все исходы (т. е. m = n), поэтому
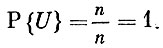
Пример 1. В лотерее выпущено 500 билетов, и среди них 40 выигрышных. Приобретен один билет. Чему равна вероятность того, что на него выпадает выигрыш?
В нашем примере исходов n = 500, и среди них благоприятствующих 40. Таким образом, вероятность того, что приобретенный билет окажется выигрышным равна
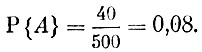
Пример 2. Известно, что в изготовленной партии сопротивлений, состоящей из 1200 изделий, имеется 900 сопротивлений первого сорта, 180 - высшего качества и 120 - второго сорта. Наудачу берется из этой партии одно изделие. Спрашивается, чему равны вероятности того, что оно окажется высшего качества, 1-го сорта, 2-го сорта?
Пусть А, А1 и А2 обозначают последовательно события, состоящие в том, что выбранное событие окажется высшего сорта, 1-го сорта и 2-го сорта. Согласно определению находим, что
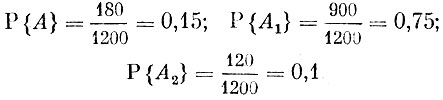
Пример 3. В школе 800 учащихся. Среди них имеются 72, которые по всем предметам систематически получают высшие оценки, и 320 учащихся, систематически получающих высшие оценки не по всем, но хотя бы по одному предмету. Спрашивается, чему равны вероятности того, что первый встреченный нами школьник окажется "отличником" (событие А); получающим систематически высшие оценки не по всем, но хотя бы по одному предмету (событие В)?
Согласно определению
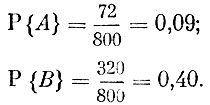
Для дальнейшего нам потребуются некоторые дополнительные сведения, относящиеся к случайным событиям и к действиям с вероятностями.
Суммой событий А и В называется событие, состоящее как из исходов, составляющих А, так и из исходов, составляющих В. Те исходы, которые благоприятствуют как А, так и В, считаются только один раз. Сумма событий А и В обозначается либо А + В, либо символом А∪В.
В только что рассмотренном примере 3 события А и В обозначали соответственно встречу с учеником, который либо систематически получает высшие оценки по всем предметам, либо получает высшие оценки не по всем предметам, но хотя бы по одному.
Очевидно, что событие С = А + В означает встречу с учащимся школы, который получает высшую оценку хотя бы по одному предмету.
Еще один пример. Пусть события А и В означают соответственно следующие события - при бросании игральной кости выпадет четное число очков; при бросании игральной кости выпадет число очков, кратное трем. Какие исходы благоприятствуют событию А + В?
Если через Еk мы обозначим исход, означающий выпадение грани, на которой обозначено k очков, то событию А благоприятствуют исходы Е2, E4, E6, а событию В благоприятствуют исходы Е3 и Е6.
Согласно определению событию А + В благоприятствуют исходы Е2, Е3, E4, Е6.
Заметим, что событие В может быть записано в виде суммы Е3 + Е6.
Понятие суммы, естественно, распространяется на любое число событий А, В,..., N. А именно событие А + В + ... + N состоит из тех и только тех исходов, которые входят в состав хотя бы одного из событий А, В, ..., N.
В последнем примере событие А согласно сказанному может быть записано в виде суммы Е2 + Е4 + Е6.
Если события А и В не имеют совпадающих исходов (иными словами, одни и те же исходы не благоприятствуют сразу и А, и В), то они называются несовместными.
События А и В в только что рассмотренном примере с бросанием игральной кости совместны, поскольку исход Е6 благоприятствует как А, так и В. В примере с учащимися школы события А и В несовместны. Заметим, что если каждые два события среди событий А, В, ..., несовместны, то они несовместны и все вместе (в совокупности).
Важность введенного понятия становится ясной из следующей теоремы, являющейся одним из основополагающих предложений теории вероятностей.
Теорема сложения вероятностей.Если события А и В несовместны, то
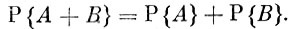
Действительно, пусть событию А благоприятствуют исходы Ei1, Еi2, ..., Eik, а событию В - исходы Еj1, Ej2, ..., Ejm.
Согласно предположению, среди этих двух групп исходов нет ни одного исхода, принадлежащего сразу первой и второй группе. Отсюда следует, что событию С = А + В благоприятствуют все исходы первой и второй группы, т. е. всего k + m исходов. Таким образом, вероятность события С равна
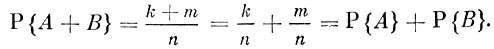
Теорема доказана.
В примере 3 вероятность встречи с учащимся, который систематически получает высшие оценки хотя бы по одному предмету, равна
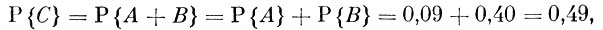
поскольку события А к В несовместны.
События А и В называются противоположными, если они несовместны и в сумме образуют достоверное событие.
Обычно событие, противоположное А, обозначается символом 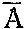 .
.
Событию 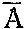 благоприятствуют все те исходы из n равновозможных и несовместимых исходов, которые не благоприятствуют А. Пусть
благоприятствуют все те исходы из n равновозможных и несовместимых исходов, которые не благоприятствуют А. Пусть
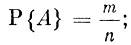
тогда
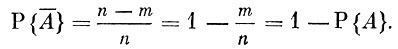
Полученное равенство очень полезно при вычислении вероятностей событий, поскольку нередко вероятность противоположного события вычисляется несравненно проще, чем вероятность прямого.
Пример 4. Бросаются три игральные кости. Чему равна вероятность того, что хотя бы на одной из них появится "шестерка"?
Мы знаем, что общее число равновероятных исходов в нашей задаче равно 63 = 216. В данном примере проще сначала подсчитать вероятность не интересующего нас события А, а противоположного ему события 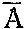 . Противоположное событие состоит в том, что ни на одной из трех брошенных костей не появится "шестерка". Пять исходов благоприятствуют тому, что на кости не появится "шестерка". Чтобы ни на одной из трех костей не появилась "шестерка", необходимо, чтобы на каждой из них появилась грань из пяти отмеченных отличными от шести цифрами. Такое совпадение возможно 53 = 125 различными способами. Таким образом,
. Противоположное событие состоит в том, что ни на одной из трех брошенных костей не появится "шестерка". Пять исходов благоприятствуют тому, что на кости не появится "шестерка". Чтобы ни на одной из трех костей не появилась "шестерка", необходимо, чтобы на каждой из них появилась грань из пяти отмеченных отличными от шести цифрами. Такое совпадение возможно 53 = 125 различными способами. Таким образом,
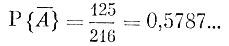
Согласно найденной формуле
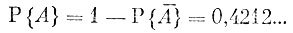
Пример 5. На электрической схеме, изображенной на рисунке 1, расположены выключатели, каждый из которых может быть включен и выключен, причем обе эти возможности одинаково вероятны. Чему равна вероятность, что схема не будет проводить ток?
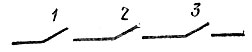
Рис. 1
Всего различных положений трех выключателей может быть 23 = 8. Из них благоприятствующих пропусканию тока будет только одно, а именно то, когда все три выключателя будут включены. Вероятность того, что схема будет проводить ток, таким образом, равна
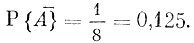
Согласно выведенной нами формуле, искомая вероятность равна
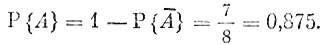
Произведением событий А и В называют событие, состоящее из тех и только тех исходов, которые входят как в А, так и в В.
Пусть бросаются две игральные кости - первая и вторая. Событие А состоит в том, что на первой кости выпадет четное число очков, а событие В - в том, что на второй кости выпадет число очков, кратное трем. Всего равновероятных исходов в нашем примере 36, все их можно записать как пары чисел (k, l), где k и l могут принимать любые целые значения между 1 и 6. Событию А благоприятствуют 18 исходов - все пары (k, l), в которых на первом месте стоит четное число (2, 4 или 6). Событию В благоприятствуют 12 исходов - все пары (k, l), в которых на втором месте стоит число, кратное трем (т. е. 3 или 6). Событию АВ благоприятствуют лишь шесть исходов - (2, 6), (4,6), (6,6), (2,3), (4,3), (6,3).
Произведение событий А и В обозначается одним из символов АВ или А∩В.
Обратим внимание на то, что в том множестве случайных событий, которое было введено в рассмотрение, операции умножения событий и разыскания противоположного события выполнимы не всегда. В самом деле, если А и В не содержат общих исходов, то событие, противоположное достоверному, не содержит ни одного благоприятствующего ему исхода. Чтобы исключить такую возможность выхода за пределы случайных событий при операциях над случайными событиями, расширяют само понятие случайного события. А именно, мы введем в рассмотрение невозможное событие, которому не благоприятствует ни один исход. Обозначим невозможное событие символом V. Теперь мы гарантированы, что операции над случайными событиями не выведут нас за пределы множества случайных событий. В частности, теперь мы можем написать равенство V = 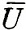 , а также противоположное ему равенство U =
, а также противоположное ему равенство U = 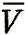 . Отсюда (так же как и из определения невозможного события) следует, что Р {V} = 0.
. Отсюда (так же как и из определения невозможного события) следует, что Р {V} = 0.
Мы можем теперь обобщить теорему сложения вероятностей и распространить ее на тот случай, когда о событиях А ж В уже не предполагается, что они несовместны. Мы докажем сейчас, что каковы бы ни были события А и В
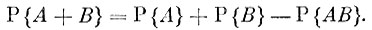
Действительно, пусть событиям А и В благоприятствуют соответственно кит исходов. События А и В могут быть совместными. Это означает, что и тому и другому благоприятствуют в том числе и одни и те же l исходов. Таким образом, эти l исходов, и только они, благоприятствуют событию А В, Теперь ясно, что событию А + В благоприятствуют k + m - l исходов. Отсюда и следует формула.
В качестве иллюстрации доказанной формулы рассмотрим такой пример: события А и В соответственно означают, что при бросании игральной кости выпадают грани с четными очками, выпадают грани с очками, кратными трем. В данном примере k = 3, m = 2, l = 1, n = 6. Таким образом, вероятность того, что при бросании кости выпадет грань с четным числом очков или числом очков, кратным трем, равна
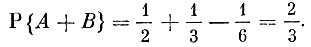
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'