Беседа девятая. Источники нового в математике

Предшествующее изложение убедительно показывает, что практика является одним из важнейших источников новых проблем и понятий в математике. Зачастую она предлагает математикам такие вопросы, которые выходят за пределы ранее имевшихся идей и тем самым вызывают на поиски новых методов и подходов описания и исследования. Об этом источнике нового настолько хорошо и убедительно сказал в одной из своих публичных лекций П. Л. Чебышев, что я считаю необходимым привести оттуда довольно большую цитату.

"Несмотря на ту высокую степень развития, до которой доведены науки математические трудами великих геометров трех последних столетий, практика обнаруживает ясно неполноту их во многих отношениях: она предлагает вопросы существенно новые для пауки и, таким образом вызывает на изыскание совершенно новых методов. Если теория много выигрывает от новых приложений старой методы или от новых развитии ее, то она еще более приобретает открытием новых метод, и в этом случае наука находит себе верного руководителя в практике"^*.

^* (Чебышев П. Л. Черчение географических карт.- Полн, собр. соч. М., Изд-во АН СССР, 1951, т. 5, с. 150.)

В развитии математики, велика роль практики, но к ней одной нельзя свести источники нового в нашей науке. В математике развиваются не только области исследований, которые находят немедленные применения. Многие из математических работ посвящены проблемам, практические возможности которых не видны даже в обозримом будущем. Однако математики не безразличны к нуждам общества. Некоторые из проблем, стоящих перед техникой, сельским хозяйством, медициной, экономикой и другими областями деятельности, превращаются в источник постоянных размышлений и приводят к постановке новых математических задач. Не это ли имел в виду Давид Гильберт, когда говорил в своем знаменитом докладе на II Международном математическом конгрессе в Париже, что "каждый век имеет свои проблемы".

Мы должны также иметь в виду, что само представление о связях математики с практикой претерпело серьезные изменения. Зачастую эти связи уже перестали быть непосредственными, и математические идеи, методы, понятия нередко оказываются отделенными от практики несколькими ступенями абстрагирования. Требования практики чаще всего воздействуют на технику, та в свою очередь обращается за помощью к физике, и лишь последняя ставит задачу перед математикой. Но как бы ни был сложен путь от практики к математике, влияние ее на прогресс математических знаний сохраняется.

Я хотел бы сейчас рассказать совсем кратко о двух областях исследований, первые шаги которых были связаны самым непосредственным образом с задачами практики. Одна из них - теория приближения функций - возникла в начале второй половины XIX века в работах великого русского математика, члена ряда зарубежных академий наук, в том числе парижской, П. Л. Чебышева. В 1856 г. ему пришлось прочесть курс практической механики для студентов, в котором, в частности, следовало изложить теорию употребительных в ту пору механизмов. Его внимание привлек так называемый параллелограмм Уатта, использовавшийся в технике для превращения вращательного движения в поступательное (а также поступательного во вращательное), в частности, в паровых машинах. В действительности параллелограмм Уатта не давал точного поступательного движения. Это обстоятельство приводило к быстрому износу движущихся частей и потере мощности паровых машин.

Чебышев решил создать механизм, который давал бы минимально возможную ошибку (отклонение) от прямолинейного на заданном интервале движения. В результате была сформулирована следующая задача: среди всех полиномов

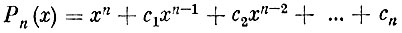
найти тот, который имеет наименьшее уклонение от нуля на всем промежутке (-1, +1).

Выяснилось, что для каждого n существует единственный полином такого рода. Все корни такого полинома действительны и расположены в отрезке (-1, +1). Эти полиномы обозначаются в честь Чебышева^* символом Т_n(х), и для них имеет место равенство

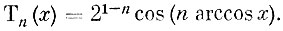
^* (На французском языке фамилия Чебышева пишется так; Tche´bychcv.)

В частности, при начальных значениях n полиномы Чебышева даются формулами:

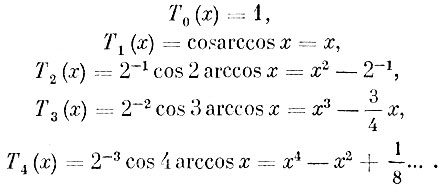
Наибольшее уклонение полинома T_n(x) от 0 в отрезке (-1, +1) равно ¹/_2^n-1; оно достигается в указанном отрезке n+1 раз (попеременно положительные и отрицательные). Полиномы Чебышева получили многочисленные применения как в теоретической, так и в прикладной математике.

Вслед за задачей о разыскании полиномов, наименее уклоняющихся от нуля, с видом которых мы только что познакомились, Чебышев выдвинул более общую задачу и решил ее - задачу о разыскании такой линейной комбинации заданных непрерывных функций φ_k (x), которая бы приближалась к непрерывной функции f (х) в отрезке (а, b) лучше всего. Иными словами, речь идет о том, чтобы так подобрать коэффициенты с₀, с₁, ..., с_n, чтобы максимальное значение абсолютной величины разности

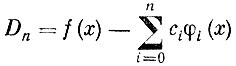
во всем отрезке (а, b) было наименьшим.

Результаты самого П. Л. Чебышева и его многочисленных последователей составили содержание большой и важной теории, получившей название теории наилучшей аппроксимации функций. Важно отметить, что эта теория находит многочисленные применения в различных областях знания, в том числе и прикладных.

Другой пример относится уже в значительной мере к нашему времени. После того как в работах Максвелла, Больцмана, Гиббса и других ученых кинетическая теория газов, жидкостей и твердых тел принесла многочисленные плоды> ряд исследователей пришли к твердому убеждению, что математические средства изучения явлений природы с позиций молекулярного строения вещества еще недостаточны. Уже Анри Пуанкаре в самом начале нашего века высказывал мысль, что статистическая физика нуждается в развитии новой главы теории вероятностей, в которой рассматривались бы не только случайные величины, но и процессы, т. е. случайные величины, изменяющиеся во времени. Независимо от Пуанкаре и совсем по другому поводу, связанному с изучением закономерностей смены гласных и согласных звуков в русском языке, близкую задачу начал изучать А. А. Марков (1856-1922). Им были заложены основы теории последовательностей особым образом связанных между собой случайных величин, получивших, по предложению французского математика Жака Адамара (1865-1963), название цепей Маркова. Эти идеи позднее, уже в тридцатые годы были использованы Н. Винером, А. Н. Колмогоровым, А. Я. Хинчиным для построения теории случайных процессов, т. е. теории случайных величии, зависящих от одного параметра, который обычно называют временем. При этом все названные авторы имели в виду при построении теории определенные физические явления: Н. Винер - броуновское движение, А. Н. Колмогоров - процессы диффузии, А. Я. Хинчин - общие идеи статистической физики. В результате А. Н. Колмогоров построил общую теорию процессов без последействия или иначе - основы теории марковских процессов; Н. Винер ввел в рассмотрение частный случай процессов без последействия, который теперь известен под названием процессов Винера; А. Я, Хинчин развил теорию стационарных случайных процессов.

В наше время теория случайных процессов превратилась в основную главу теории вероятностей и получила многочисленные применения в физике, радиоэлектронике химии, геофизике, биологии и других областях знания.

Как ни важен для теории постоянный обмен идеями с практикой, только им невозможно объяснить ее прогресс. Имеется и другой источник ее развития, без которого она превратилась бы в сборник рецептов и потеряла значительную часть своей познавательной ценности. Я имею в виду внутренние проблемы математики, ее стремление к общности понятий и результатов и их завершенности, независимо от возможных применений. Это не только даст ей значительную самостоятельность развития, но и позволяет опережать требования практики.

В том бурном потоке исследований, который наблюдается в наши дин, когда только по математике ежегодно публикуются тысячи работ и доказываются десятки тысяч новых теорем, предлагаются новые теории и методы исследования, как никогда ранее, требуется обобщающая мысль. Иначе все это собрание идей и фактов превратится в неуправляемый хаос. Разрозненные идеи, методы и факты, отдельные частные выводы способны нас подавить своей массой. Без предварительного приведения их в систему трудно, а порой и невозможно ими пользоваться. Они только тогда превратятся в орудие познания и смогут служить и в каком-то определенном частном случае и во множестве других, когда отдельные результаты и понятия будут максимально n разумно обобщены. Вот почему перед математиками постоянно возникает вопрос: найденная закономерность является изолированным фактом или же звеном целой цепи? Открытие такой взаимосвязи результатов позволяет на обнаруженные ранее факты взглянуть с более общих позиций и подметить элементы порядка там, где была лишь аморфная масса полезных идей, понятий и теорем. Вот почему перед математикой всегда со всей настойчивостью возникает необходимость построения общей математической теории. Я позволю себе проиллюстрировать эту мысль на примере.

В самом начале XVIII века Яков Бернулли доказал для последовательности взаимно независимых испытаний важную теорему, которая впоследствии получила наименование закона больших чисел в форме Бернулли^*. Речь шла о доказательстве следующего интуитивно ясного результата. Пусть в каждом из n независимых испытаний некоторое событие А может произойти с вероятностью, равной р. Если через и. обозначить число появлений события А в n испытаниях, то разность 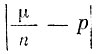при точно больших n будет, как правило, мала.

^* (См. беседу четвертую второй части книги.)

При этом, поскольку для и, возможны значения - 0, 1, 2, ..., n, возможные значения 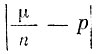могут изменяться от р до 1-р.

Спустя тридцать с небольшим лет А. Муавр (1667-1754) получил более глубокий результат, получивший впоследствии название предельной теоремы Муавра-Лапласа. Приблизительно еще сто лет потребовалось, чтобы С: Пуассон (1781-1840) распространил эти факты на схему независимых испытаний, но с вероятностями р появления события А, зависящими от номера испытания. Заметим, что эти теоремы он получил в связи с изучением задач теории стрельбы.

В середине прошлого века О. Коши исходя из задач теории ошибок наблюдений, обнаружил, что при суммировании одинаково распределенных независимых случайных величин при увеличении числа слагаемых их распределения сближаются с особым типом распределений, которые получили впоследствии наименование устойчивых. В теории вероятностей происходил процесс накопления разрозненных фактов.

В 1867 г. появилась в печати знаменитая теорема П. Л. Чебышева, в которой исключительно просто был доказан закон больших чисел^* в весьма общей форме. Теоремы Бернулли и Пуассона содержались в нем в качестве простейших частных случаев. Естествознание получило новый сильный метод исследования, позволяющий из структуры явления предвидеть окончательный результат.

^* (См. беседу шестую второй части книги.)

Через тридцать лет появилась новая работа П. Л. Чебышева, в которой было дано глубокое обобщение теорем Муавра-Лапласа и Пуассона, касавшихся сближения функций распределения сумм независимых случайных величин с так называемым нормальным распределением. Эти результаты П. Л. Чебышева вызвали интерес ряда других исследователей - А. А. Маркова, А. М. Ляпунова (1857-1918), а позднее П. Леви (р. 1886), С. Н. Бернштейна (1880-1968), В. Феллера (1906-1970), А. Я. Хинчина (1894-1959), А. Н. Колмогорова (род. 1903) и многих других, которые существенно продвинули изучение этой области математической мысли.

Одновременно с чисто теоретическим развитием первоначальных вопросов развивалось и использование построенной теории в статистической физике, биологии, инженерном деле. Ранее разрозненные факты становились элементами большой и содержательной теории. Создание теории приводило к совершенствованию методов доказательства, упрощению рассуждений, более глубокому и ясному пониманию существа тех условий, в которых удавалось обнаружить правильность тех или иных закономерностей. Далее, оттачивались форма и система изложения, дававшие возможность с единых позиций излагать большие группы вопросов, ранее казавшихся далекими друг от друга.

Третий источник новых проблем в математике связан с ее обоснованием, т. е. с критическим пересмотром ее исходных положений, основных понятий, представлений о полноте и строгости доказательств, выявлением центральных направлений математической мысли. И это абсолютно необходимо как для сохранения единства математики, так и для приведения логического фундамента в соответствие с ее содержанием. Такой пересмотр был осуществлен в прошлом веке и связан с именами О. Коши, К. Вейерштрасса и ряда других выдающихся ученых. В начале XX века вновь был произведен подобный пересмотр на базе теории множеств, созданной в своих основах Г. Кантором (1845-1918). Каждый из этих этапов развития математики дал толчок ее бурному прогрессу, выявив множество ранее не замечавшихся возможностей развития и глубоких связей между далекими областями исследований.

Математика меняла свое лицо, но при этом становилась более гибкой и цельной, получала несравненно более широкие возможности для изучения окружающего нас мира. Одновременно были созданы предпосылки для развития новых продуктивных ветвей математики - функционального анализа, теории случайных процессов и т. д. Наконец был открыт путь новым математическим концепциям - неконструктивным доказательствам, широкому развитию чистых теорем существования.

Проблемы обоснования математики не снимаются с повестки дня и теперь, поскольку математика бурно растет ив ней возникают новые понятия, новые области исследования. Широкую программу работ в этом плане в течение последних десятилетий проводила группа французских математиков, известная под именем Никола Бурбаки. Их концепции вызвали большой интерес во всем математическом мире.