Беседа шестая. Математические модели

Прежде чем какое-нибудь явление природы или же экономический, технический (или какой бы то ни было иной) процесс подвергнуть математическому изучению, оно должно быть подвергнуто упрощению. Из всего многообразия свойств, присущих явлению, следует отобрать лишь те, влияние которых будет учитываться.

Модель явления не тождественна самому явлению, она дает некоторое приближение к явлению и к его пониманию. Эта модель может быть весьма схематической и тем не менее давать вполне удовлетворительное приближение к действительности. Вспомним, что небесная механика со времени Ньютона исходит из такой модели устройства Солнечной системы: планеты и Солнце представляют собой материальные точки с соответствующими массами, и между ними действуют силы тяготения согласно закону

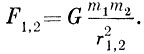
Здесь F_{1, 2} - сила тяготения между небесными телами 1 и 2 с массами, соответственно равными m₁ и m₂, расстоянием между их центрами тяжести, равным r_{1, 2}, G - постоянная тяготения. Материальные точки, моделирующие планеты, расположены в центрах тяжести соответствующих планет. Как ни схематична эта модель на первый взгляд, она вполне удовлетворительно отражает движения планет и дает возможность вычислять взаимное положение планет на небосводе на многие годы с поразительной точностью. Более того, за последнее столетие она дважды позволила путем вычислений предсказать наличие в Солнечной системе планет, которые до того не наблюдались астрономами. Исходя из неправильностей движения самых далеких от Солнца известных в те времена планет был сделан вывод, что они. вызваны наличием еще одной планеты. Сравнив фактические уклонения с теми, которые получались в предположении существования еще одной планеты, удалось вычислить неизвестные массу, расстояние до Солнца и положение на небесном своде для определенного момента времени. Так в 1846 г. была открыта планета, получившая название Нептун, в результате вычислений, выполненных независимо друг от друга и одновременно У. Лаверье (1811-1877) и Дж. Адамсом. Подобные же вычисления, выполненные П. Лоуэллом, привели в 1930 г. к открытию девятой планеты Солнечной системы, получившей название Плутон.

Для одного и того же явления можно предложить много моделей, основанных на различных принципах и исходящих из различных схематизации. История науки оставила нам огромное число примеров такого рода. Скажем, в оптике рассматривались несколько моделей природы света: корпускулярная, волновая, электромагнитная. Для всех этих моделей были выведены многочисленные закономерности количественного характера. Каждая из них требовала своего особого математического аппарата. Корпускулярная оптика пользовалась средствами элементарной геометрии и пришла к выводу законов отражения и преломления света. Модель волновой теории света потребовала новых математических идей как для вывода известных результатов, так и для получения новых. Чисто аналитическим путем были открыты законы интерференции и дифракции света и не наблюдавшиеся ранее. Геометрическая оптика, связанная с корпускулярной моделью, оказалась при этом бессильной. Так были получены дополнительные аргументы в пользу волновой теории. Но и эта теория уступила свое место электромагнитной теории света, поскольку появились такие факты, которые она уже не могла объяснить.

Вполне может случиться, что несколько моделей могут одинаково удовлетворительно описывать явление. Обычно это случается лишь до некоторых пределов, начиная с которых одна из них оказывается предпочтительнее, обладает большими возможностями. До этих пор нет основания (если только нет других преимуществ у одной модели перед другими) предпочесть одну модель другим. Они все имеют равные права на существование. Но с того момента, когда явление не получает достаточного совпадения с предсказаниями модели или же не может быть объяснено ею, от нее приходится отказаться и искать замену, отражающую явление полнее, объясняющую как ранее известные, так и новые факты. При этом старые модели могут и не отбрасываться совсем, а сохраняться в науке, но уже для ограниченных целей.

Для примера, геометрическая оптика продолжает широко использоваться в теории и на практике, хотя сейчас приняты другие модели природы света.

Создание математической модели - важный этап познания. Приходится четко формулировать наши представления о ходе интересующего явления и о действующих в нем связях. Мы перечисляем сделанные нами предположения, и если в ходе опытной проверки или при сравнении реального течения процесса с предвычисленными состояниями согласно математической модели наблюдаются расхождения, то появляется возможность исследования влияния каждого из сделанных исходных предположений. Без такого четкого перечисления исходных положений нет возможности опытным путем проверить степень соответствия развиваемой теории природы явления, для объективного сравнения различных теорий.

Остановимся кратко на одном иллюстративном примере, связанном с решением несложной инженерной задачи. В связи со значительной ролью технических систем в жизни общества все большее значение придается увеличению их надежности. Это достигается многими путями, одним из которых является резервирование, когда в систему вводятся дополнительные элементы, без которых она может обойтись. Цель их - продление работоспособности системы, когда соответствующий элемент потеряет возможность работать. Запасное колесо автомобиля как раз является таким резервным элементом, и его ставят на место колеса, в котором спустила покрышка. Если отказавший элемент направляется на ремонт, а затем возвращается в резерв, то такие системы называются резервированными системами с восстановлением. Если основной элемент и все резервные окажутся в нерабочем состоянии, то говорят, что резервированная система с восстановлением отказывает. Тогда задача состоит в следующем: на сколько резервирование с восстановлением увеличивает длительность безотказной работы системы?

Понятно, что так поставленную задачу еще нельзя решать, поскольку нам еще ничего не известно, еще нет базы, на которой можно строить логические рассуждения и выводить формулы для инженерных расчетов. Само собой разумеется, что основой модели должны быть наблюдения и инженерная интуиция. В результате длительных обсуждений со специалистами была принята такая модель:

1. Длительность безотказной работы элемента системы есть случайная величина с некоторым распределением вероятностей F (x).
2. Длительности безотказной работы последовательно включаемых элементов - независимые случайные величины с одним и тем же распределением.
3. Отказ элемента обнаруживается немедленно.
4. Отказавший элемент немедленно направляется в ремонт.
5. Длительность ремонта - случайная величина с распределением вероятностей G (x).
6. Если имеется хотя бы один исправный элемент, замена отказавшего элемента на исправный произведшей мгновенно.
7. Отремонтированный элемент немедленно поступает в резерв.
8. Длительность ремонта не зависит от того, как долго продолжался период его безотказной работы.
9. Ремонт полностью восстанавливает свойства элемента. Только что описанная модель резервирования с восстановлением уже может служить исходным пунктом для получения необходимых выводов. Ряд перечисленных предпосылок может вызвать известную неудовлетворенность и желание заменить их на более реальные. И о об этом несколько позднее. Сейчас же приведем простое следствие из приведенной модели при одном дополнительном условии.
10. Резервные элементы находятся в ненагруженном состоянии, т. е. в период их пребывания в резерве они не изменяют своих свойств.

Если наша система состоит из одного рабочего и одного резервного элемента в ненагруженном резерве, то средняя длительность Т безотказной работы системы связана со средней длительностью безотказной работы одного элемента а следующей формулой

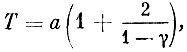
где 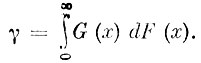Смысл величины прост - это вероятность того, что длительность восстановления окажется меньше длительности безотказной работы элемента. Чем ближе у к единице, тем больше Т. Для чего необходимо: или увеличить длительность безотказной работы элемента или же уменьшить длительность ремонта.

В приведенной нами модели особую неудовлетворенность могут вызвать пункты 4, 7, 9. Действительно, мы знаем, что каждая смена неисправного элемента требует некоторого времени; после ремонта элемент никогда не восстанавливает свои свойства полностью. Хорошо известно, что средняя длительность безотказной работы автомобиля после первого капитального ремонта составляет приблизительно 70-80% от средней длительности безотказной работы нового автомобиля. Можно изменить эти положения модели и тем самым несколько усложнить модель, приблизив ее одновременно к реальным условиям. Однако во многих случаях предложенная модель вполне удовлетворительно описывает реальную обстановку и позволяет получить полезные для практики формулы, оценить целесообразность восстановления и резервирования для каждой интересующей нас технической системы.

В настоящее время математическое моделирование используется и в тех случаях, когда о физической структуре явления известно крайне мало. В этом случае строится гипотетическая модель и на ее основе выводятся следствия, уже доступные наблюдению. Но такие модели зачастую не оправдываются опытом. В этом случае их жизнь коротка, они быстро умирают и уступают место другим моделям, позволяющим глубже проникнуть в природу вещей. К такого рода моделям и гипотезам приходится прибегать для подготовки к исследованию космических тел. Так, при посылке космической станции на Венеру пришлось производить расчеты при целой гамме гипотез о величине давления и составе окружающей ее атмосферы.

Все же ценность гипотетических моделей неоспорима: они способствуют работе мысли, наводят экспериментаторов на идеи новых экспериментов, позволяют продвигаться в познании окружающего нас мира. История пауки показывает, сколь большую роль играли научные гипотезы и построенные на их основе математические модели явлений в астрономии и физике. Вспомним гипотезу строения Солнечной системы Коперника и сделанные на ее основе многочисленные выводы, существенно продвинувшие человечество по пути знания и разбудившие пытливость разума. Вспомним далее модель строения атома, предложенную Резерфордом, по которой атом построен примерно так же, как Солнечная система: вокруг ядра атома вращаются электроны. Сама модель оказалась недостаточной, и дальнейшее развитие науки ее откинуло, но она вызвала к жизни исследования, которые привели к современной физике атома и к первым шагам на пути покорения таящейся в недрах атома энергии.

В настоящее время возникла настоятельная необходимость обратить особое внимание на построение математических моделей биологических и социальных явлений. Они исключительно сложны и требуют для своего изучения всех возможных методов, созданных наукой. Такие проблемы, как построение теории работы памяти, предупреждение психических заболеваний, нуждаются не только в наблюдениях, но и в построении математических моделей, в том числе и гипотетических. Логическим путем из них можно будет получить следствия. Часть этих следствий окажется доступной для наблюдения, для количественного сравнения совпадения теории с опытом. Но при этом необходимо длительное сотрудничество биологов, психологов, психиатров и математиков с физиками и химиками. В последние годы в этом направлении проводятся интересные работы, в частности, в новой научной области, получившей название бионики. Бионика стремится выдвигать новые технические идеи на базе того, что уже осуществила природа в живых существах. Непосредственное опытное исследование процессов мышления исключительно трудно, поскольку любое экспериментирование над процессом мышления имеет весьма ограниченные возможности и неизбежно оказывает серьезное психологическое воздействие на объект наблюдений. Именно поэтому так важно иметь для продвижения в познании этих процессов хорошие математические модели.

Неисчерпаемые возможности для построения математических моделей имеются также в педагогике. Однако эта проблема очень сложна и начинать работу следует с самых простых, быть может, даже почти игрушечных задач. Математике давно пора стать в педагогике не только предметом преподавания, но и методом исследования. К педагогике не меньше чем к другим областям знания относятся знаменитые слова К. Маркса^*: "...наука только тогда достигает совершенства, когда ей удается пользоваться математикой". Человечество крайне заинтересовано в том, чтобы педагогика была наукой совершенной.

^* (Воспоминания о Марксе и Энгельсе. М., Госполитиздат, 1956.)