Беседа пятая. Очереди в жизни и их математические модели

Современная жизнь связана с потерями на ожидание в различного рода очередях. Мы ожидаем при переходе улицы у светофора, на приеме у зубного врача, самолет, встречая друзей, автобус на остановке и т. д. С возникновением очередей приходится считаться и в подавляющем большинстве вопросов научной и практической деятельности. Действительно, при прохождении речных судов через шлюзы неизбежно образуются очереди как в верхнем, так и в нижнем бьефе. В морском порту, принимающем грузовые суда дальнего плавания, приходится считаться с тем, что в момент прибытия очередного судна в порту заняты все причалы и оно должно будет ожидать своей очереди для погрузки или разгрузки, пока не освободится один из доступных ему причалов от обслуживания ранее прибывших судов. В крупных аэропортах постоянно происходит почти одновременный прилет или отправление самолетов. В результате приходится организовывать очередь на взлет и посадку, чтобы избежать аварий. На ткацких фабриках ткачихе поручается обслуживание нескольких десятков станков. В обязанности ткачихи входит наблюдение за правильностью работы каждого из них и в случае возникновения неполадок (обрыв нитей утка или основы, необходимость смены челнока и т. д.) их исправление. Однако может случиться (и действительно случается), что, пока ткачиха занята у одного станка, неполадки случаются на другом или других. В результате образуется очередь на обслуживание из порученных ей станков. Такого же рода ситуации создаются и в современных вычислительных, управляющих и информационных машинах. Скажем, пока информационная машина принимает (или выдает) одну информацию, возникнет необходимость принимать также другие.

Естественно, что в таких условиях возникают многочисленные вопросы: какова длительность ожидания начала обслуживания? Какая может образоваться очередь на обслуживание? Сколько обслуживающих единиц целесообразно иметь в системе? При данном числе обслуживающих единиц как велика будет их загрузка?

Остановимся несколько подробнее на особенностях работы станции скорой медицинской помощи какого-нибудь района города. На эту станцию поступают вызовы от больных, которым требуется срочная помощь врача. Для обслуживания больных имеются врачебные бригады и автомобили. В том случае, когда вызов поступил в момент наличия хотя бы одной свободной бригады, она немедленно отправляется по указанному адресу. Если же все врачи заняты на предыдущих вызовах, то больной должен ожидать. При этом нет возможности заранее указать, как долго продлится это ожидание, поскольку неизвестно, сколько времени придется пробыть у постелей больных, ранее обратившихся за помощью, и как много времени придется потратить на переезды. К тому же моменты вызовов случайны, а не спланированы заранее. Таким образом, работа станции скорой медицинской помощи должна быть организована в условиях многократной случайности: нам неизвестны ни число вызовов от больных, ни моменты их поступления, ни длительности обслуживания (т. е. длительности того времени, которое врач будет вынужден провести у постели больного). И вот в условиях этой неопределенности нужно заранее определить необходимое число врачей, вспомогательного персонала, машин скорой помощи. И определить это следует так, чтобы больные врачебную помощь получали своевременно, а длительные ожидания были бы лишь досадным недоразумением. Ведь в каждом случае задержки помощи имеется возможность тяжелых, а то и непоправимых последствий.

Известно, что в современном естествознании и в ряде важных областей прикладного знания широко используется прибор для оценки интенсивности ядерного излучения, носящий название счетчика Гейгер - Мюллера. Одна из особенностей действия этого прибора состоит в том, что частица, попавшая в счетчик и сосчитанная им, вызывает в нем разряд, который запирает на некоторое время прибор и не позволяет подсчитывать вновь попавшие в него частицы. Вообще говоря, это "мертвое время" зависит от характера зарегистрированной частицы (в частности, от величины ее заряда), но часто в ядерной физике ограничиваются предположением, что это время постоянно. Мы видим, таким образом, что показания счетчика Гейгер - Мюллера не дают истинного представления о потоке частиц, поскольку некоторые из них вообще не регистрируются. Возникает естественный вопрос о тех поправках, которые необходимо ввести в показания счетчика, чтобы скорректировать их. Обратим внимание на то, что сам поток частиц нерегулярен и промежутки времени между последовательными поступлениями частиц в счетчик являются независимыми случайными величинами. Мы вновь оказались в ситуации, которая была обрисована в предыдущем примере.

Нетрудно привести множество других примеров, взятых из самых разнообразных областей деятельности. Можно описать ситуации, связанные с простоями судов перед шлюзами, автомашин перед светофорами, покупателей в магазинах у касс и прилавков, станков в ожидании ремонтной бригады и т. п. Хорошо известно, что очереди стали настоящим бичом современной жизни, и люди тратят ощутимую часть своей жизни в очередях на автобус, в столовую, в театральную кассу, на работе у пунктов выдачи инструмента и т. п. Вот в чем причина того внимания, которое в настоящее время обращено во всех странах мира на изучение закономерностей образования очередей. Сейчас мы уже можем говорить о том, что такая теория создана и находит многочисленные применения в теории связи, при решении транспортных задач, в задачах организации работы предприятий, в информационных системах и т. д.

В плане математических исследований первичной задачей этой теории следует называть построение моделей входящего потока требований на обслуживание. Особенно важно указать такие модели, которые в общих чертах хорошо передают особенности реальных потоков. Для примера, во многих случаях приходится сталкиваться с таким положением дел, когда поток требований, поступающий в систему обслуживания, складывается из огромного числа частных потоков, независимых между собой. Именно так образуется поток грузовых судов, прибывающих в данный морской порт: он является суммой потоков судов в данный порт из множества других портов мира. Поток вызовов в пункт скорой помощи складывается из потоков вызовов от отдельных граждан. Поток вызовов от абонентов, поступающий на коммутационную аппаратуру центральной телефонной станции, складывается из потоков вызовов от отдельных абонентов и т. д.

Сейчас имеется теорема, доказанная при весьма общих условиях, которые сводятся к следующим: слагаемых потоков очень много, они все независимы между собой, каждый из них вносит ничтожно малый вклад по сравнению с суммарным вкладом всех остальных - суммарный поток обязан быть близким к потоку Пуассона. Иными словами, суммарный поток в высказанных условиях близок к потоку, который обладает двумя следующими свойствами: а) вероятность того, что за промежуток времени t произойдут n событий потока, равна

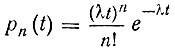
(здесь n может принимать значения 0, 1, 2, 3, ... - любые неотрицательные целочисленные значения, X - положительный параметр); б) в неперекрывающиеся промежутки времени числа наступивших событий - независимые случайные величины.

Мне самому приходилось исследовать статистические данные о прибытии грузовых судов дальнего плавания в морские порты; о поступлении вызовов от тяжелых больных на станции скорой медицинской помощи; о регистрации космических частиц, попадающих на данную площадку земной поверхности. Во всех случаях пуассоновский поток давал превосходную близость с реальными наблюдениями. Описываемая модель образования входящего потока требований не единственна, но удачна.

Уже в первых работах, посвященных телефонному обслуживанию, стали рассматривать два типа систем. В системах первого типа требование, попавшее на обслуживание в момент, когда все приборы уже заняты, становится в очередь и ожидает столько времени, сколько потребуется. Они называются системами с ожиданием. Суда в морском порту образуют как раз систему с ожиданием. В системах другого типа требование, заставшее все приборы занятыми, немедленно покидает систему и уже не возвращается на обслуживание. Этот тип систем получил название систем с потерями. К ним принадлежит система действия счетчиков Гейгер - Мюллера. Обе названные системы отличаются не только техническими деталями, но и характером возникающих при их изучении математических задач. Действительно, для оценки качества обслуживания системой с ожиданием особенно существенно указание средней длительности ожидания начала обслуживания. Для систем же с потерями эта характеристика не имеет ни малейшего интереса. Здесь важно найти другую величину - вероятность того, что вновь поступившее требование будет потеряно системой и тем самым не будет обслужено.

Сейчас уместно сделать одно замечание, которое должно показать, что арифметический подход к решению возникающих в этой проблематике задач приводит к ошибочным результатам и нужны существенно иные подходы, учитывающие специфику исследуемых процессов. Проиллюстрируем это утверждение на простом примере, заимствованном из реальной практики.

До последнего времени вычисление необходимого в порту числа причалов для того, чтобы справиться с планом грузоперевозок, производилось на основании следующих соображений: пусть в течение года в порту нужно переработать (погрузить и разгрузить) Р (2 000 000) тонн и средняя грузоподъемность отдельного судна равна р (5000) тонн. Тогда в течение года должно быть обработано в порту ^Р/_р судов (в примере 2 000 000 : 5000 = 400 судов). Если каждое судно требует для своей обработки t суток (5 суток), то в течение года причалы порта будут р заняты в течение 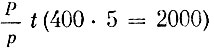суток. Если порт открыт для работы в течение k (250) суток в течение года, то каждый день нам нужно предоставлять под обработку 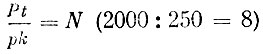причалов. Таким образом заключают, в порту достаточно иметь N (8 в примере) причалов, чтобы выполнить задание плана.

Однако выяснилось, что практика показывала другое: в портах росли простои судов в ожидании обработки, а вместе с тем росли и потери. Причем рост потерь и судового времени и материальных средств на оплату простоев был. непропорционально большим по сравнению с ростом грузооборота. Естественно возникала необходимость произвести анализ правильности используемого решения, выяснения принципиального просчета в таком подходе.

С этой целью проанализируем наше рассуждение и найдем ту неявно используемую предпосылку, на которой оно базируется. Эта предпосылка состоит в том, что в момент освобождения причала в порту должно быть судно, которое немедленно займет его. А это возможно лишь в одном из двух случаев:

а) суда прибывают в порт точно в момент освобождения причалов,

б) в порту имеется очередь судов, ожидающих погрузки и разгрузки.

Первая возможность неосуществима для судов дальнего плавания, поскольку моменты их прибытия не строго фиксированы и длительность погрузо-разгрузочных работ, в зависимости от характера и количества груза, занимает от нескольких часов до многих суток. В результате мы должны заключить, что арифметический подход к решению поставленной задачи ошибочен и его можно называть методом планирования очередей. К сожалению, этот метод расчета весьма распространен и наносит огромный вред народному хозяйству страны. На этом примере мы еще раз убеждаемся в том, как важно прививать учащимся привычку критического отношения к полученному решению, самостоятельно мыслить и ответственность за порученное дело.

В последние годы, в связи с расширением круга практических задач, для решения которых используют теорию массового обслуживания, резко возросло разнообразие ситуаций. Оказалось, что системы с потерями и ожиданием являются лишь частью иных, не менее интересных систем обслуживания: системы с ограниченным временем ожидания, системы с ограниченным временем пребывания (ожидание + обслуживание), системы с ограниченным числом мест ожидания и т. д. Много новых вопросов возникло в связи с эксплуатацией и проектированием информационных и управляющих машин, а также с постановкой нескольких вычислительных или логических задач на одной ЭВМ одновременно. Большое значение приобретают экономические постановки вопросов, когда и содержание системы, и содержание требований в очереди приносит определенные расходы и нужно довести до минимума потери или до максимума прибыль.

Задачи, связанные с проектированием и эксплуатацией систем обслуживания, входят в качестве важной составной части новой прикладной математической дисциплины - исследования операций.