
3. Новые опыты, относящиеся к проблеме Плато
Опыты с пленками не сводятся к демонстрации минимальной поверхности, натянутой на замкнутый контур (как у Плато); диапазон их гораздо шире. В последнее время проблема минимальных поверхностей была изучена не только для одного ограничивающего контура, но и для системы таких контуров; кроме того, было обращено внимание и на возможность образования минимальных поверхностей более сложной топологической структуры. Так, существуют односторонние минимальные поверхности и минимальные поверхности рода, отличного от нуля. Возникающие более общие проблемы порождают изумительное разнообразие геометрических явлений, которые могут быть продемонстрированы с помощью - мыльных пленок. Заметим в этой связи, что очень полезно проволочные каркасы делать гибкими и изучать изменение формы поверхности пленки под влиянием непрерывной деформации каркаса. Дадим описание некоторых опытов.
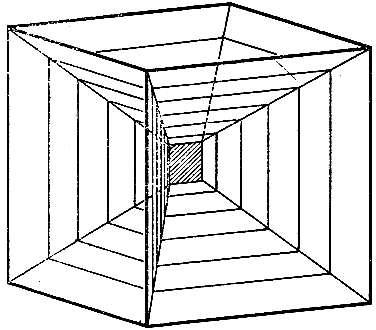
Рис. 240. На кубическом каркасе натянуто 13 почти плоских поверхностей
- Если граничный контур представляет собой окружность, то получается поверхность в виде кругового диска. Можно было бы ожидать, что при непрерывной деформации контура минимальная поверхность всегда будет сохранять тот же топологический характер. Но это неверно. Если изогнуть контур так, как показано на рис. 241, то вместо поверхности, топологически эквивалентной диску, получается односторонняя лента Мёбиуса.
Обратно, можно производить деформацию, исходя из контура, изображенного на чертеже, с натянутой на него пленкой в виде ленты Мёбиуса. Для осуществления непрерывной деформации следует припаять к каркасу рукоятки (см. тот же рисунок). В процессе обратной деформации наступает момент,когда внезапно топологический характер пленки меняется и возникает снова поверхность типа диска (рис. 242). Опять, обращая деформацию, мы вернемся к поверхности Мёбиуса. Замечательно, однако, то, что "мутация" дискообразной поверхности в поверхность типа Мёбиуса происходит на более поздней стадии деформации, чем при обратном процессе. Это показывает, что существует непрерывная цепь замкнутых пространственных контуров, для которых и поверхности типа Мёбиуса, и дискообразные поверхности устойчивы, т. е. доставляют относительные минимумы. Но если поверхность типа Мёбиуса обладает значительно меньшей площадью, чем другая, то эта последняя все же слишком неустойчива, чтобы существовать физически.
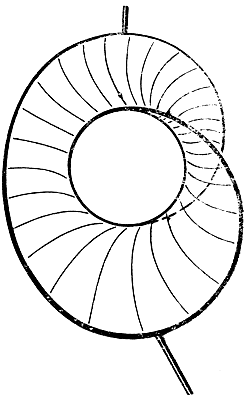
Рис. 241. Односторонняя поверхность (лента Мёбиуса)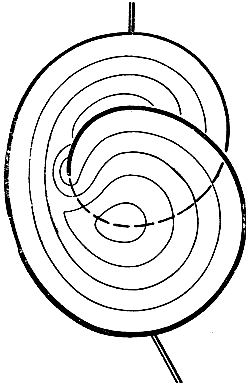
Рис. 242. Двусторонняя поверхность - Можно натянуть минимальную поверхность на систему контуров, состоящих из двух окружностей. Вынув каркас из раствора, мы получаем не одну поверхность, а структуру, состоящую из трех поверхностей, смыкающихся под углом в 120°; одна из них - обыкновенный круговой диск, плоскость которого параллельна плоскостям граничных окружностей (рис. 243). Уничтожая этот диск, мы получим, далее, классический катеноид (поверхность, образуемую вращением цепной линии, о которой шла речь на стр. 415, около прямой, перпендикулярной к оси симметрии). При раздвигании граничных контуров наступает момент, когда двусвязный катеноид лопается и превращается в два отдельных диска. Указанный процесс, конечно, необратим.
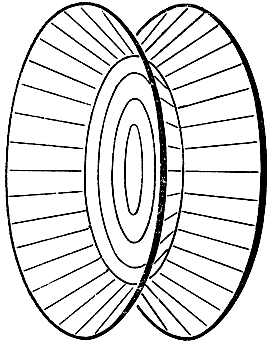
Рис. 243. Система трех поверхностей - Еще один замечательный пример доставляется каркасом, изображенным на рис. 244-246; на этот каркас могут быть натянуты три различные минимальные поверхности. Одна из них (рис. 244) имеет род 1, тогда как две другие односвязны и в некотором смысле обладают свойством взаимной симметрии. Две последние поверхности имеют одну и ту же площадь, если только контур вполне симметричен. Но в противном случае только одна из поверхностей обеспечивает абсолютный минимум площади, тогда как другая - только относительный (мы предполагаем при этом, что минимум разыскивается только по отношению к односвязным поверхностям). Возможность образования поверхности рода 1 обусловливается тем обстоятельством, что, допуская поверхности рода 1, можно получить поверхность меньшей площади, чем для какой бы то ни было односвязной поверхности. При деформации контура мы придем, если только деформация будет достаточно сильно выражена, к такому положению, когда указанное свойство будет уже утеряно: тогда поверхность рода 1 потеряет свою устойчивость и, внезапно разрываясь, превратится в односвязную поверхность одного из двух типов, изображенных на рис. 245 и 246. Если, с другой стороны, мы станем исходить из поверхности одного из этих двух типов, например изображенного на рис. 246, то возможно деформировать контур таким образом, что другой тип (см. рис. 245) станет гораздо более устойчивым. Следствием этого явится тот факт, что в определенный момент произойдет внезапный переход от одного типа к другому. Медленно обращая всю деформацию в обратном направлении, вернем контур снова к исходному положению, но уже с иной натянутой на нем минимальной поверхностью. Можно снова повторить весь процесс в обратном направлении; таким образом, можно многократно повторять переход от одного типа поверхности к другому. Оперируя контуром надлежащим образом, удается также трансформировать одну из односвязных поверхностей в поверхность рода 1. Для этой цели нужно сблизить между собой те части контура, на которые натянуты дискообразные части самой поверхности - с таким расчетом, чтобы поверхность рода 1 стала гораздо более устойчивой. Иногда в процессе выполнения описанной выше операции с контуром возникают промежуточные пленочные поверхности: их нужно уничтожать, чтобы получилась поверхность рода 1.
Этот пример показывает не только возможность решения проблемы Плато различными поверхностями одного и того же топологического типа, но и поверхностями иного типа, причем на одном и том же контуре; кроме того, он снова иллюстрирует прерывный переход от одного решения к другому, в то время как граничные условия проблемы меняются непрерывно.
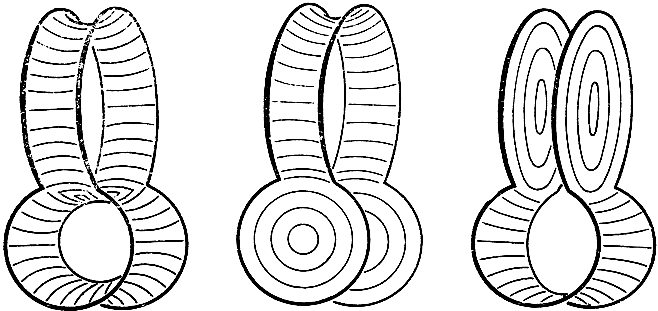
Рис. 244-246. На каркасе натянуты три различные поверхности родов 0 и 1Нетрудно построить более сложные модели в таком же роде и подвергнуть их экспериментальному исследованию.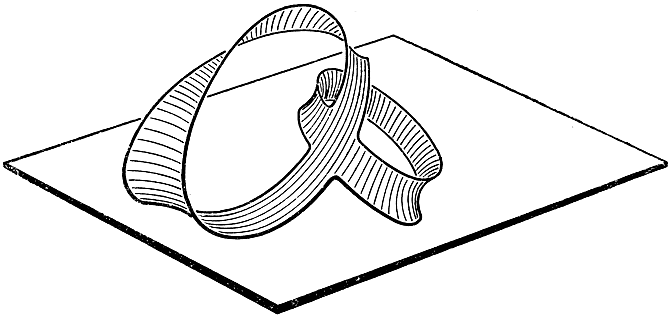
Рис. 247. Односторонняя минимальная поверхность более сложной топологической структуры, натянутая на простой замкнутый контурИнтересное явление - возникновение минимальных поверхностей, ограниченных двумя или большим числом взаимно зацепленных замкнутых контуров. В случае двух круговых контуров получается поверхность, изображенная на рис. 248. Если в этом примере плоскости кругов взаимно перпендикулярны и прямая их пересечения есть общий диаметр двух кругов, то существуют две диаметрально противоположные формы минимальной поверхности с одинаковыми площадями. Представим себе теперь, что два круга постепенно изменяют свое взаимное положение; тогда и форма минимальной поверхности будет меняться непрерывно, хотя при каждом положении кругов только для одной из поверхностей осуществляется абсолютный минимум, для другой же - только относительный. При некоторых положениях поверхность относительного минимума вдруг разрывается и заменяется поверхностью абсолютного минимума. Обе минимальные поверхности в этом примере - одного и того же топологического типа (как и поверхности на рис. 245 и 246).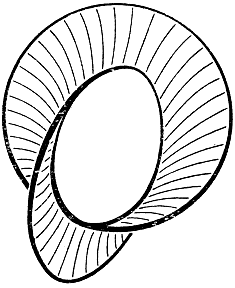
Рис. 248. Поверхность, натянутая на два зацепленных круга
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'