*4. Теорема о неподвижной точке

В приложениях топологии к другим отраслям математики играют важную роль теоремы о "неподвижной точке". Типическим примером является излагаемая ниже теорема Брауэра. Она гораздо менее "очевидна" в интуитивном смысле, чем другие топологические теоремы.

Рассмотрим круглый диск на плоскости. Под таковым мы понимаем внутренность некоторого круга вместе с его границей (окружностью). Предположим, что весь этот диск подвергается некоторому непрерывному преобразованию (даже не обязательно взаимно однозначному), при котором всякая точка диска остается точкой диска, хотя и меняет свое положение. Например, представляя себе этот диск сделанным из тонкой резины, можно его сжимать, растягивать, вращать, изгибать - одним словом, деформировать как угодно, лишь бы его точки не вышли за пределы первоначального положения диска. Иначе еще можно представить себе, что жидкость, налитая в стакан, приведена в движение таким образом, что частицы, находившиеся на поверхности, остаются на ней и во время движения; тогда в каждый определенный момент времени положение частиц на поверхности определяет некоторое непрерывное преобразование первоначального их распределения. Теорема Брауэра утверждает: Каждое непрерывное преобразование такого рода оставляет неподвижной по крайней мере одну точку; другими словами, существует по меньшей мере одна точка, положение которой после преобразования совпадает с положением ее до преобразования. (В примере с жидкостью неподвижные точки зависят от избранного момента временит, в частности, если движение сводится к простому круговому вращению, то неподвижной точкой в любой момент является центр.) Излагаемое далее доказательство существования неподвижной точки - очень характерный пример рассуждений, применяемых в топологии.

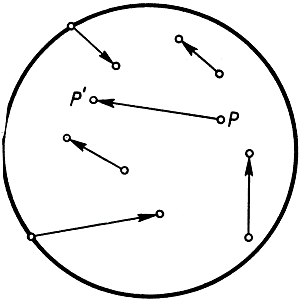
Рис. 132. Векторы преобразования

Рассмотрим наш диск до и после преобразования и допустим, что, вопреки утверждению теоремы, ни одна точка не остается неподвижной, так что любая точка диска после преобразования превращается в некоторую другую точку диска. Каждой точке Р диска в его первоначальном положении сопоставим стрелку или "вектор преобразования" РР', причем Р' есть та точка, в которую переходит Р после преобразования. Такая стрелка будет выходить из каждой точки диска, так как всякая точка куда-то перемещается. Рассмотрим теперь все точки граничной окружности вместе с соответствующими векторами преобразования. Все эти векторы направлены внутрь круга, так как по предположению ни одна точка не выходит за его пределы. Начнем с какой-нибудь точки Р, лежащей на граничной окружности, и пойдем по этой окружности в направлении, противоположном движению часовой стрелки. При этом направление вектора преобразования будет изменяться, так как различным точкам границы соответствуют различно направленные векторы. Все эти векторы можно также представить себе (подвергнув их параллельному переносу) выходящими из некоторой одной и той же точки плоскости (рис. 133). Легко понять, что, когда мы обойдем один раз весь круг от точки Р₁ до точки Р₂, соответствующий вектор после ряда поворотов вернется в первоначальное положение. Число полных поворотов, сделанных при этом нашим вектором, мы назовем индексом рассматриваемой граничной окружности; точнее говоря, мы определим индекс как алгебраическую сумму различных изменений в угле векторов, условливаясь, что всякому частному повороту по часовой стрелке приписывается знак минус, против часовой стрелки - знак плюс. Индекс есть итоговый результат, который a priori равен одному из чисел 0, ±1, ±2, ±3, ..., соответствующих итоговым поворотам на 0°, ±360°, ±720°, ... . Мы утверждаем теперь, что индекс граничной окружности равен единице, т. е. что итоговый поворот вектора преобразования составляет один полный поворот в положительном направлении. Прежде всего напомним еще раз, что вектор преобразования, имеющий начало в точке граничной окружности, направлен непременно внутрь круга, а не по касательной. Если допустим, что итоговый поворот вектора преобразования отличается от итогового поворота касательного вектора (а этот последний поворот в точности равен 360°, так как касательный вектор, очевидно, делает один полный поворот), то разность между итоговыми поворотами касательного вектора и вектора преобразования будет равна кратному 360°, но никак не нулю. Отсюда следует, что вектор преобразования при обходе круга должен будет по крайней мере раз сделать полный поворот вокруг касательного вектора, а так как оба вектора изменяются непрерывно, то в некоторой точке окружности направления обоих векторов совпадут. Но это, как мы видели, невозможно.

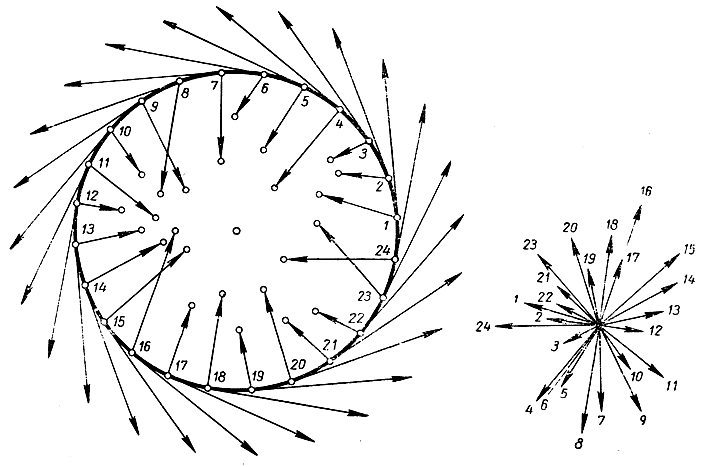
Рис. 133. К доказательству теоремы Брауэра

Рассмотрим теперь окружность, концентрическую границе диска, но с меньшим радиусом, а также соответствующие векторы преобразования. Для этой новой окружности индекс также непременно равен единице. В самом деле, при переходе от граничной окружности к новой окружности индекс должен меняться непрерывно, так как направления самих векторов преобразования меняются непрерывно. Но индекс может принимать только целые значения и потому остается равным единице: действительно, переход от единицы к какому-нибудь другому целому числу обязательно был бы связан со скачком, т. е. нарушением непрерывности. (Очень характерное математическое рассуждение: величина меняется непрерывно, но может принимать только целые значения, значит, она постоянна.) Итак, мы можем найти окружность, концентрическую граничной, притом сколь угодно малую, для которой индекс будет равен единице. Но это невозможно, так как, в силу непрерывности преобразования, векторы преобразования в достаточно малом круге должны весьма мало отличаться от вектора в центре круга. И потому итоговый поворот такого вектора при обходе круга может быть сделан, скажем, меньше 10°, если только радиус круга будет достаточно мал. Но отсюда следует, что индекс такого круга {обязательно целое число) не может быть отличен от нуля. Полученное противоречие показывает, что сделанное нами допущение об отсутствии неподвижных точек преобразования должно быть отвергнуто. Таким образом, теорема доказана.

Теорема о неподвижных точках имеет место не только для кругового диска, но, конечно, и для треугольника, квадрата и всякой другой фигуры, в которую диск может быть переведен топологическим преобразованием. В самом деле, если бы некоторая фигура A, получающаяся из кругового диска посредством такого рода преобразования, могла быть преобразована сама в себя без неподвижных точек, то тем самым было бы определено и топологическое преобразование кругового диска самого в себя без неподвижных точек, а это, как мы видели, невозможно. Теорема обобщается также на случай трехмерных фигур - сфер или кубов, но доказательство здесь уже не столь просто.

^* Хотя теорема Брауэра о неподвижных точках в случае круга не является вполне очевидной в интуитивном смысле, однако легко убедиться, что она является непосредственным следствием такой, достаточно очевидной теоремы: Невозможно непрерывно отобразить круговой диск в одну только его граничную окружность таким образом, чтобы каждая точка этой окружности оставалась неподвижной. Убедимся, что существование непрерывного отображения круга в себя без неподвижных точек противоречит этой последней теореме. Предположим, что указанное рода непрерывное преобразование Р→Р' существует. Тогда для всякой точки Р нашего диска проведем вектор с началом в точке Р', проводя его через Р и заканчивая в точке Р^*, где он встретится с граничной окружностью. Тогда преобразование РР^* будет непрерывным отображением всего диска в граничную окружность, оставляющим неподвижными все точки этой окружности, возможность чего была отвергнута. Подобное рассуждение можно применить и при доказательстве теоремы Брауэра в трехмерном случае сферы или куба.

Легко убедиться, с другой стороны, что для некоторых фигур непрерывные отображения в себя без неподвижных точек возможны.

Например, кольцеобразная область между двумя концентрическими окружностями может быть подвергнута вращению около центра на угол, не являющийся кратным 360°, и это как раз будет непрерывным преобразованием области в себя без неподвижных точек. Такое же преобразование можно произвести над поверхностью сферы, сопоставляя всякой ее точке диаметрально противоположную. Но, применяя тот же метод, что и в случае диска, не представит труда доказать, что непрерывное преобразование сферической поверхности, не переводящее ни одной точки в диаметрально противоположную (например, всякая малая деформация), непременно имеет неподвижные точки.

Теоремы о неподвижных точках вроде перечисленных выше доставляют могущественный метод для доказательства многих "теорем существования" в разных областях математики, причем геометрический характер этих теорем часто далеко не очевиден. Замечательным примером может служить теорема Пуанкаре, высказанная им незадолго до смерти, в 1912 г., без доказательства. Из этой теоремы непосредственно вытекает существование бесчисленного множества периодических орбит в ограниченной проблеме трех тел. Пуанкаре не сумел обосновать своей догадки, доказательство этого замечательного факта получил через год американский математик Г. Д. Биркгоф. С тех пор топологические методы неоднократно и с большим успехом применялись к изучению качественного поведения динамических систем.