1. Классификация геометрических свойств. Инвариантность при преобразованиях

В геометрии рассматриваются свойства фигур на плоскости и в пространстве. Эти свойства столь многочисленны и столь разнообразны, что необходим какой-то принцип классификации для того, чтобы внести порядок в обширное собрание накопленных знаний. Можно было бы, например, положить в основу классификации метод, применяемый при выводе получаемых утверждений. С этой точки зрения обыкновенно различаются "синтетические" и "аналитические" процедуры. Синтетические доказательства существенно связаны с классическим аксиоматическим методом, идущим от Евклида: рассуждение строится на чисто геометрической основе, независимо от средств алгебры и концепции числового континуума, и все теоремы выводятся формально логическим путем, исходя из некоторого числа начальных положений, называемых аксиомами или постулатами. Другой метод подразумевает введение числовой координатной системы и пользуется техническим аппаратом алгебры. Этот метод произвел глубокие изменения в самой математической науке, слив в одно органическое целое геометрию, анализ и алгебру.

В этой главе, однако, нас будет интересовать не столько классификация методов, сколько классификация содержания, то есть сами по себе утверждения теорем, а не способы их доказательства. В элементарной геометрии плоскости резко различаются две группы теорем; в одних идет речь о равенстве фигур, об измерении отрезков и углов, в других - о подобии фигур, для которого существенно измерение углов, но не отрезков. Указанное различие не столь уж существенно, так как длины отрезков и величины углов довольно тесно связаны между собой и разделять их - несколько искусственно. (Изучение этой связи составляет главным образом предмет тригонометрии.) Отметим иную сторону дела. В элементарной геометрии мы имеем дело с величинами: отрезками, углами, площадями. Две фигуры там считаются эквивалентными, если они конгруэнтны, т. е. могут быть переведены одна в другую посредством движения - преобразования, меняющего только положение фигуры, но не числовые значения величин, с ней связанных. Возникает вопрос: является ли значение величин - и вместе с тем конгруэнтность или подобие фигур - чем-то существенно неизменным в геометрии? Или же имеются иные, более глубоко лежащие свойства геометрических фигур, которые сохраняются также и при преобразованиях более общего типа, чем движения? Мы увидим, что такие свойства существуют.

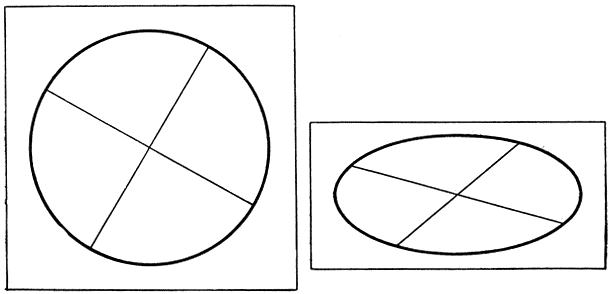
Рис. 69. Сжатие окружности

Представим себе, что на прямоугольной доске, изготовленной из мягкого эластичного материала, нарисован круг с парой взаимно перпендикулярных диаметров (рис. 69). Если мы положим эту доску в тиски и сожмем до половины ее первоначальной ширины, то окружность превратится в эллипс и углы между диаметрами уже не будут прямыми. Окружность обладает тем свойством, что все ее точки находятся на одном и том же расстоянии от центра, но эллипс не обладает таким свойством. Могло бы показаться, что сжатие уничтожает все геометрические свойства первоначальной конфигурации. Но и это предположение далеко от истины: например, утверждение, что центр делит диаметры пополам, одинаково справедливо и для окружности, и для эллипса; в данном случае мы встречаемся с таким свойством фигуры, которое сохраняется при весьма резком изменении в размерах ее отдельных элементов. Сделанные замечания наводят на мысль о возможности классифицировать теоремы, относящиеся к той или иной геометрической фигуре, в зависимости от того, сохраняют ли они силу или теряют ее при равномерном сжатии (или растяжении). Можно поставить и более общий вопрос, исходя из некоторого данного класса преобразований фигуры (такого рода классы, например, порождаются совокупностью всех движений или сжатий, или, скажем, круговых инверсий и т. д.); можно поинтересоваться тем, какие свойства фигуры остаются неизменными, когда фигура подвергается различным преобразованиям данного класса. Система теорем, утверждающих такие свойства, составляет геометрию рассматриваемого класса преобразований. Идея классификации различных отраслей геометрии в соответствии с классами преобразований принадлежит Феликсу Клейну (1849-1925); она была высказана в 1872 г. в его знаменитом выступлении, получившем широкую известность под именем "Эрлангенской программы". С тех пор эта идея оказала решающее влияние на направление многих геометрических исследований.

В главе V мы будем иметь случай установить весьма удивительное обстоятельство, заключающееся в том, что некоторые свойства геометрических фигур заложены настолько глубоко, что не исчезают даже после совершенно произвольных деформаций: так, фигуры, нарисованные на куске резины, не потеряют кое-каких характеристических черт при самых разнообразных и самых резких деформациях. Но в настоящей главе мы займемся теми свойствами, которые сохраняются, "инвариантны" при некотором специальном классе преобразований, более широком, чем весьма ограниченный класс движений, но более узком, чем самый общий класс произвольных деформаций. Мы говорим о классе "проективных преобразований".