3. "Кардинальные числа" Кантора

Резюмируем полученные результаты. Число элементов конечного множества А не может равняться числу элементов другого конечного множества В, если А содержит больше элементов, чем В. Но если мы заменим понятие "множеств, имеющих одно и то же конечное число элементов" более общим понятием "эквивалентных множеств", то в случае бесконечных множеств предыдущее утверждение уже не будет справедливо: множество всех целых чисел содержит "больше" элементов, чем множество всех четных чисел, а множество о всех рациональных чисел - "больше" элементов, чем множество всех целых чисел; и, однако, как мы видели, все эти множества эквивалентны. Можно было бы заподозрить, что все бесконечные множества между собой эквивалентны, но Кантор опроверг это предположение: существует множество - континуум действительных чисел,- которое не эквивалентно никакому счетному множеству.

Итак, существует по меньшей мере два различных "типа бесконечности": счетная бесконечность натуральных чисел и несчетная бесконечность континуума. Если два множества А и В, конечные или бесконечные, эквивалентны, мы скажем, иначе, что им соответствует одно и то же кардинальное число (или мощность). В случае конечных множеств кардинальное число сводится к обыкновенному натуральному числу, но понятие кардинального числа носит более общий характер. Далее, если случится, что множество А эквивалентно некоторому подмножеству (части) множества В, но само В не эквивалентно ни множеству А, ни какой бы то ни было его части, то говорят, следуя Кантору, что множеству В соответствует большее кардинальное число, чем множеству А. Это употребление термина "число" также согласуется с обычным употреблением в случае конечных множеств. Множество целых чисел есть подмножество множества всех действительных чисел, тогда как множество действительных чисел не эквивалентно ни множеству целых чисел, ни какому бы то ни было его подмножеству (оно ни счетное, ни конечное). Значит, по данному определению континууму действительных чисел соответствует большее кардинальное число, чем множеству натуральных чисел.

^* Кантор показал фактически, как можно построить бесконечную последовательность бесконечных множеств, которым соответствуют все большие и большие кардинальные числа. Так как можно исходить из множества натуральных чисел, то достаточно показать, что, каково бы ни было данное множество А, можно построить другое множество В, у которого кардинальное число будет больше чем у А. Вследствие большой общности этой теоремы доказательство ее по неизбежности несколько абстрактно. Множество В мы определяем как множество, элементами которого являются все возможные подмножества множества А. Говоря о "подмножествах" А, мы в данном случае имеем в виду не только "правильные подмножества" А, но не исключаем и самого множества А, а также "пустого" множества О, не содержащего никаких элементов. (Так, если А состоит из трех целых чисел 1, 2, 3, то В содержит 8 различных элементов {1,2,3}, {1,2}, {1,3}, {2,3}, {1}, {2}, {3} и О.) Каждый элемент множества В сам есть множество, состоящее из каких-то элементов множества А: Допустим теперь, что В эквивалентно А или некоторому подмножеству А, т. е. что существует некоторое правило, приводящее во взаимно однозначное соответствие элементы А или некоторого подмножества А со всеми элементами В, т. е. всеми подмножествами А:

где через S_a обозначено то подмножество А, которому соответствует элемент а множества А. Мы придем к противоречию, если укажем некоторый элемент В, т. е. некоторое подмножество Т множества А, которому не может соответствовать никакой элемент а. Чтобы построить подмножество Т, заметим прежде всего, что для всякого элемента х из А существуют две возможности: либо множество S_x, сопоставляемое зависимостью (2) элементу х, содержит элемент х, либо не содержит. Мы определим Т как подмножество А, состоящее из всех таких элементов х, что S не содержит х. Определенное таким образом множество Т отличается от всякого S_a по крайней мере элементом а, так как если S_a содержит а, то Т не содержит а, а если S_a не содержит а, то Т содержит а. Итак, Т не включено в соответствие (2). Это и показывает, что невозможно установить взаимно однозначное соответствие между элементами А (или некоторого подмножества Л) и элементами В. Но соотношение

устанавливает взаимно однозначное соответствие между всеми элементами А и подмножеством В, состоящим из одноэлементных подмножеств А. Значит, по данному выше определению множеству В соответствует большее кардинальное число, чем множеству А.

^*Упражнение. Если множество А содержит n элементов, то определенное выше множество В содержит 2ⁿ элементов. Если А есть множество натуральных чисел, то В эквивалентно континууму действительных чисел, заключенных между 0 и 1. (Указание. Сопоставьте каждому подмножеству А символ, состоящий из последовательности - конечной в первом примере, бесконечной во втором -

где аⁿ = 1 или 0, смотря по тому, принадлежит или не принадлежит n-й элемент А рассматриваемому подмножеству.)

Могло бы показаться легкой задачей построить множество точек, обладающее большим кардинальным числом, чем множество точек единичного отрезка. Казалось бы, что квадрат со стороной 1, как "двумерная" фигура, должен содержать "больше" точек, чем "одномерный" отрезок. Но, как это ни странно, дело обстоит иначе: кардинальное число точек квадрата в точности равно кардинальному числу точек отрезка. Для доказательства достаточно установить взаимно однозначное соответствие между точками квадрата и точками отрезка. Постараемся это сделать.

Если (х, у) есть какая-нибудь точка единичного квадрата, то координаты ее л: и у могут быть представлены в виде десятичных разложений

причем пусть будет условлено (ради избежания всяких сомнений), что, например, число 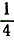будет записываться в виде 0,25000..., а не в виде 0,24999... . Названной точке квадрата (х, у) мы сопоставим точку единичного отрезка

Очевидно, различным точкам квадрата (х, y) и (х', y') сопоставляются различные же точки отрезка z и z'; это и значит, что кардинальное число множества точек квадрата не превышает кардинального числа множества точек отрезка.

(Собственно говоря, в данном случае построено взаимно однозначное соответствие между множеством всех точек квадрата и некоторым подмножеством точек отрезка: никакая точка квадрата не будет соответствовать, например, точке отрезка 0,2140909090..., так как мы условились писать 0,25000..., а не 0,24999... . Но можно слегка видоизменить построение таким образом, чтобы действительно осуществлялось взаимно однозначное соответствие между множеством всех точек квадрата и множеством всех точек отрезка.)

Аналогичное рассуждение показывает, что кардинальное число точек куба не превышает кардинального числа точек отрезка.

Все эти результаты, казалось бы, стоят в противоречии с интуитивным представлением о "размерности". Но нужно обратить внимание на то, что вводимые нами соответствия не являются "непрерывными"; когда мы перемещаемся по отрезку от 0 к 1 непрерывно, соответствующие точки в квадрате не образуют непрерывной кривой, а будут появляться в порядке совершенно "хаотическом". Размерность множества точек зависит не только от кардинального числа точек, но и от того, как они расположены в пространстве. Мы вернемся к этому вопросу в главе V.