с. Теорема о распределении простых чисел

В исследованиях, связанных с законом распределения простых чисел, решительный шаг был сделан тогда, когда математики отказались от тщетных попыток найти элементарную математическую формулу, которая давала бы все простые числа или же точное число простых чисел, содержащихся среди n первых натуральных чисел, и сосредоточили вместо того внимание на распределении в среднем простых чисел среди всех натуральных.

При всяком целом n обозначим через А_n число простых чисел среди чисел 1, 2, 3, ..., n. Если мы выделим среди первых чисел натурального ряда

те, которые являются простыми, то не представит труда подсчитать ряд значений А_n:

Возьмем теперь какую-нибудь неограниченно возрастающую последовательность значений n, например

тогда соответствующие значения А_n:

- также будут возрастать безгранично (хотя и более медленно). Действительно, множество простых чисел, как мы уже знаем, бесконечно, и потому значения А_n рано или поздно станут больше любого назначенного числа. "Плотность" распределения простых чисел среди n первых чисел натурального ряда дается отношением 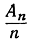; не представляет особого труда с помощью таблиц простых чисел подсчитать значения 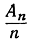при достаточно больших значениях n:

Последняя, скажем, из выписанных строчек в приведенной табличке дает вероятность того, что число, случайно выхваченное из 10⁹ первых чисел натурального ряда, окажется простым: всего имеется 10⁹ возможных выборов, из них A_10⁹ соответствуют простым числам.

Распределение отдельных простых чисел отличается чрезвычайно неправильным характером. Но эта неправильность "в малом" исчезает, если мы направим внимание к распределению "в среднем", находящему 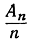свое выражение в изменениях отношения - при неограниченно растущем n. Простой закон, которому подчиняется поведение этого отношения, следует отнести к числу самых замечательных открытий, сделанных во всей математике. Для того чтобы сформулировать теорему о распределении простых чисел, к которой мы теперь подходим, необходимо предварительно разъяснить, что такое "натуральный логарифм" числа n. Для этой цели возьмем в плоскости две взаимно перпендикулярные оси и рассмотрим геометрическое место таких точек на плоскости, для которых произведение расстояний х и у от двух осей равно единице. На координатном языке это геометрическое место есть равносторонняя гипербола, уравнение которой имеет вид ху = 1. Мы определим ln n как площадь (рис. 5) фигуры, ограниченной гиперболой и двумя вертикальными прямыми х = 1 и х = n. (Более детально логарифм и его свойства будут рассмотрены в главе VIII.) Чисто случайно, в связи с изучением таблицы простых чисел, Гаусс заметил, что отношение 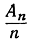приблизительно равно 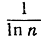и что точность этого приближения, по-видимому, улучшается при возрастании n. Насколько удовлетворительно приближение, можно судить по отношению 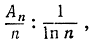значения которого при n = 1000, 1 000 000, 1 000 000 000 показаны в следующей табличке:

Основываясь на такого рода эмпирической очевидности, Гаусс высказал в качестве предположения, что отношение 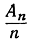"асимптотически равно" 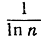. Смысл этого утверждения заключается в следующем: если возьмем последовательность значений n, становящихся все больше и больше, например,

(как мы делали и раньше), то отношение

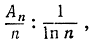
вычисляемое для этих последовательно рассматриваемых значений n, будет становиться все более и более близким к числу 1, а именно разность между указанным отношением и единицей будет делаться столь малой, сколь будет назначено, лишь бы только мы рассматривали достаточно большие значения n. Такого рода соотношение символически выражается знаком ~: выражение 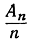~ 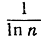означает, что 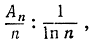при возрастании n стремится к 1. Что знак ~ не может быть заменен знаком обыкновенного равенства (=), ясно хотя бы из того факта, что А_n - непременно целое число, тогда как 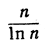не является таковым.

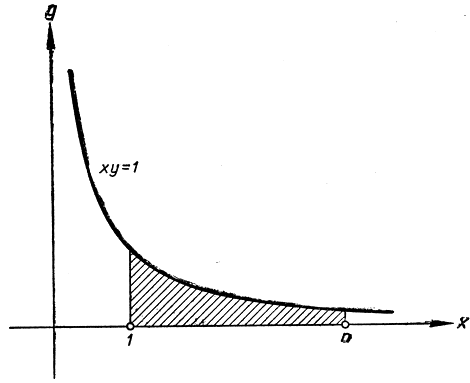
Рис. 5. Площадь заштрихованной области под гиперболой определяет функцию ln n

То обстоятельство, что распределение простых чисел хорошо описывается с помощью логарифмической функции, нельзя не признать поистине поразительным, так как здесь вступают в тесное соприкосновение два математических понятия, казалось бы, не имеющие друг к другу никакого отношения.

Хотя схватить содержание высказанного Гауссом предположения не представляет особой трудности, однако его строгое математическое доказательство во времена Гаусса было за пределами возможностей математической науки. Для того чтобы доказать теорему о распределении простых чисел, говорящую лишь о самых элементарных математических понятиях, неизбежно нужно прибегнуть к самым мощным методам современной математики. Пришлось ждать почти сто лет, пока анализ получил достаточное развитие для того, чтобы Адамар (1896) в Париже и Валле-Пуссен (1896) в Лувэне смогли дать исчерпывающее доказательство теоремы о распределении простых чисел. Упрощения и важные дополнения были затем внесены Мангольдтом и Э. Ландау. Задолго до Адамара значительное продвижение в этой области было сделано Риманом (1826-1866) в его знаменитой работе, намечающей основные стратегические линии предстоящей атаки. Совсем недавно американский математик Норберт Винер сумел видоизменить доказательство таким образом, чтобы избежать применения комплексных чисел в узловых моментах проводимых рассуждений. Но все же доказательство теоремы о распределении простых чисел остается слишком сложным для того, чтобы его можно было предложить начинающему. Мы вернемся к этому вопросу на стр. 521 и следующих.