
5. Алгебра матриц
Большую роль в линейной алгебре и многих других областях математики играют так называемые матрицы.
Под матрицей понимают прямоугольную таблицу вида

где буквы aij обозначают некоторые элементы. Эти обозначения содержат два индекса, первый из которых указывает номер строки, а второй номер столбца, на пересечении которых находится соответствующий элемент. Про матрицу, у которой m строк и n столбцов, говорят, что она имеет порядок m × n. В случае, когда число строк и столбцов одинаково (m = n), матрица называется квадратной порядка n.
Если m = 1, то матрицу можно понимать как вектор, координаты которого записаны в строку; ее тогда так и называют вектор-строка. Точно так же в случае одностолбцовой матрицы пользуются термином вектор-столбец. Иногда матрицу обозначают одной буквой (А, В и т. д.), а вместо (1) часто используется сокращенное обозначение (aij).
Если в исходной матрице А строки и столбцы поменять ролями, то получим матрицу, называемую транспонированной к А (обозначается AT). Матрица, транспонированная к матрице (1), имеет вид:
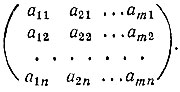
Для матриц с действительными элементами определяются операции сложения матриц и умножения матрицы на число, аналогичные кооперациям над векторами, а именно, для любых двух матриц порядка m × n
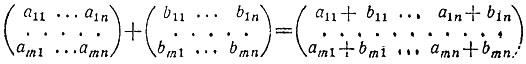
и для любой матрицы и любого числа α
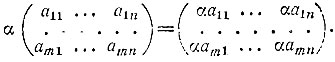
Определение этих операций выглядит вполне естественно. Иначе обстоит дело с довольно своеобразной операцией умножения матриц. Рассмотрим сначала умножение квадратных матриц одного порядка n. Если
А = (аij) и B = (bij)
- две таких матрицы, то их произведением
С = А · В = (сij)
называется квадратная матрица порядка n, произвольный элемент которой вычисляется по правилу:
сij = аi1b1j + аi2b2j + ... + аinbnj. (2)
Иначе говоря, чтобы получить элемент i-й строки и j-го столбца матрицы С = А · В, нужно взять сумму произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В. Например,
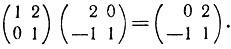
Умножение матриц некоммутативно, т. е., вообще говоря, А · B ≠ В · А. Так, перемножив две предыдущие матрицы в обратном порядке, получим иную матрицу:
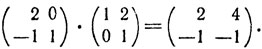
Вместе с тем, нетрудно доказать, что умножение матриц ассоциативно:
(А · В) · С = А · (В · С).
Особую роль (подобную числовой единице) играет так называемая единичная матрица
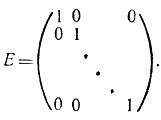
Действительно, из формулы (2) следует, что
ЕА = АЕ = А
для любой квадратной матрицы А.
Можно убедиться, что множество всех квадратных матриц заданного порядка образует относительно введенных операций сложения и умножения (некоммутативное) кольцо.
Правило умножения матриц можно распространить и на прямоугольные матрицы, не являющиеся квадратными. Формула (2) позволяет это сделать, если число столбцов первой матрицы А совпадает с числом строк матрицы В. Например,
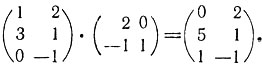
При этом получающаяся матрица имеет столько же строк, сколько первый сомножитель, и столько же столбцов, сколько второй. Пользуясь операциями над матрицами, мы получаем возможность записывать произвольные системы уравнений в краткой матричной форме, Действительно, пусть матрица
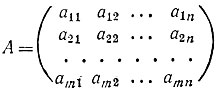
составлена из коэффициентов при неизвестных системы (1) приложения 4 (в этом случае она называется матрицей системы). Рассмотрим векторы-столбцы неизвестных и свободных членов, обозначая их соответственно через х и b:
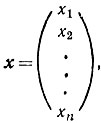
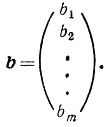
Тогда произведение Ах есть матрица с m строками и одним столбцом, т. е. вектор-столбец, элементы которого вычисляются согласно формуле (2). Таким образом,
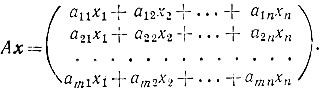
Каждое из уравнений системы (1) означает равенство соответствующих координат вектора Ах и вектора b, и вся система в целом означает тогда равенство
Ах = b.
Полученная краткая запись и есть матричная форма системы линейных уравнений. Подобная матричная запись встречается во множестве других ситуаций, и она широко используется в математической, физической и технической литературе.
Все сказанное о матрицах с действительными элементами в равной мере относится к матрицам с элементами из произвольного поля F. Так, в теории кодирования приходится рассматривать матрицы, составленные из элементов конечного поля. Естественно, что при оперировании с такими матрицами их элементы складываются и умножаются в соответствии с "арифметикой" поля F. Вот, к примеру, как перемножаются две матрицы с элементами из Z2:
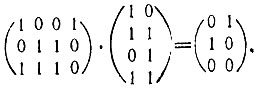
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'