
4. Арифметическое n-мерное векторное пространство
Всякая точка на плоскости при выбранной системе координат задается парой (α, β) своих координат; числа α и β можно понимать также как координаты радиуса-вектора с концом в этой точке. Аналогично, в пространстве тройка (α, β, γ) определяет точку или вектор с координатами α, β, γ. Именно на этом основывается хорошо известная читателю геометрическая интерпретация систем линейных уравнений с двумя или тремя неизвестными. Так, в случае системы двух линейных уравнений с двумя неизвестными
а1х + b1у = с1,
а2х + b2у = с2
каждое из уравнений истолковывается как прямая на плоскости (см. рис. 26), а решение (α, β) - как точка пересечения этих прямых или как вектор с координатами аир (рисунок соответствует случаю, когда система имеет единственное решение).
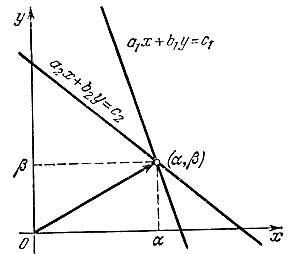
Рис. 26
Аналогично можно поступить с системой линейных уравнений с тремя неизвестными, интерпретируя каждое уравнение как уравнение плоскости в пространстве.
В математике и различных ее приложениях (в частности, в теории кодирования) приходится иметь дело с системами линейных уравнений, содержащих более трех неизвестных. Системой линейных уравнений с n неизвестными x1, х2, ..., хn называется совокупность уравнений вида
а11х1 + а12х2 + ... + а1nхn = b1,
а21х1 + а22х2 + ... + а2nхn = b2,
. . . . . . . . . . . . . . . . . . . . . . (1)
аm1х1 + аm2х2 + ... + аmnхn = bm,
где aij и bi - произвольные действительные числа. Число уравнений в системе может быть любым и никак не связано с числом неизвестных. Коэффициенты при неизвестных аij имеют двойную нумерацию: первый индекс i указывает номер уравнения, второй индекс j - номер неизвестного, при котором стоит данный коэффициент. Всякое решение системы понимается как набор (действительных) значений неизвестных (α1, α2, ..., αn), обращающих каждое уравнение в верное равенство.
Хотя непосредственное геометрическое истолкование системы (1) при n > 3 уже невозможно, однако вполне возможно и во многих отношениях удобно распространить на случай произвольного n геометрический язык пространства двух или трех измерений. Этой цели и служат дальнейшие определения.
Всякий упорядоченный набор из n действительных чисел (α1, α2, ..., αn) называется n-мерным арифметическим вектором, а сами числа α1, α2, ..., αn - координатами этого вектора.
Для обозначения векторов используется, как правило, жирный шрифт и для вектора а с координатами α1, α2, ..., αn сохраняется обычная форма записи:
а = (α1, α2, ..., αn).
По аналогии с обычной плоскостью множество всех n-мерных векторов, удовлетворяющих линейному уравнению с n неизвестными, называют гиперплоскостью в n-мерном пространстве. При таком определении множество всех решений системы (1) есть не что иное, как пересечение нескольких гиперплоскостей.
Сложение и умножение n-мерных векторов определяются по тем же правилам, что и для обычных векторов. А именно, если
а = (α1, α2, ..., αn), b = (β1, β2, ..., βn) (2)
- два n-мерных вектора, то их суммой называется вектор
α + β = (α1 + β1, α2 + β2, ..., αn + βn). (3)
Произведением вектора а на число λ называется вектор
λа = (λα1, λα2, ..., λαn). (4)
Множество всех n-мерных арифметических векторов с операциями сложения векторов и умножения вектора на число называется арифметическим n-мерным векторным пространством Ln.
Используя введенные операции, можно рассматривать произвольные линейные комбинации нескольких векторов, т. е. выражения вида
λ1a1 + λ2a2 + ... + λkak,
где λi - действительные числа. Например, линейная комбинация векторов (2) с коэффициентами λ и μ - это вектор
λа + μb = (λα1 + μβ1, λα2 + μβ2, ..., λαn + μβn).
В трехмерном пространстве векторов особую роль играет тройка векторов i, j, k (координатные орты), по которым разлагается любой вектор а:
a = xi + yj + zk,
где х, у, z - действительные числа (координаты вектора а).
В n-мерном случае такую же роль играет следующая система векторов:
e1 = (1, 0, 0, ..., 0),
e2 = (0, 1, 0, ..., 0),
e3 = (0, 0, 1, ..., 0),
. . . . . . . . . . . . (5)
en = (0, 0, 0, ..., 1).
Всякий вектор а есть, очевидно, линейная комбинация векторов е1, e2, ..., en:
а = а1е1 + а2е2 + ... + аnеn, (6)
причем коэффициенты α1, α2, ..., αn совпадают с координатами вектора а.
Обозначая через 0 вектор, все координаты которого равны нулю (кратко, нулевой вектор), введем следующее важное определение:
Система векторов а1, а2, ..., аk называется линейно зависимой, если существует равная нулевому вектору линейная комбинация
λ1a1 + λ2a2 + ... + λkak = 0,
в которой хотя бы один из коэффициентов h1, λ2, ..., λk отличен от нуля. В противном случае система называется линейно независимой.
Так, векторы
а1 = (1, 0, 1, 1), а2 = (1, 2, 1, 1), а3 = (2, 2, 2, 2)
линейно зависимы, поскольку
a1 + a2 - а3 = 0.
Линейная зависимость, как видно из определения, равносильна (при k ≥ 2) тому, что хотя бы один из векторов системы является линейной комбинацией остальных.
Если система состоит из двух векторов a1, а2, то линейная зависимость системы означает, что один из векторов пропорционален другому, скажем, а1 = λа2; в трехмерном случае это равносильно коллинеарности векторов а1 и а2. Точно так же линейная зависимость системы I из трех векторов в обычном пространстве означает компланарность этих векторов. Понятие линейной зависимости является, таким образом, естественным обобщением понятий коллинеарности и компланарности.
Нетрудно убедиться, что векторы е1, е2, ..., еn из системы (5) линейно независимы. Следовательно, в n-мерном пространстве существуют системы из n линейно независимых векторов. Можно показать, что всякая система из большего числа векторов линейно зависима.
Всякая система a1, а2, ..., аn из n линейно независимых векторов n-мерного пространства Ln называется его базисом.
Любой вектор а пространства Ln раскладывается, и притом единственным образом, по векторам произвольного базиса a1, а2, ..., аn:
а = λ1a1 + λ2a2 + ... + λnan.
Этот факт легко устанавливается на основании определения базиса.
Продолжая аналогию с трехмерным пространством, можно и в n-мерном случае определить скалярное произведение а · b векторов, полагая
a · b = α1β1 + α2β2 + ... + αnβn.
При таком определении сохраняются все основные свойства скалярного произведения трехмерных векторов. Векторы а и b называются ортогональными, если их скалярное произведение равно нулю:
α1β1 + α2β2 + ... + αnβn = 0.
В теории линейных кодов используется еще одно важное понятие - понятие подпространства. Подмножество V пространства Ln называется подпространством этого пространства, если
1) для любых векторов а, b, принадлежащих V, их сумма а + b также принадлежит V;
2) для любого вектора а, принадлежащего V, и для любого действительного числа λ вектор λа также принадлежит V.
Например, множество всех линейных комбинаций векторов e1, е2 из системы (5) будет подпространством пространства Ln.
В линейной алгебре доказывается, что во всяком подпространстве V существует такая линейно независимая система векторов a1, a2, ..., ak, что всякий вектор а подпространства является линейной комбинацией этих векторов:
a = λ1a1 + λ2a2 + ... + λkak.
Указанная система векторов называется базисом подпространства V.
Из определения пространства и подпространства непосредственно следует, что пространство Ln есть коммутативная группа относительно операции сложения векторов, а любое его подпространство V является подгруппой этой группы. В этом смысле можно, например, рассматривать смежные классы пространства Ln по подпространству V.
В заключение подчеркнем, что если в теории n-мерного арифметического пространства вместо действительных чисел (т. е. элементов поля действительных чисел) рассматривать элементы произвольного поля F, то все определения и факты, приведенные выше, сохранили бы силу.
В теории кодирования важную роль играет случай, когда поле F поле вычетов Zp, которое, как мы знаем, конечно. В этом случае соответствующее n-мерное пространство также конечно и содержит, как нетрудно видеть, рn элементов.
Понятие пространства, как и понятия группы и кольца, допускает также и аксиоматическое определение. За подробностями мы отсылаем Питателя к любому курсу линейной алгебры.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'