
19. Латинские квадраты и коды
Латинские квадраты долгое время были известны лишь математикам и любителям головоломок и, в основном, благодаря одной знаменитой задаче Л. Эйлера *). В 1782 г. Эйлер предложил следующую проблему.
*) (Леонард Эйлер (1707-1783) - один из великих математиков XVIII века, создавших основы математического анализа. Швейцарец по происхождению, он жил и работал преимущественно в России. Эйлер, выделявшийся своей исключительной интуицией и разносторонностью интересов, оставил глубокий след практически во всех областях современной ему математики. Большое количество его замечательных результатов явилось основой для дальнейшего развития многих разделов математики.)
Среди 36 офицеров находится по шесть офицеров шести различных званий из шести полков. Можно ли построить этих офицеров в каре так, чтобы в каждой колонне и каждой шеренге встречались офицеры всех званий и всех полков?
Лишь в 1901 г. удалось доказать, что это невозможно. Однако связанные с задачей Эйлера латинские квадраты не потеряли интереса, так как вскоре обнаружилось, что они имеют многообразные практические применения. А совсем недавно (конец шестидесятых годов) они были применены и в теории кодирования. Получающиеся на их основе коды, хотя и далеки по своим параметрам от оптимальных, но зато допускают простые алгоритмы декодирования (голосование в один шаг).
Будем рассматривать квадратные матрицы порядка я, элементы которых - числа 1, 2, ..., n. Такую матрицу называют латинским квадратом, если всякий элемент входит ровно один раз в каждую строку и в каждый столбец.
Следующие матрицы являются примерами латинских квадратов (соответственно порядка 2, 3 и 4):
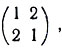
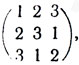

Существенным при построении кодов является свойство ортогональности матриц, которое определяется следующим образом.
Две матрицы порядка n называются ортогональными (не путать с ортогональностью векторов!), если при наложении любой из них на другую мы получим множество всех упорядоченных пар (i, j), l ≤ i ≤ n, 1 ≤ j ≤ n. Вот пример ортогональных латинских квадратов порядка 3:

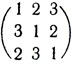
Ортогональны также и следующие две матрицы;
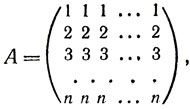

Легко видеть, что матрица порядка n является латинским квадратом тогда и только тогда, когда она ортогональна обеим матрицам A и В.
При построении кодов используются матрицы (1) и им ортогональные. Способ построения обеспечивает нужное для декодирования число ортогональных проверок; состоит этот способ в следующем.
Для матрицы С указанного типа и для любого ее элемента k определим двоичную матрицу Ck, которая получается из С заменой всех элементов, равных k, единицами, а всех остальных элементов - нулями. Таким образом, по матрице С порядка n строятся матрицы С1, С2, ..., Сn. Каждой из этих матриц Ck сопоставим вектор υk, первые n координат которого являются последовательными элементами первой строки матрицы Ck, следующие n координат - элементами второй строки и т. д. Иными словами, n2 координат вектора υk - это все элементы матрицы Ck, "вытянутой" в одну общую строку. Образуем, наконец, матрицу С˜ порядка n × n2, строками которой являются векторы υk:
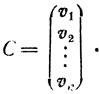
Например, для матрицы
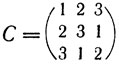
имеем:
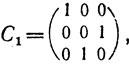
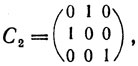
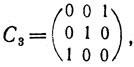
υ1 = (100001010), υ2 = (010100001), υ3 = (001010100),

Пусть теперь А и В - матрицы (1), a D1, D2, ...,Dr - попарно ортогональные латинские квадраты. Образуем из них указанным выше способом матрицы A˜, В˜, D˜1, D˜2, ..., D˜r, а затем построим матрицу H, которую можно условно представить в виде:
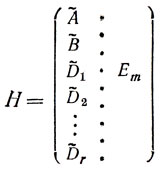
(матрицы A˜, В˜, D˜1, D˜2, ..., D˜r подписываются одна под другой и к получившейся матрице приписывается справа единичная матрица Еm соответствующего порядка m).
Матрицу Н будем считать проверочной матрицей кода, построенного с помощью латинских квадратов. Число строк этой матрицы, как вытекает из построения, равно (r + 2)n, а число столбцов составляет n2 + (r + 2)n. Кодовое расстояние полученного кода, как мы увидим, будет не меньше r + 3.
В качестве примера рассмотрим код, построенный с помощью двух ортогональных латинских квадратов порядка 3:
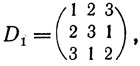
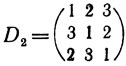
В этом случае
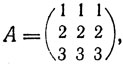
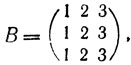




Наконец, проверочная матрица искомого кода такова:

Легко видеть, что для каждого из 9 информационных символов может быть составлено четыре ортогональных проверки. Например, первая, четвертая, седьмая и десятая строки матрицы Н дают следующие проверки для первого символа α0:
α0 = α1 + α2 + α9,
α0 = α3 + α6 + α12,
α0 = α5 + α7 + α15,
α0 = α4 + α8 + α18.
Ортогональность этих соотношений, как можно убедиться, как раз и объясняется свойством ортогональности исходных матриц. При этом число таких соотношений для каждого символа всегда равно числу матриц, используемых для построения, т. е. r + 2. А значит, кодовое расстояние не может быть меньше, чем r + 3; в нашем примере оно не меньше пяти.
На рис. 25 мы приводим часть декодирующей схемы, предназначенную для декодирования символа α0 (буквой М, как и раньше, обозначен мажоритарный элемент).
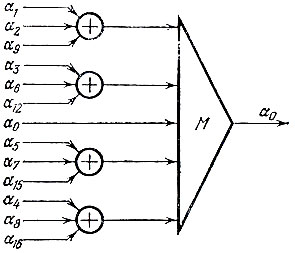
Рис. 25
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'