Задачи и дополнения

1. В теории циклических кодов многочлены удобно трактовать не только как элементы кольца F_n, но и как элементы кольца многочленов F[X] с обычной операцией умножения многочленов. Условимся в последнем случае вместо обозначения а(х) пользоваться обозначением а(Х). Необходимость различать эти обозначения видна хотя бы из такого примера: если в кольце F_n имеет место хⁿ - 1 = 0, то в кольце F[X] многочлен Хⁿ - 1, разумеется, не является нулевым элементом.

Для циклических кодов существенно следующее свойство порождающего многочлена g(x):

Если в качестве g(x) выбран многочлен наименьшей степени, принадлежащий идеалу V, то многочлен g(X) ∈ F[X] является делителем многочлена Хⁿ - 1.

Для доказательства разделим Хⁿ - 1 на g(X) с остатком. Получаем:

где степень r(Х) меньше степени g(X). В кольце F_n равенство (10) приобретает вид:

откуда заключаем, что r(х) должен принадлежать идеалу V, в то время как его степень меньше, чем степень g(x). Следовательно, r(х) = 0, но тогда и r(Х) = 0, т. е.

Многочлен h(Х), удовлетворяющий равенству (11), называется проверочным многочленом.

2. Воспользуемся определением проверочного многочлена для построения проверочной матрицы циклического кода.

Пусть h(x) = ∑^k_j=0 h_jx^j - проверочный многочлен кода. Из (11) следует, что если m - степень многочлена g(x), то h(x) имеет степень n-m, т. е. k = n - m. В силу (11) имеем также, что в кольце F_n проверочный и порождающий многочлены связаны равенством

Рассмотрим матрицу Н порядка m × n, имеющую следующий вид:

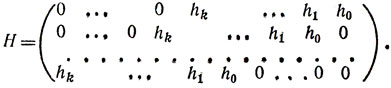
Первая строка этой матрицы составлена из коэффициентов многочлена h(х), записанных в обратном порядке (т. е. в порядке убывания степеней). Последующие строки составлены аналогичным образом из коэффициентов многочленов хh(х), ..., x^m-1h(x).

Докажем, что матрица H является проверочной.

Действительно, пусть а(x) = ∑^n-1_i=0 a_ixⁱ - произвольный кодовый многочлен. Рассмотрим идеал V^g(h(x)), порожденный проверочным многочленом h(х) и возьмем произвольный многочлен: b(х) = ∑^n-1_j=0 b_jx^j из этого идеала. Тогда a(x) = s(x)g(x), b(x) = q(x)h(x) и согласно (12)

С другой стороны, умножая многочлены а(х) и b(х) по правилам умножения в F_n (см. равенства (4)), получаем:

Так как многочлен а(х)Ьb(х) нулевой, то и все его коэффициенты равны нулю, в частности

Это равенство означает, что всякий кодовый вектор ортогонален вектору (b_n-1, b_n-2, ..., b₀) который получается из произвольного многочлена b(x) ∈ V, если его коэффициенты записать в обратном порядке. Таким образом, в силу построения матрицы (13), каждая ее строка ортогональна любому кодовому вектору и, стало быть, эта матрица является проверочной.

3. Вернемся снова к примеру циклического (7,4)-кода с порождающим многочленом g(x) = 1 + x² + x³. Как было доказано, многочлен g(X) = 1 + X² + X³ является делителем многочлена X⁷-1. Легко проверить, что

Следовательно, для проверочного многочлена h(x) имеем:

Поэтому проверочной будет следующая матрица:

4. Исходя из равенств

найти порождающие и проверочные матрицы всех двоичных циклических кодов длины 9 и длины 15.

5. Пусть f(X) = f₀ + f₁X + ... + f_kX^k - произвольный многочлен степени k. Многочлен f^*(X) = X^kf(1/X) называют двойственным к f(Х).

Показать, что проверочная матрица циклического кода может быть записана в виде:

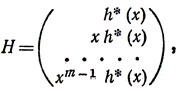
где h^*(х) - многочлен, двойственный к проверочному многочлену h(x).

6. Убедиться, что код, дуальный к циклическому (см. § 11, дополнение 11), также является циклическим. Как связаны между собой порождающие и проверочные многочлены двух дуальных кодов?

7. Пусть g^*(х) - многочлен, двойственный к многочлену g(x). Показать, что

а) коды, порожденные многочленами g(x) и g^*(x), эквивалентны;

б) если для кода с порождающим многочленом g(x) выполняется условие g(x) = g^*(x), то кодовое подпространство такого кода вместе с каждым вектором υ = (а₀, а₁, ..., a_n-1) содержит также и вектор υ^* = (а_n-1, а_n-2, ..., a₀).

8. Среди циклических кодов особую практическую важность имеет один специальный класс кодов, предложенных американскими математиками Боузом, Чоудхури и Хоквингемом. Эти коды так и называются кодами БЧХ - по начальным буквам фамилий этих математиков. Теория кодов БЧХ выходит за рамки настоящей книги, и мы только объясним в нескольких словах, каким образом они определяются. Для этого нам потребуются некоторые дополнительные сведения из теории полей.

Будем говорить, что подмножество F является подполем поля F‾, если F есть поле относительно операций на F‾. Справедлива такая теорема:

Для любого конечного поля F можно указать конечное поле F‾, удовлетворяющее следующим условиям:

3) не существует поля, обладающего свойствами 1 и 2 и имеющего меньше элементов, чем F‾.

Пусть теперь для поля F указано поле F‾ со свойствами 1) - 3). Пусть α - примитивный элемент поля F‾, а числа s и l таковы, что элемент α^s имеет порядок n и s + l < q, где q - число элементов поля F<. Циклический код называется кодом БЧХ (с параметрами n, s, l), если он состоит из всех многочленов степени ≤ n-1 с коэффициентами из F, среди корней которых содержатся все элементы

Можно доказать, что кодовое расстояние такого кода не меньше l + 2. Следовательно, варьируя параметры n, s, l, мы имеем возможность получать коды БЧХ с любым расстоянием, а значит, исправляющие любое заданное число ошибок. Это обстоятельство счастливо дополняется тем, что для указанных кодов разработаны удобные алгоритмы декодирования, основанные на вычислениях в конечных полях и легко реализуемые автоматическими электронными устройствами.

9. До сих пор мы говорили о кодовом расстоянии кода и максимальном числе t исправляемых ошибок как об основных показателях корректирующей способности кода. Однако ясно, что более весомым показателем является величина t/n, показывающая, какова доля числа ошибочных символов от общего числа символов принятого слова, при которой возможно еще правильное декодирование (исправление ошибок). С другой стороны, отношение k/n (k - число информационных символов) характеризует избыточность кода: чем меньше это отношение, тем, очевидно, больше избыточность.

И вот здесь коды БЧХ обнаруживают некоторый изъян. Оказывается, при заданной корректирующей способности, т, е. заданной величине t/n, коды БЧХ большой длины имеют слишком высокую избыточность. Более того: если отношение t/n фиксировано, а n → ∞, то k/n → 0.

Стремление исправить этот недостаток привело к появлению таких кодовых конструкций, как коды-произведения (см. дополнение 12 к § 11) и их обобщение - каскадные коды. Строящиеся, как правило, на базе кодов БЧХ, они в значительной степени сохраняют их достоинства, но одновременно избавлены от упомянутого выше дефекта.