
14. Циклические коды
Среди линейных кодов особо важную роль играют так называемые циклические коды. По ряду причин они являются наиболее ценным достоянием теории кодирования. Во-первых, они допускают еще более компактное описание, чем произвольные линейные коды. Во-вторых, имеющиеся для линейных кодов алгоритмы кодирования и декодирования могут быть в применении к циклическим кодам значительно упрощены; более того, для циклических кодов существуют свои особые методы декодирования, неприложимые к другим линейным кодам. Наконец, по своей структуре эти коды идеально приспособлены к реализации в современных технических устройствах.
Простые в реализации, они, однако, не столь просты в теории. Для полного разъяснения большинства вопросов, связанных с построением и методами декодирования циклических кодов, требуется довольно сложный алгебраический аппарат. Поэтому наше предстоящее знакомство с циклическими кодами будет далеко не полным.
Начнем с понятия циклического сдвига вектора. Пусть задан произвольный n-мерный вектор а = (а0, a1, а2, ..., an-1) с координатами из любого поля F (нумерацию координат в случае циклических кодов удобно начинать с нуля). Циклическим сдвигом этого вектора назовем вектор а' = (аn-1, a0, а1, а2, ..., an-2). Например, для вектора (01101) последовательными циклическими сдвигами являются такие вектора:
(10110), (01011), (10101), (11010).
Циклическим кодом называется линейный код, который вместе с любым своим вектором содержит также и его циклический сдвиг. Иными словами, циклический код обладает следующим свойством: циклический сдвиг любого кодового вектора снова является кодовым вектором.
Циклическим является, например, код с порождающей матрицей
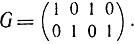
Менее тривиальным примером циклического кода (проверка предоставляется читателю) является код, эквивалентный (7,4)-коду Хемминга, с проверочной матрицей

При рассмотрении циклических кодов кроме обычных действий над векторами мы имеем дело фактически еще с одной операцией, сопоставляющей каждому вектору его циклический сдвиг. Удобным алгебраическим средством для , ее описания являются многочлены. С каждым вектором а = (a0, а1, ..., an-1) свяжем многочлен а(х) = а0 + а1х + ... + an-1xn-1, коэффициенты которого совпадают с соответствующими координатами вектора. В дальнейшем будем отождествлять вектор а с соответствующим ему многочленом а(х), свободно переходя от векторной записи к записи в виде многочлена. Циклическому сдвигу a' = (an-1, a0, a1 ..., an-2) вектора а соответствует тогда многочлен а'(х) = an-1, a0x + a1x2 + ... + an-2xn-1. Сравним многочлены а(х) и а'(х). Если сумму первых n-1 слагаемых а(х) умножить на x, мы получим сумму последних n-1 слагаемых многочлена а'(х). Вообще, нетрудно заметить, что
а'(х) = ха(х) - аn-1(хn - 1). (2)
Будем теперь считать, что х - образующий элемент циклической группы порядка n. Тогда n-я степень х равна единице:
xn = 1, (3)
а все меньшие степени, 1, х, х2, ..., хn-1, являются различными элементами. При этом правило умножения степеней х следующее:
xkxm = xr, (4)
где r ≡ k + m (mod n) и 0 ≤ r < n. С учетом (3) равенство (2) дает:
а'(х) = ха(х),
т. е. циклический сдвиг любого вектора получается умножением этого вектора на х.
Из равенств (3) и (4) вытекает следующее правило умножения любых двух многочленов от х степени ≤ n-1. Если
а(х) = а0 + а1х + ... + аn-1хn-1
и
b(x) = b0 + b1x + ... + bn-1xn-1
- два таких многочлена, то чтобы найти их произведение, сначала обычным образом раскрываем скобки, умножая степени хk и хm по правилу (4), а коэффициенты ak и bm - по правилу умножения в поле F, после чего приводим подобные члены.
Пример 1. Пусть n = 5 и а(х) = 1 + х + х2 + х4 и b(х) = 1 + х3 + х4 - двоичные многочлены. Тогда
a(x)b(x) = (1 + x + x2 + x4)(1 + x3 + x4) = 1 + x + x2 + x4 + x3 + xx3 + x2x3 + x4x3 + x4 + xx4 + x2x4 + x4x4 = 1 + х + х2 + х4 + х3 + х4 + 1 + х2 + х4 + 1 + х + х3 = 1 + х4.
Пример 2. Пусть n = 4, a(x)=1 + 2x + x2 и b(x)= 2 + х + х3 - многочлены над полем Z3. Имеем:
a(x)b(x) = (1 + 2x + x2)(2 + x + x3) = 2 + 2 · 2х + 2х2 + х + 2х2 + х3 + х3 + 2хх3 + х2х3 = 2 + х + 2х2 + х + 2х2 + 2х3 + 2 + х = 1 + х2 + 2х3.
Итак, для многочленов кроме операции сложения определена также и операция умножения (напомним, что сложение многочленов не нуждалось в специальном определении, поскольку многочлены понимаются нами как векторы). При этом, очевидно, операция умножения многочленов коммутативна, ассоциативна и дистрибутивна относительно операции сложения. Поэтому множество Fn всех многочленов степени ≤ n образует относительно указанных операций кольцо. Но тогда циклический код может быть описан в чисто алгебраических терминах следующим образом:
Линейный код V является циклическим тогда и только тогда, когда V является идеалом в кольце Fn.
В самом деле, если V - идеал, то для всякого кодового вектора (многочлена) а(х) ∈ V имеем ха(х) ∈ V, т. е. циклический сдвиг снова является кодовым вектором.
Обратно, если V - циклический код, то для всякого кодового вектора а(х) его последовательные циклические сдвиги ха(х), х2а(х), ..., хn-1а(х) также являются кодовыми векторами.
Остается показать, что для всякого многочлена
b(x) = b0 + b1x + b2x2 + ... + bn-1xn-1
произведение b(х)а(х) является кодовым вектором. Мы имеем:
b(х)а(х) = b0a(x) + b1xa(x) + b2x2a(x) + ... + bn-1xn-1a(x). (5)
Согласно сказанному выше, каждое слагаемое в (5) принадлежит кодовому пространству, но тогда и вся сумма обладает этим свойством. Итак, V - идеал.
Не вполне ясно пока, какова польза полученного нами описания циклического кода. Следующее утверждение проливает свет на этот вопрос.
Во всяком идеале V кольца Fn существует фиксированный многочлен g(x), которому кратен всякий многочлен идеала V.
Иными словами, любой многочлен а(х) ∈ V можно представить в виде произведения фиксированного многочлена g(x) ∈ V и некоторого подходящего многочлена s(x) ∈ Fn:
a(x) = g(x)s(x). (6)
Для доказательства рассмотрим ненулевой многочлен g(x) наименьшей степени, принадлежащий идеалу. Если a(x) произвольный многочлен из V, то разделим его на g(x) с остатком:
a(x) = g(x)s(x) + r(x). (7)
Это можно сделать по обычным правилам деления многочлена на многочлен; степень остатка r(х) будет меньше степени делителя g(x). Первое слагаемое в правой части (7) принадлежит V (в силу определения идеала). Поскольку и многочлен а(х) принадлежит V, то остаток r(х), равный разности
a(x) - g(x)s(x)
двух элементов из V, также должен принадлежать идеалу. Если предположить, что r(х) - ненулевой многочлен, то приходим к противоречию: многочлен r(х), принадлежащий идеалу, имеет степень, меньшую степени g(x). Следовательно, r(х) = 0 и выполняется равенство (6).
Многочлен g(x) называется порождающим многочленом идеала V (или соответствующего циклического кода).
Таким образом, если известен порождающий многочлен кода, то тем самым известны и все кодовые многочлены - их список исчерпывается всевозможными произведениями g(x)s(x), где s(x) - произвольный многочлен степени, меньшей n.
Вспомним, что для задания произвольного кода нужно указать полный список кодовых слов, а для задания линейного кода - список базисных кодовых векторов. Для циклического же кода, как мы выяснили, достаточно указать всего лишь один кодовый многочлен, а именно - порождающий многочлен g(x).
По порождающему многочлену легко найти порождающую матрицу циклического кода. Пусть
g(x) = g0 + g1x + ... + gmхm
- многочлен степени m и k = n - m. Рассмотрим следующие многочлены:
g(x), xg(x), x2g(x), ..., xk-1g(x). (8)
Все они являются кодовыми, степень их очевидно не превосходит n-1. Нетрудно убедиться, что рассматриваемые как векторы, они образуют линейно независимую систему, и всякий кодовый вектор является их линейной комбинацией. Следовательно, матрица G, составленная из векторов (8), является порождающей матрицей циклического кода. Порядок ее равен k × n и она имеет следующий вид:

В качестве примера рассмотрим двоичный циклический код длины 7 с порождающим многочленом g(x) = 1 + x2 + x3 = (1011000). Так как
xg(x) = x + x3 + x4 = (0101100),
x2g(x) = x2 + x4 + x5 = (0010110),
x3g(x) = x3 + x5 + x6 =(0001011),
то порождающей будет следующая матрица:

Нетрудно убедиться, что данный циклический код эквивалентен коду Хемминга с проверочной матрицей

Вообще, можно показать, что для всякого кода Хемминга имеется эквивалентный ему циклический код.
Очень важно, что среди циклических кодов имеются такие, которые исправляют любое заданное количество ошибок. Именно, справедлива следующая теорема:
Для любых значений m и t(t < 2m - 1/2) существует двоичный циклический код длины 2m - 1, исправляющий все комбинации из t или меньшего числа ошибок и содержащий не более, чем mt проверочных символов.
Доказательство этой теоремы мы здесь не приводим. Скажем лишь, что построение указанных кодов основано на использовании упоминаемых в приложении полей Галуа GF(q) (см. также дополнение 8 к этому параграфу).
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'