
Задачи и дополнения
1. Для разобранного в данном параграфе примера найти число необнаруживаемых тройных ошибок, Какую часть они составляют от общего числа тройных ошибок?
2. Кодовые слова в примере на стр. 42 содержат 9 информационных символов и 7 проверочных, так что общая длина кодового слова равна 16. Такого числа символов достаточно, чтобы исправлять любые одиночные и обнаруживать любые двойные ошибки. Чтобы достичь того же эффекта для кода с повторением, нужно каждый информационный символ повторить 4 раза, так что общая длина кодового слова будет равна 36. Сравнение явно не в пользу кода с повторением. Справедливости ради надо все же отметить, что код с повторением обладает по сравнению с использованным в примере кодом некоторыми преимуществами в смысле обнаружения ошибок более высокой кратности. Предлагаем читателю найти, например, долю необнаруживаемых тройных ошибок для указанного кода с повторением и сравнить ответ с результатом задачи 1. Интересно найти также долю исправимых (!) тройных ошибок для этого кода.
3. Пример из данного параграфа обобщается следующим образом (смотри также дополнение 12 к § 11). Пусть каждое сообщение кодируется двоичным словом длины mn. Расположим все символы в прямоугольную таблицу (матрицу) с m строками и n столбцами:
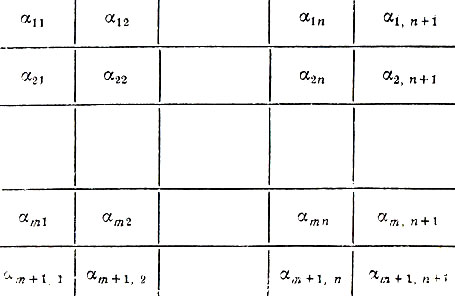
Таблица 17
Как и прежде, добавим к каждой строке и к каждому столбцу по одному проверочному символу, так чтобы во всех строках и столбцах получились четные суммы. Аналогично прежнему выбираем символ αm+1, n+1. Полученное множество слов образует код, исправляющий любые одиночные и обнаруживающий любые двойные ошибки.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'