8. Коды - антиподы

Мы выяснили, что при построении помехоустойчивых кодов не обойтись без дополнительных символов, которые должны быть присоединены к кодовым словам безызбыточного кода. Эти символы уже не несут информации о передаваемых сообщениях, но могут дать информацию о происшедших при передаче ошибках. Иными словами, их назначение - контролировать правильность передачи кодового слова. Вводимые дополнительные символы так и называют контрольными (или проверочными).

Самый незатейливый способ, позволяющий исправлять ошибки, состоит в том, что каждый информационный символ повторяется несколько раз, скажем, символ 0 заменяется блоком из n нулей, а символ 1 - блоком из n единиц. При декодировании n-буквенного блока, содержащего, быть может, ошибочные символы, решение принимается "большинством голосов". Если в принятом блоке нулей больше, чем единиц, то он декодируется как 00 ... 0 (т. е. считается, что был послан нулевой символ), в противном случае - как 11 ... 1. Такое правило декодирования позволяет верно восстановить посланные символы, если помехи в канале искажают менее половины символов в каждом передаваемом блоке. Если длину блока n выбрать достаточно большой, то мы практически обезопасим себя от возможных ошибок, однако передача сообщений будет идти черепашьими темпами. По этой причине указанный код (его называют кодом с повторением) не имеет большого практического значения, однако правило его декодирования ("голосование") содержит в себе весьма полезную идею, которая с успехом применяется в других, практически более интересных помехоустойчивых кодах. Об этом речь пойдет дальше (см. §§ 17, 18), а сейчас постараемся выяснить, на что мы можем рассчитывать при минимальной избыточности, когда к каждому кодовому слову добавляется всего лишь один проверочный символ. Пусть α₁α₂ ... α_n - двоичное кодовое слово. Выберем проверочный символ α_n+1 с таким расчетом, чтобы на его значение одинаково влиял каждый из символов данного слова. Это естественное требование будет выполнено, если, например, положить α_n+1 = α₁ + α₂ + ... + α_n (mod 2). Тогда проверочный символ α_n+1 будет равен нулю, если в кодовом слове α₁α₂ ... α_n содержится четное число единиц, и единице - в противном случае. Например, присоединяя таким образом проверочный символ к слову 1010, получаем слово 10100, а из слова 1110 получим слово 11101.

Нетрудно видеть, что все удлиненные кодовые слова α₁α₂ ... α_nα_n+1 содержат четное число единиц, т. е.

Допустим, что в процессе передачи в удлиненнее кодовое слово α₁α₂ ... α_nα_n+1 вкралась одна ошибка (или даже любое нечетное число ошибок). Тогда в искаженном слове α'₁α'₂ ... α'_nα'_n+1 число единиц станет нечетным. Это и служит указанием на искажение в передаче слова. В конечном итоге все сводится к проверке соотношения (1) для символов принятого слова, что легко сделает простейшее вычислительное, устройство - сумматор по модулю 2. Итак, правило приема следующее: если равенство (1) выполняется, считаем, что сообщение передано правильно, в противном случае отмечаем, что произошла ошибка и, когда это возможно, требуем повторить передачу кодового слова. Понятно, что иначе ошибки не исправить. Например, если принято "неправильное слово" 11100, то одинаково возможно, что было послано любое из кодовых слов:

Каждый из перечисленных случаев соответствует одной ошибке, а ведь ошибки могли произойти даже в трех, а то и в пяти символах.

Еще большая неприятность подстерегает нас в случае двойной ошибки или вообще четного числа ошибок. Ведь тогда соотношение (1) не нарушится, и мы воспримем искаженное слово как верное.

Описанный код, который называют кодом с общей проверкой на четность, позволяет, следовательно, обнаружить любое нечетное число ошибок, но "пропускает" искажения, если число ошибок четно.

Код с повторением и код с общей проверкой на четность - до некоторой степени антиподы. Возможности первого исправлять ошибки теоретически безграничны, но он крайне "медлителен". Второй очень быстр (всего один дополнительный символ), но зачастую "легкомыслен". В реальных каналах связи, как правило, приходится считаться с возможностью ошибок более чем в одном символе, поэтому в чистом виде код с общей проверкой на четность применяется крайне редко. Гораздо чаще применяют коды с несколькими проверочными символами (и, соответственно, с несколькими проверками на четность). Они позволяют не только обнаруживать, но и исправлять ошибки, и не только одиночные, но и кратные, и притом делать это гораздо эффективнее, чем упоминавшийся нами код с повторением. Это можно проиллюстрировать на одном красноречивом и в то же время простом примере.

Рассмотрим множество всех двоичных слов длины 9 (с их помощью можно закодировать 2⁹ = 512 сообщений). Расположим символы каждого слова α₁α₂ ... α₉ в квадратной таблице следующим образом:

Таблица 14

К каждой строке и к каждому столбцу этой таблицы добавим еще по одному (проверочному) символу с таким расчетом, чтобы в строках и столбцах получившейся таблицы (таблица 15) было четное число единиц.

При этом, например, для первой строки и первого столбца будут выполняться проверочные соотношения:

и аналогично для остальных строк и столбцов. Заметим, что

Обе эти суммы равны 0, если в слове α₁α₂ ... α₉ четное число единиц, в противном случае обе они равны 1. Это дает возможность поместить в таблице 15 еще один проверочный символ β₇, равный

Таблица 15

Например, слову 011010001 отвечает следующая таблица:

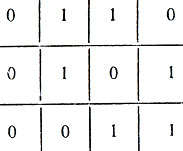
Таблица 16

Эти "маленькие хитрости" позволяют, оказывается, исправить любую одиночную ошибку, возникшую в процессе передачи, а сверх того и обнаружить любую двойную ошибку. В самом деле, если произошла одна ошибка, то нарушаются проверочные соотношения ровно для одной строки и ровно для одного столбца, как раз той строки и того столбца, на пересечении которых стоит ошибочный символ. Если же произошла двойная ошибка, то это приводит к нарушению проверок на четность либо в двух строках, либо в двух столбцах, либо сразу в двух строках и двух столбцах. По этим признакам мы и обнаруживаем двойную ошибку. (Однако исправить ее мы не можем - почему?).

Добавим к сказанному, что данный код позволяет обнаруживать многие, хотя и не все, ошибки более высокой кратности (в трех, четырех и т. д. символах). Например, обнаруживаются тройные ошибки в символах α₁, α₂, α₃ или в символах α₁, α₂, α₆. А вот тройная ошибка в символах α₁, α₂, α₅ не может быть обнаружена, она будет воспринята как одиночная.

Продемонстрированное в этом примере сочетание проверок на четность по строкам и столбцам допускает широкие обобщения. О простейшем из них говорится в дополнении 3.