
2. Шифры, шифры, шифры...
Приемов тайнописи - великое множество, и, скорее всего, это та область, где уже нет нужды придумывать что-нибудь существенно новое. Наиболее простой тип криптограмм - это так называемые подстановочные криптограммы. Составляя их, каждой букве алфавита сопоставляют определенный символ (иногда тоже букву) и при кодировании всякую букву текста заменяют на соответствующий ей символ. В рассказе "Золотой жук" Эдгара По приводится как раз пример подстановочного шифра.
Автор рассказа наглядно демонстрирует, что расшифровка подобных криптограмм не составляет большой проблемы. Все основывается на том (за подробностями отсылаем читателя к оригиналу), что различные буквы естественного языка - английского, русского или какого-либо другого - встречаются в осмысленных текстах неодинаково часто. Следовательно, то же самое верно для соответствующих им знаков. В еще большей мере это относится к буквосочетаниям из двух или нескольких букв: лишь некоторые из них часты, многие же вообще не употребляются.
Анализируя частоту появления тех или иных знаков я их сочетаний (именно так поступает герой Эдгара По), можно с большой уверенностью восстановить буквы зашифрованного текста. Даже если в каких-то частях текста возникает неоднозначность, она легко устраняется по смыслу. Этот метод (он именуется частотным анализом) основывается, таким образом, на заранее известных частотах зашифрованных знаков. В следующей таблице указаны относительные частоты букв русского языка.
Буквы "е" и "ё", а также "ь", "ъ" кодируются обычно одинаково, поэтому в таблице они не различаются. Как явствует из таблицы, наиболее частая буква русского языка - "о". Ее относительная частота, равная 0,090, означает, что на 1000 букв русского текста приходится в среднем 90 букв "о". В таком же смысле понимаются относительные частоты и остальных букв. В таблице 2 не указан еще один "символ" - промежуток между словами. Его относительная частота наибольшая и равна 0,175.
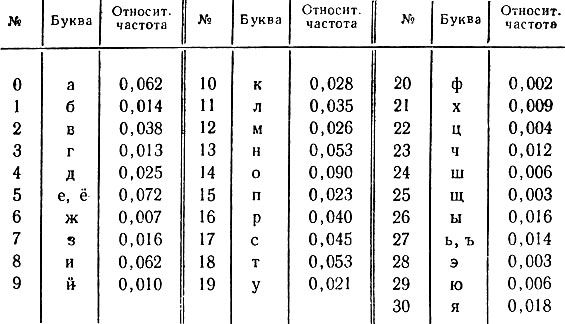
Таблица 2
С помощью таблицы 2 читатель сумеет, по-видимому, расшифровать такую криптограмму (расшифровку и пояснения см. в дополнении 1):
Цярснсмщи ямякзж онкдждм мд снкыйн гкю онгрсямнбнцмщф йпзоснвпялл мн б гптвзф рктцяюф нм ркнемдд.
Ненадежность подстановочных криптограмм (сравнительная легкость их расшифровки) была замечена уже давно, и потому в разное время предлагались различные другие методы шифрования. Среди них важное место занимают перестановочные криптограммы. При их составлении весь текст разбивается на группы, состоящие из одинакового, числа букв, и внутри каждой группы буквы некоторым образом переставляются. Если группа достаточно длинная (иногда это весь текст целиком), то число возможных перестановок очень велико, отсюда большое многообразие перестановочных криптограмм. Мы рассмотрим один тип перестановочной криптограммы, которая составляется при помощи так называемого ключевого слова. Буквы текста, который должен быть передан в зашифрованном виде, первоначально записываются в клетки прямоугольной таблицы, по ее строчкам. Буквы ключевого слова пишутся над столбцами и указывают порядок (нумерацию) этих столбцов способом, объясняемым ниже. Чтобы получить закодированный текст, надо выписывать буквы по столбцам с учетом их нумерации. Пусть текст таков: "В связи с создавшимся положением отодвигаем сроки возвращения домой. Рамзай". Используем для записи текста, в котором 65 букв, прямоугольную таблицу 11 × 6, в качестве ключевого возьмем слово из 6 букв "запись", столбцы занумеруем в соответствии с положением букв ключевого слова в алфавите. В результате получится следующая кодовая таблица:

Таблица 3
Выписывая буквы из столбцов таблицы 3 (сначала из первого, затем из второго и т. д.), получаем такую шифровку:
Ссшоидмвщомвсвпноеиадаязмомирзноавоилевсоемзздсжоговийииаяетакряр
Ключевое слово известно, конечно, и адресату, который поэтому без труда расшифрует это сообщение. Но для тех, кто этим ключом не владеет, восстановление исходного текста весьма проблематично (хотя в принципе и возможно). Частотный анализ здесь по вполне понятным причинам не решает задачи. В лучшем случае, поскольку частоты букв примерно такие, как в таблице 2, он позволяет предположить, что было применено перестановочное кодирование.
Использование ключевого слова, конечно, не обязательно, можно было указать нумерацию столбцов цифровым ключом, в данном случае числом 214356. Слово удобнее, если ключ надо хранить в памяти (что немаловажно для конспирации).
Имеется ряд шифров, в которых совмещены приемы подстановочного и перестановочного кодирования, шифр можно еще более усложнить, если дополнительно к этому каждую букву заменять не одним, а двумя или несколькими символами (буквами или числами). Вот пример. Расположим буквы русского алфавита в квадратной таблице 6×6 произвольным образом, например так, как в следующей таблице.

Таблица 4
Каждую букву шифруем парой цифр: первая цифра это номер строки, в которой стоит данная буква, вторая - номер столбца. Например, букве "б" соответствует обозначение 21, а слову "шифр" - обозначение 51022304.
Еще большие трудности для криптоанализа представляет шифр, связываемый с именем Тритемцуса. Этот шифр является развитием рассматриваемого в дополнении 2 кода Цезаря и состоит в следующем. Буквы алфавита нумеруются по порядку числами 0, 1, ..., 30 (см. табл. 2). При шифровании ключевое слово (или номера его букв) подписывается под сообщением с повторениями, как показано ниже:
всвязиссоздавшимсяположениемотодвигаемсрокивозвра записьзаписьзаписьзаписьзаписьзаписьзаписьзаписьз щениядомойрамзай аписьзаписьзапис
Каждая буква сообщения "сдвигается" вдоль алфавита по следующему правилу: буква с номером m, под которой стоит буква ключевого слова с номером k, заменяется на букву с номером l = m + k (если m + k < 31) или букву с номером l = m + k - 31 (если m + k ≥ 31). Например, первая буква "в" сдвигается на 7 букв и заменяется буквой "й", следующая буква "с" остается без изменения и т. д. Таким образом, номер l кодирующей буквы вычисляется по формуле:
l = m + k (mod 31). (1)
В цифровых обозначениях исходное сообщение и повторяемое ключевое слово запишутся в следующем виде:
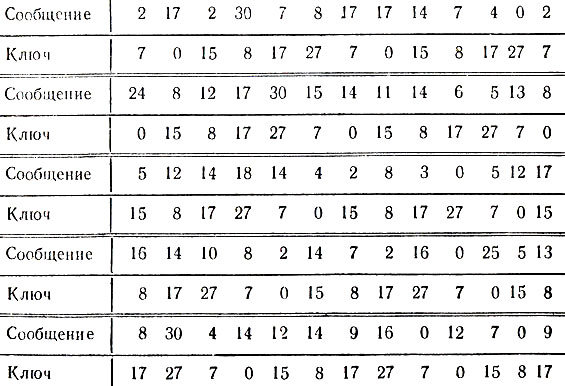
Таблица 5
После суммирования верхней и нижней строки по модулю 31 получаем последовательность чисел:
9.17.17.7.24.4.24.17.29.15.21.27.9.24.23.20.3.26.22.14.26. 22.23.1.20.8.20.20.0.14.21.4.17.16.20.27.12.12.1.24.0.6. 15.2.29.15.19.12.7.25.20.21.25.26.11.14.27.22.26.12.7. 12.22.8.26.
Наконец, заменяя числа на буквы, приходим к закодированному тексту:
йссзшдшсюпхьйшчфгыцоыцчбфиффаохдсрфьммбшажпвюпумзщфхщылоьцымзмциы
Если ключевое слово известно, то дешифровка производится безо всякого труда на основе равенства:
m = l - k (mod 31).
Чрезвычайно трудно расшифровать подобный текст, если ключ неизвестен, хотя в истории криптографии были случаи, когда такие тексты разгадывались. Дело в том, что повторяемость ключевого слова накладывает некоторый отпечаток на криптограмму, а это может быть обнаружено статистическими методами, которые позволяют судить о длине ключевого слова, после чего расшифровка значительно упрощается.
Мы рассмотрели лишь некоторые способы составления криптограмм. Заметим, что комбинируя их, можно получать шифры, еще более труднодоступные для расшифровки. Однако вместе с этим возрастают трудности пользования шифром для отправителя секретного сообщения и адресата, поскольку сильно усложняется техника шифровки и дешифровки даже при наличии ключа.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'