Задачи и дополнения

1. Часто по разным соображениям для кодирования сообщений используют не все последовательности в данном алфавите, а только некоторые из них, удовлетворяющие тем или иным ограничениям. Будем рассматривать, например, n-буквенные двоичные слова с фиксированным числом t единиц (или, как говорят, слова постоянного веса t). Сколько всего таких слов - нетрудно подсчитать. Каждое из них получится, если мы выберем некоторым образом t позиций из n, и запишем в них единицы, а в остальных n-t позициях - нули. Значит, число всех слов постоянного веса совпадает с числом сочетаний из n элементов по t, т. е. равно

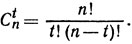
2. Сложнее найти число всех двоичных слов длины n, не содержащих несколько нулей подряд. Обозначим это число через s_n. Очевидно, s₁ = 2, а слова длины 2, удовлетворяющие нашему ограничению, таковы: 10, 01, 11, т. е. s₂ = 3. Пусть α₁α₂ ... α_n-1α₁ - такое слово из n символов. Если символ α_n = 1, то α₁ α₂ ... α_n-1 может быть произвольным (n-1)-буквенным словом, не содержащим нескольких нулей подряд. Значит, число слов длины n с единицей на конце равно s_n-1.

Если же символ α_n = 0, то обязательно α_n-1 = 1, а первые n-2 символа α₁ α₂ ... α_n-2 могут быть произвольными с учетом рассматриваемого ограничения. Следовательно, имеется s_n-2 слов длины n с нулем на конце. Таким образом, общее число интересующих нас слов равно

Из полученного соотношения (подобные соотношения называют рекуррентными) легко можно найти числа s_n для любого n. Поскольку s₁ и s₂ известны, то s₃ = s₁ + s₂ = 5; s₄ = s₂ + s₃ = 8, s₅ = s₃ + s₄ = 13 и т. д. Полученная последовательность чисел

в которой каждый последующий член равен сумме двух предыдущих, - это хорошо известный в математике ряд Фибоначчи. О многих интересных свойствах чисел Фибоначчи и их разнообразных приложениях можно прочесть в популярной брошюре [21], а также в недавно изданной книге [6]. В частности, можно убедиться (см. [21]), что n-ый член ряда Фибоначчи вычисляется по формуле:

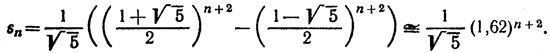
3. Соединим оба предыдущих ограничения и найдем число двоичных слов постоянного веса t, не содержащих нескольких нулей подряд.

Рассуждать можно так. Пусть q = n-t - число нулей в рассматриваемых словах. В любом слове имеется q-1 промежутков между ближайшими нулями, в каждом из которых находится одна или несколько единиц (см. рис. 1). Предполагается, конечно, что q ≤ n/2. В противном случае (при q > n/2) нет ни одного слова без рядом стоящих нулей.

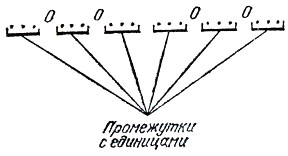
Рис. 1

Если из каждого промежутка удалить ровно по одной единице, то получим слово длины n-q+1, содержащее q нулей. Легко видеть, что любое такое слов о может быть получено указанным образом из некоторого (и притом только одного) n-буквенного слова, содержащего q нулей, никакие два из которых не стоят рядом. Значит, искомое число совпадает с числом всех слов длины n-q+1, содержащих ровно q нулей, т. е. равно (см. дополнение 1).

4. Используя результаты дополнений 2, 3, убедиться в справедливости тождества:

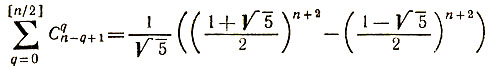
(символ [n/2] означает наибольшее целое число, не превосходящее n/2).

5. При каком q число двоичных слов из дополнения 3 максимально?

6. Показать, что число всех n-буквенных d-ичных слов, в которых один из символов встречается фиксированное число t раз, равно C^t_n(d - 1)^n-t (ср. дополнение 1).

7. Обобщить результаты дополнений 2 и 3 применительно к d-ичному алфавиту.