Задачи о пентамино

"Доски", представленные на рисунках к задачам от 1 до 32, требуется заполнить наборами пентамино, состоящими из всех 12 элементов. Если укладка должна быть выполнена каким-то особым способом (например, конструкция должна состоять из двух одинаковых частей), то это показывается на рисунках жирной линией, разделяющей "доску" на указанные части.

1. Сложите из 12 пентамино прямоугольник размером 3×20.

2. Используя все пентамино, сложите прямоугольник размером 4×15.

3. Сложите из всех пентамино прямоугольник размером 5×12.

4. Заполните пентамино прямоугольник размером 6×10.

5.

6.

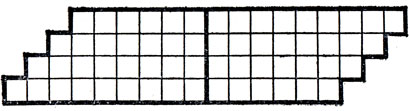
7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

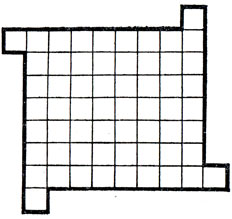
18.

19.

20. Каждый из этих прямоугольников должен содержать одно непокрытое поле.

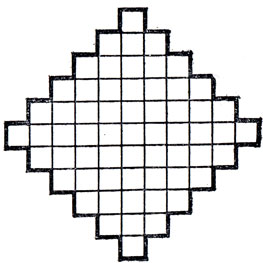
21. Эта "квадратная" доска должна быть заполнена так, что останется одно поле (как показано в гл. VI, это поле не может располагаться в центре квадрата).

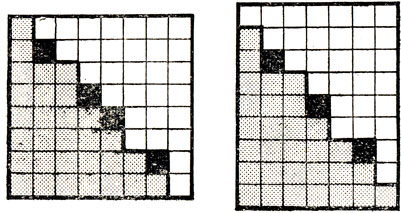
22. Если составить показанный на рисунке слева квадрат размером 8×8 из двух конгруэнтных частей, то одну из них (например, затененную) можно передвилуть как единое целое вдоль другой, образуя укладку показанного справа прямоугольника размером 9×7.

23. Один читатель журнала Fairy Chess Review поставил и решил следующую необычную задачу. С помощью всех 12 пентамино он построил фигуцу неправильной формы, показанную на рисунке. Штриховые линии показывают, как из этой фигуры можно вырезать развертку куба.

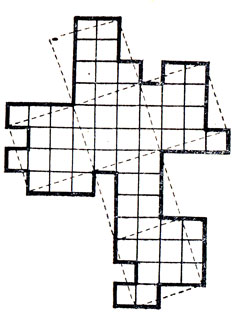
24.

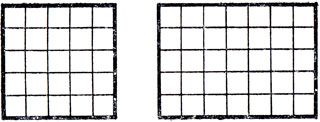
Поскольку существует 2339 укладок прямоугольной доски размером 6×10, то для того, чтобы сделать относящиеся сюда задачи более интересными и увлекательными, следует наложить какие-либо дополнительные требования к подобным укладкам. (Некоторые из таких задач представлены ниже под номерами 25-32.)

25. Постройте два прямоугольника размером 5×6.

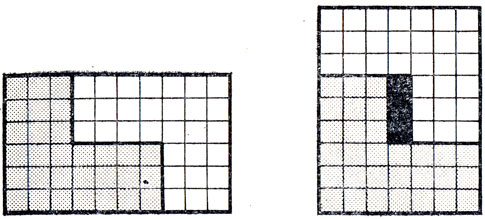
26. Пусть исходный прямоугольник размером 6×10 содержит прямоугольную часть размером 3×5, расположенную внутри прямоугольника.

27. То же требование, но прямоугольная часть должна иметь размер 4×5.

28. Прямоугольник размером 6×10 должен состоять из двух частей, показанных слева. Незатененную часть впоследствии можно сдвинуть как единое целое, образовав показанный справа прямоугольник размером 7×9.

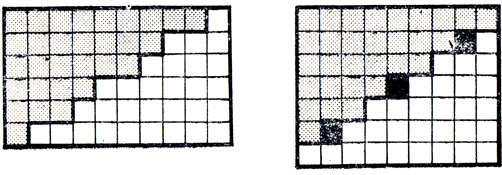
29. Тем же путем, что и в предыдущей задаче, сдвинув затененную часть укладки, получим прямоугольник размером 7×9.

30. Постройте прямоугольник размером 6×10 так, чтобы каждое из 12 пентамино касалось его сторон.

31. Постройте прямоугольник размером 6×10 так, чтобы I-пентамино не касалось его сторон.

32. Случайным образом расположите пентамино на столе, а затем уложите из них прямоугольник размером 6×10, не переворачивая ни одного пентамино (это можно сделать во всех 32 случаях).

33. Задача о 10 квадратах, а) Используя два пентамино, сложите произвольную фигуру из 10 квадратов и найдите два других пентамино, из которых можно сложить такую же фигуру, б) Из четырех оставшихся пентамино сложите фигуру, подобную исходной, в) Из последних четырех пентамино сложите фигуру, подобную предыдущим.

34. Задача о 20 квадратах, а) Из четырех пентамино сложите произвольную фигуру, состоящую из 20 квадратов, б) Из четырех других сложите такую же фигуру, в) Наконец, из последних четырех снова сложите эту фигуру.

35. Задача удвоения, а) Из двух пентамино сложите фигуру, содержащую 10 квадратов, б) Используя два других пентамино, сложите такую же фигуру, в) Наконец, из всех оставшихся пентамино сложите фигуру, подобную исходным, линейные размеры которой должны быть вдвое большими.

Рисунок, приводимый выше, даст вам представление о формах, которые могут быть получены таким способом.

36. На рис. 19 в гл. I было показано, как выпилить все 12 пентамино из куска фанеры размером 6×13, делая по возможности меньше прямых надпилов. Недавно одна читательница из Лондона нашла решение аналогичной задачи для прямоугольников из фанеры размерами 4×19 и 5×15. Мы приглашаем читателя продолжить ее работу и найти разрезы для прямоугольника размером 5×15. (Как и в гл. I, случай U-пентамино требует особого подхода. Видимо, проще вырезать сначала прямоугольник размером 2×3, а уже из него U-пентамино.)

37. Задача утроения. Для каждого из 12 пентамино, используя девять остальных, постройте фигуру, подобную исходному пентамино, но втрое более высокую и втрое более широкую.

38. Четным числом Р-пентамино можно покрыть прямоугольник, имеющий четную площадь. Найдите наименьший прямоугольник, который можно покрыть нечетным числом Р-пентамино.

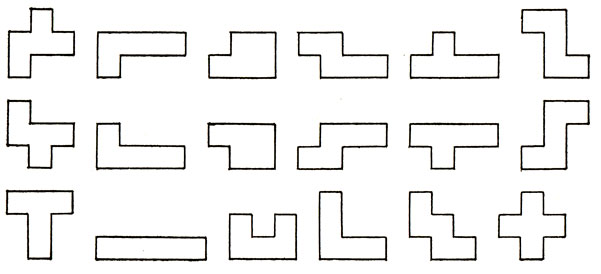
39. Сложите прямоугольник размером 9×10 из 18 односторонних пентамино, показанных ниже. (Напомним, что односторонние пентамино нельзя переворачивать.)