V. Серьезные игры

Симметрия, как бы широко или 
узко мы ни понимали это слово, 
есть идея, с помощью которой 
человек веками пытался 
объяснить и создать порядок, 
красоту и совершенство.

Герман Вейль

Серьезные игры

"Математик, так же как художник или поэт, создает узоры, и если его узоры более устойчивы, то лишь потому, что они составлены из идей". В книге "Апология математики", изданной в Кембридже, эти слова не относятся, конечно, к такой малой частности, как геометрические мозаики. Но, право же, и в этих узорах есть своя идея, не лишенная ни красоты, ни глубины. В сущности, мы живем среди мозаик. Кирпичная кладка домов, паркет в них, стены в ванной комнате - все это они: одни и те же фигуры раз за разом повторяют сами себя - одна к одной, сплошняком. Гравюры Эсхера "Всадники", "Лебеди", "Восемь голов", "Мозаика. II", а также многие другие из его работ тоже представляют собой плоскость, полностью, без "зазоров" покрытую фигурами, которые в то же время не налезают друг на друга. Это и есть то, что геометр назовет мозаикой. А с точки зрения портного или обувщика, математическая мозаика - это выкройка без потерь. Впрочем, мозаичный узор - еще и искусство. Оно достигло наивысшего расцвета семь веков назад в Испании. Правда, мавры не могли заполнять свои плоскости изображениями зверей или птиц, а тем более человека - Коран в ином, правда, смысле, чем Библия, но тоже запрещает "сотворять себе кумира", и потому дивная стенная роспись Альгамбры, дворца арабских султанов в Гренаде,- это мозаика из абстрактных фигур. Но это как раз то, что нас сейчас интересует!

Серьезные игры

"Математики - вроде французов: когда говоришь с ними, они переводят твои слова на свой язык и сразу получается что-то совсем другое" - в шутке Гёте много смысла. Да, математик вкладывает свою идею в прекрасное искусство мавров. Его даже радует, что в Коране есть запрещение изображать живых тварей. Ближе всего его сердцу узоры, составленные из одинаковых правильных многоугольников,- правильные математические мозаики.

А какие они могут быть? Первое, что приходит в голову,- правильная четырехугольная квадратная мозаика, порождение ограниченности нашей нынешней строительной эстетики, преследующая нас дома и на улице. Какие еще мозаики могут встретиться нам в этом мире? "Треугольная",- скажете вы, и будете правы: равносторонний треугольник заполнит собою всю плоскость. Двуугольных фигур не бывает, и потому следующий претендент на роль мозаичного кирпича...?

"Правильный пятиугольник!"- возможно, скажете вы, и ошибетесь!

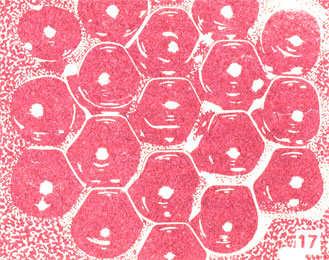
Правильные пятиугольники не смогут встретиться в одной вершине, втроем они не сомкнутся вокруг нее, а вчетвером налезут друг на друга. Следующий испытуемый - правильный шестиугольник Тут все в порядке: угол между любыми двумя сторонами равен 120 градусам, значит, три их как раз и образуют 360. Такая мозаика - она называется гексагональной - часто встречается в природе. Это пчелиные соты (16) или, например, поверхность жидкости, подвергнутой высокочастотной вибрации,- такую мозаику можно "остановить" с помощью стробоскопа (17).

Но шестиугольная мозаика - последняя наша удача.

Право, на праведную геометрическую жизнь имеют мозаики только трех типов: {4,4}, {3,6} и {6,3}. Это опять символы Шлефли, и они по-прежнему означают, что в вершине мозаики могут сойтись либо четыре четырехугольника, либо шесть треугольников, либо, наконец, три шестиугольника - и никаких иных правильных многоугольников. Все эти мозаики, переходящие благодаря воображению художника одна в другую, вы увидите на гравюре Эсхера "Метаморфозы. II".

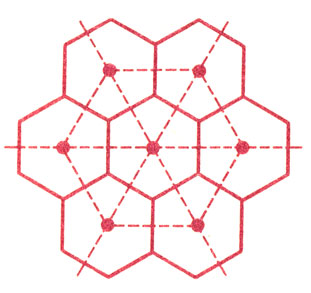
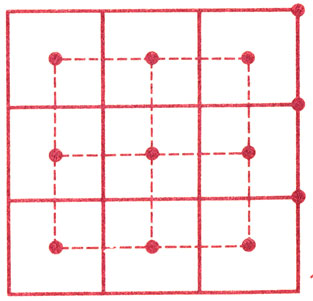
Две последние мозаики очень похожи друг на друга, хотя внешне у них все вроде бы наоборот: вершины одной служат центрами граней другой (18, 19). Символы их {3,6} и {6,3} совсем не случайно симметричны, и не случайно треугольная и гексагональная мозаики называются двойственными. Про квадратную же мозаику {4,4} приходится сказать, что она двойственна сама себе.

"Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математики",- пишет в своей прекрасной книге "Симметрия" Герман Вейль. Его высказывание ни в явном, ни в неявном виде не содержит гиперболы: среди декоративных узоров древности, главным образом в египетских орнаментах, дошедших до нас, содержатся все возможные виды симметричного расположения на плоскости любых фигур, а таких видов, оказывается, всего семнадцать. "Вряд ли возможно переоценить глубину геометрического воображения и изобретательность, запечатленные в этих узорах,- продолжает Вейль.- Их построение далеко не тривиально в математическом отношении... 17 видов симметрии, в неявном виде известных еще египетским ремесленникам, исчерпывают все возможные случаи. Довольно странно, что доказательство этого факта было дано лишь в 1924 г. Д. Пойя".

Еще более, пожалуй, странно, что такой крупный специалист, как Герман Вейль, тут ошибается: все эти семнадцать расположений были найдены известным русским ученым Евграфом Степановичем Федоровым и описаны в его работе "Симметрия на плоскости", изданной в Санкт-Петербурге в 1891 году. Впрочем, проблема эта интересовала многих ученых. Шестнадцать из семнадцати групп указал француз Камилл Жордан в "Мемуаре о группах движения" в 1869 году, тринадцать - немец Леонгард Зонке спустя еще пять лет. И, надо сказать, было из-за чего тратить время и бумагу. Речь шла не просто о математических курьезах - создавался подход к пониманию строения кристаллов, "каменных цветов", удивительных созданий Природы.

Серьезные игры (16)

Первое разумное суждение о том, в чем загадка правильной формы кристаллов, было высказано, видимо, Иоганном Кеплером в трактате "О шестиугольном снеге". Оно относится к снежинкам. Почему они всегда шести-лучевые или шестиугольные? - спрашивал он себя. И пришел к гениальному для тех времен выводу: потому, что невидимые капельки водяного пара шарообразны и на холоде приклеиваются друг к другу таким образом, что каждая сцепляется с двенадцатью другими, "подобно зернам граната". Это было в начале XVII века и никто еще не сумел заглянуть внутрь вещества, и даже Ньютон еще не затеял своего спора с Грегори о целующихся сферах.

"Чтобы познать невидимое, смотри внимательно на видимое" - сказано в одной древней книге. сознательно или подсознательно этому принципу следовали все ученые, которым предстояло заложить фундамент новой науки - кристаллографии. Французский минералог Рене Жюст Гаюи однажды случайно уронил кристалл известкового шпата. Подобрав кусочки, он увидел, что они в точности повторяют форму разбившегося кристалла. Заинтригованный, он стал один за другим разбивать кристаллы из своей огромной коллекции и, как писал впоследствии его биограф, "продолжая трудиться на этом поприще, сделался основателем кристаллографии".

Вместе с тем, правда, Гаюи получил и насмешливое прозвище "кристаллокласт" - "разрушитель кристаллов", которое присвоили ему коллеги, предпочитавшие умозрительный подход к проблеме кристаллов слишком уж, на их взгляд, грубому натурному эксперименту. Но прошли долгие десятилетия, прежде чем почти одновременно Е. С. Федоров в России и А. Шенфлис в Германии, независимо друг от друга - один шел геометрическим путем, а другой воспользовался алгебраическим аппаратом теории групп - вывели все возможные в пространстве группы симметрии, которые определяют собой и все разнообразие кристаллических форм в природе. Любопытно, что когда они сверили результаты своих работ, то оказалось, что Федоров насчитал 229 возможных способов сочетания частиц в кристалл, а Шенфлис - 227. Федоров пропустил один способ, замеченный Шенфлисом, но тот зато проглядел целых три, указанных Федоровым. Немедленный обмен письмами позволил исправить недосмотры, и с тех пор в кристаллографии твердо установлено, что федоровских групп ровно 230.

Серьезные игры (17)

"Все мои работы - это игры, серьезные игры",- говорил о себе голландский художник Мауриц Корнелис Эсхер, гравюрами которого иллюстрирована не только эта, но и множество других книг, вышедших в разных странах и так или иначе связанных с наукой. Исследования Федорова и Шенфлиса тоже довольно долго рассматривались как некие математические забавы и развлечения, не имеющие отношения к правде жизни. Еще Рентген не открыл своих знаменитых лучей, Беккерель - радиоактивности, Томсон - электрона и, наконец, Лауэ не обнаружил рассеяния рентгеновских лучей кристаллами. Все эти события должны были произойти для того, чтобы федоровские группы легли в основу точного и математически строгого расчета архитектуры кристаллов.

"Федоровская группа - это лишь канва, по которой природа может вышивать бесконечно разнообразные узоры атомных расположений. Но типов канвы всего 230, и великая заслуга Федорова и Шенфлиса заключается в том, что они установили этот факт и перечислили все возможные случаи. Чтобы в полной мере оценить удивительную проницательность, которую проявили эти ученые при выводе пространственных групп, нужно иметь в виду, что в те времена действительное расположение атомов в кристаллах совершенно не было известно". Цитата взята из книги П. М. Зоркого "Архитектура кристаллов". В ней автор позволил себе любопытное признание: "По-видимому, в последнее время несколько изменились функции научно-популярной литературы. Стремительное увеличение объема научных знаний часто не позволяет ученым и инженерам следить за развитием смежных областей науки, пользуясь специальными статьями и монографиями. Слишком много времени и сил требует основная работа. На помощь приходит научно-популярная литература. Она дает возможность сохранять широту кругозора, а иногда (автор знает об этом по собственному опыту) может пригодиться в основной работе".

Слова эти, написанные в наше время, в конце шестидесятых годов, едва ли вызвали бы возражение и в прежние времена. Евграф Степанович Федоров начал работать над своей первой монографией "Начала учения о фигурах" шестнадцатилетним гимназистом. И еще шестнадцать лет прошло, прежде чем он ее кончил. Причиной тому, видимо, не одна лишь необычная фундаментальность мышления, которая замечалась у будущего академика Петербургской академии наук. Виной тому и популярная литература, которая сбила его с прямого математического пути, заставила заинтересоваться кристаллографией, поступить в Горный институт, закончить его и потерять возможность разграничивать математику и кристаллографию на "основную" и "смежную" науки.

Нечто похожее случилось и с Маурицем Корнелисом Эсхером.

"В наше время, когда искусство и наука живут в различных областях духовной жизни и при этом стремятся разойтись все дальше и дальше друг от друга, столь удивительно вдруг встретить художника, который в своей творческой деятельности занят проблемами, лежащими в основании целых наук и нескольких математических дисциплин. подобное не случалось с тех времен, когда художники открывали законы перспективы и были пионерами в анатомических исследованиях",- пишет во введении к своей книге "Проблемы симметрии в периодических рисунках М. К. Эсхера" профессор Амстердамского университета Каролина Генриетта Мак-Гиллаври. Книга эта, состоящая из более чем сорока работ художника и соответствующего кристаллографического толкования их, служит учебным пособием для студентов.

"Я часто удивлялся своей мании создавать периодические рисунки,- писал сам художник.- Однажды я спросил своего друга, психолога, в чем причина моей увлеченности ими, но его ответ, что меня ведет здесь примитивный инстинкт повторения сделанного, ничего не объяснил".

Серьезные игры (18)

И в самом деле, каким инстинктом объяснить поразительную по плавности перехода от рыбы, плывущей в темных глубинах моря, к птице, летящей в прозрачной высоте, гравюру "Небо и вода. I" или четкую в своем стремлении связать живое с неживым гравюру "Рептилии"? А ведь обе они построены на "повторении сделанного".

"Почему я одинок в этом деле?- продолжает Эсхер.- Отчего никто из моих коллег-художников не интересуется фигурами, которые входят одна в другую? А ведь фигуры эти подчиняются неким вполне объективным законам, которые всякий художник мог бы использовать в своей работе!

Свой первый рисунок такого рода я сделал в 1922 году. Он представлял собой соединение восьми различных человеческих голов^*. В последующие годы я нарисовал около полутораста картинок такого типа. Я не мог удержаться от удовольствия повторять на бумаге одни и те же формы без зазоров между ними. Рисунки эти поглощали у меня вначале массу времени, потому что я ничего не слышал о кристаллографии и не знал даже, что мои игры основаны на правилах, хорошо изученных учеными.

^* (Гравюра "Восемь голов". См. "Указатель гравюр Маурица Корнелиса Эсхера, иллюстрирующих книгу".)

Много лет спустя я впервые познакомился с кристаллографическими теориями... таким путем установился плодотворный контакт между математиками и мною".

Мозаики Альгамбры пленили воображение молодого художника, путешествовавшего по Испании. Но лишь знакомство с математической стороной кристаллографии, с федоровскими группами в частности, помогло ему осознать истоки собственной увлеченности. И то, что ему и окружающим казалось игрой ума, стало вдруг учебным пособием, более того - предметом изучения и причиной вдохновения математиков. Гравюра "День и ночь" - лишь один из примеров тому. Удивительное дело! Эсхер создал ее в 1938 году, когда еще и в помине не было идеи антисимметрии (хотя высказана она была Хеешем в 1929 году, но в науку вошла лишь после работ академика А. В. Шубникова, появившихся в конце сороковых годов), однако до сих пор нет и не мыслится лучшей иллюстрации этой важной и глубокой идеи современной науки.

"В 1951 году и в последующие годы А. В. Шубников, Н. В. Белов и другие расширили теорию кристаллографических групп, соединив периодическое повторение форм с периодическим повторением цветов. Эта теория полихроматической симметрии добавляет к 17 федоровским группам 46 двухцветных, 6 трехцветных, 6 четырехцветных и 3 шестицветных. Почти наверное русские не знали, что Эсхер, опираясь на одну лишь свою художническую интуицию, безо всякой математики, предвосхитил многие из полученных ими результатов. Например, очарование его знаменитых мотивов со всадниками увеличивается благодаря тому, что фигуры на них либо белые, либо серые - в зависимости от того, скачут ли они слева направо или справа налево"^*,- пишет неоднократно упоминавшийся в этой книге профессор Гарольд Скотт Макдональд Коксетер.

^* (Мотив со всадниками - гравюру, так и названную "Всадники", вы найдете в этой книге, пользуясь все тем же "Указателем", помещенным в конце ее.)

Серьезные игры (19)

"Что такое красота?- спрашивал профессор Александр Александрович Любищев в своей посмертной статье, в которой он, биолог, размышлял о морозных узорах на окнах.- Одно из самых загадочных явлений природы. И как в законах строения и развития природных тел мы имеем разные уровни, так есть они и в прекрасном. И на самом высшем уровне, может быть, находятся абстрактнейшие математические теории и высшие музыкальные творения гениальных композиторов. Не всем дано подняться на эти вершины, но, как в капле воды отражается солнце, так некоторый намек на высшую красоту мы можем постичь, внимательно рассматривая такое скромное явление, как ледяные узоры на стеклах..."

"Видимо, мыслима какая-то новая кристаллография, которую с полным правом, по образцу неевклидовой геометрии, можно назвать "нефедоровской" - такова основная мысль статьи Любищева. "Я думаю, что физики обращали так мало внимания на ледяные узоры не потому, что считали это пустяками (для истинного ученого нет пустяков в природе),- пишет он,- а потому, что еще не наступил момент для нарождения нефедоровской кристаллографии".

Такой момент, видимо, все-таки уже наступил. В классическом труде академика Алексея Васильевича Шубникова "Симметрия и антисимметрия конечных фигур" к геометрическим операциям симметрии - переносу, повороту, зеркальному отражению - присоединена еще и операция "изменение цвета". Понятие черно-белой симметрии, или антисимметрии, столь удачно иллюстрируемое гравюрой Эсхера "День и ночь", оказалось необычайно плодотворным в таких, например, областях, как изучение расположения диполей в магнитных полях. Академик Николай Васильевич Белов со своими сотрудницами Н. Н. Нероновой и Т. С. Смирновой доказал, что существует ровно 1191 двухцветная федоровская группа.

Теория цветной симметрии развивалась и дальше. Одно из условий, выводимых из нее, гласит, что если пренебречь цветами и все темные тона объединить в один черный, а все светлые - в один белый цвет, то мы сразу получим все известные 46 черно-белых, то есть двухцветных, мозаик.

...Пожалуй, разговор о мозаиках, с которого началась эта глава, увел нас слишком далеко. Впрочем, предощущения грядущих открытий в самых фундаментальных областях знания не так уж необычны для науки. Задолго до первых кристаллографических откровений не кто иной, как Исаак Ньютон, писал: "Нельзя ли предположить, что при образовании кристалла частицы не только становились в строй и в ряды, застывая в правильных фигурах, но также посредством некоторой полярной способности повернули свои одинаковые стороны в одинаковом направлении?" Не правда ли, удивительное провидение? Быть может, спустя всего несколько лет мы с таким же чувством будем перечитывать фразу из статьи Любищева: "Развитие биологии убедило ученых, что есть в природе законы, ограничивающие многообразие форм и регулирующие развитие..."

Серьезные игры

Кристаллографические элементы 
организованности, характерные 
для белков, обещают нам 
наиболее глубоко проникнуть 
в тайны управляемых белками 
жизненных процессов.

Николай Васильевич Белов