IV. Великолепная пятерка

В огромном саду геометрии 
каждый может подобрать 
себе букет по вкусу... 
И ныне наглядное понимание 
играет первенствующую 
роль в геометрии.

Давид Гильберт

Великолепная пятерка

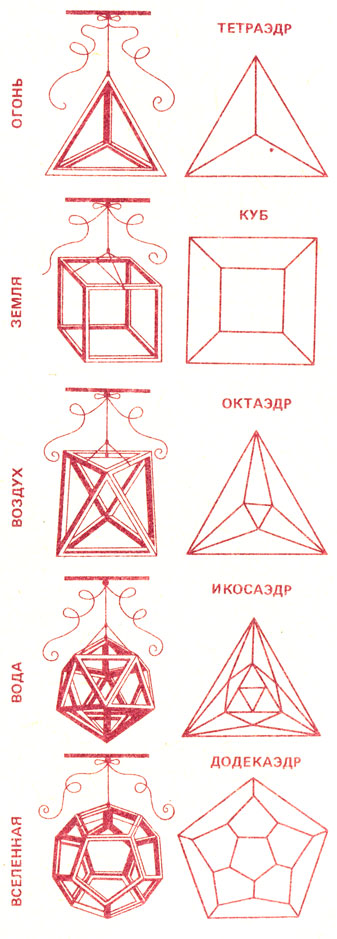
"Греки - это не способные школьники или хорошие студенты, но скорее "коллеги из другого колледжа",- писал профессор Джон Инденсор Литлвуд, один из крупнейших современных английских математиков. Поверим ему и не станем с насмешливым превосходством судить Платона за то, что он считал, будто атомы четырех элементов, из которых строится мир (огня, земли, воздуха и воды), имеют форму правильных выпуклых многогранников - тетраэдра, куба, октаэдра и икосаэдра, а весь мир в целом построен в форме додекаэдра. (На 73-й странице книги пять Платоновых тел сопоставлены с гравюрами Эсхера "Фейерверк", "Итальянский пейзаж. 1923", "Россано, Калабрия", "Второй день творения" и "Другой мир. 1947".) Воздержимся от саркастической улыбки и читая о "пятой сущности", или, по-латыни, "квинтэссенции" алхимиков, хотя их "колледж" чужд нам по духу. Подумаем лучше, почему именно додекаэдр, как показали раскопки в Монте Лоффа под Падуей, был любимой игрушкой этрусских детей 2500 лет назад? И почему он же до наших дней остается излюбленной побрякушкой для взрослых, которые делают из него календарь - по месяцу на каждый из двенадцати его граней (одно из изделий такого рода - брелок для ключей, изготовленный нашим "Автоэкспортом")?

Великолепная пятерка

Куб (или гексаэдр) и правильная пирамида (или тетраэдр) тоже верно служили большим и малым людям - и их созидательной тяге к строительству, и их разрушительной страсти азарта. Свидетельство тому - детские кубики и пирамидки, а также вся архитектура конструктивизма. Но почему же не куб и не пирамида, а совсем другой правильный многогранник - икосаэдр - хранится в Египетском зале Британского музея, и удивленный посетитель может узнать, что это - игральная кость династии Птолемеев? И почему октаэдр - "пространственный ромб" - от древних времен до наших дней неизменно служит светильником, хотя "начинка" его прошла путь от скоротечной плошки до почти вечной йодной лампы?

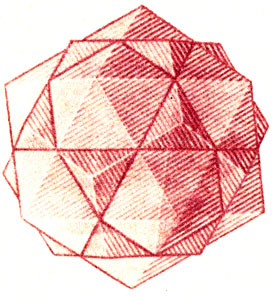
И наконец, главный вопрос: почему Платоновых тел (это математический термин) именно пять? Постарайтесь придумать шестое: выпуклый многогранник, каждая грань которого - один и тот же правильный многоугольник, то есть фигура с равными сторонами и равными углами между ними. Когда попытки ваши кончатся безрезультатно, попробуйте найти способ доказать себе и другим известное любому математику утверждение Евклида: существует только пять правильных выпуклых многогранников. И вне зависимости от успеха этого предприятия вы, вероятно, с большим пониманием, чем прежде, отнесетесь к словам профессора Литлвуда. И вне сомнения, с большим, чем в первый раз, интересом станете рассматривать гравюру Эсхера "Звезды", на которой среди прочих тел легко найти всю нашу "великолепную пятерку".

"Различные ветви геометрии находятся в тесных и часто неожиданных взаимоотношениях друг с другом" - такими словами Давид Гильберт предваряет одну из своих книг. Любой, в том числе и этот, рассказ о геометрии служит подтверждением их правдивости.

Леонардо да Винчи любил изготовлять из дерева каркасные модели многогранников. Когда его друг фра Лука Пачоли издал в 1509 году в Венеции книгу "О божественной пропорции", иллюстрациями к ней послужили пятьдесят девять рисунков, сделанных Леонардо со своих моделей. (Впрочем, Пачоли не остался в долгу: он подсчитал для великого скульптора количество металла, потребного для изготовления статуи всадника,- задача по тем временам нешуточная.)

Великолепная пятерка

Что же божественного нашел в простых геометрических фигурах Лука Пачоли - человек, живший спустя два тысячелетия после Платона? Или это отзвук, прошедший через века и народы, приписываемой ему Плутархом крылатой фразы: "Бог всегда действует геометрически"?

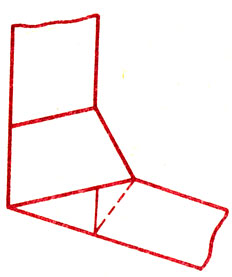
Нет, фра Лука - монах Пачоли - мыслил реалистичнее: бог - геометр не всегда, но в некоторых случаях. А именно когда речь идет о "золотом сечении" - о таком делении отрезка на две неравные части, чтобы отношение большей части к меньшей равнялось отношению всего отрезка к большей его части. Завяжите простым узлом узкую полоску бумаги и осторожно распрямите его (12). Вы получите правильный пятиугольник, а его диагонали как раз и делят друг друга "в среднем и крайнем отношении" - так еще по-другому называют "золотое сечение". Пачоли нашел, что есть тринадцать "эффектов" этой "божественной" пропорции - "ради нашего спасения", как утверждал он. Он искал эти "божественные эффекты" в самых совершенных созданиях математики - пяти Платоновых телах, строил их из стеклянных плиток, а затем раздавал "для коллекций разных вельмож". В главе "О двенадцатом, почти сверхъестественном свойстве" речь идет о правильном икосаэдре - платоновом теле, ограниченном двадцатью правильными треугольниками.

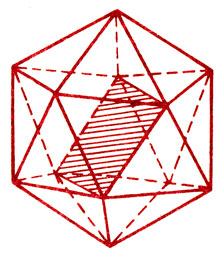
Вглядитесь повнимательнее в эту древнейшую игральную кость (13). К каждой вершине сбегаются пять треугольников, свободные стороны которых образуют уже знакомый нам правильный пятиугольник. Если же соединить между собой любые два противоположные ребра икосаэдра, то получится прямоугольник, тоже имеющий прямое отношение к "божественной" пропорции,- его большая сторона так относится к меньшей, как сумма сторон - к большей. И именно икосаэдр связан с математической знаменитостью - проблемой "целующихся сфер", которая возникла в споре Исаака Ньютона с оксфордским астрономом Дэвидом Грегори (4).

Великолепная пятерка

Наконец, в самые последние годы это звучное греческое слово вновь замелькало в научных статьях: выяснилось, что структура кристаллического бора - идеальный икосаэдр. И даже вирусы, которые раньше так и назывались "сферическими" - например, вирус полиомиелита,- и то, как удалось обнаружить, имеют форму икосаэдра. Но об этом чуть позже.

"Евклид вовсе и не собирался выпускать систематический учебник геометрии. он задался целью написать сочинение о правильных многогранниках, рассчитанное на начинающих, в силу чего ему пришлось изложить все необходимые сведения" - шутка известного английского естествоиспытателя и геометра д'Арси Томпсона, как и всякая хорошая острота, содержит зерно истины. Ведь согласно Проклу, Евклид считал венцом всех тринадцати книг своих "Начал" предложенные им способы построения пяти Платоновых тел - недаром он поместил их в последнюю, тринадцатую книгу. Строить, в его понимании, значило начертить, пользуясь только циркулем и линейкой.

Но прежде чем браться за правильные пространственные тела, Евклиду пришлось "изложить все необходимые сведения" о правильных плоских фигурах.

Великолепная пятерка

В первой книге "Начал" он учит, как строить правильный треугольник, а в четвертой - квадрат, пяти-, шести- и пятнадцатиугольник с равными сторонами и углами при вершине. Но вот правильный семиугольник ни Евклиду" ни его последователям построить не удалось, а пытались многие, потому что семиугольная звезда играла определенную роль в астрологии. Однако только в 1796 году Карл Фридрих Гаусс сумел выяснить, какие именно правильные многоугольники могут быть построены с помощью циркуля и линейки, а какие - никогда. Ему было тогда всего 19 лет, и он готовился стать филологом. Открытая закономерность произвела на Гаусса такое сильное впечатление, что он не только забыл и думать о филологии, и не только с головой ушел в математику, но и всю жизнь, уже став великим ученым, гордился своим юношеским успехом. И геттингенцы поставили ему памятник, в пьедестале которого правильный 17-угольник. Сограждане великого математика достойно почтили его память. Установленный Гауссом закон связывает между собой две самые могучие ветви математического древа - геометрию и теорию чисел. ("Математика - царица наук, теория чисел - царица математики",- писал Гаусс.) Закон этот гласит: циркулем и линейкой можно построить правильный n-угольник в том и только в том случае, если число его сторон n разлагается на простые множители, каждый из которых является так называемым "простым числом Ферма", и вдобавок множители эти не повторяются. (Единственное исключение - числа, кратные 2. Они могут, конечно, входить в состав множителей n - ведь нетрудно сколь угодно раз удвоить число сторон уже построенного многоугольника.

Великолепная пятерка

"Простые числа Ферма" выражаются простой формулой, придуманной Ферма: 2^2k+1. Вот первые пять таких чисел: 3, 5, 17, 257 и 65 537. Семерка не входит в их число, и потому астрологам придется самим строить свой символ.

В "Математической смеси", переведенной на русский язык книге Литлвуда, есть такая миниатюра:

"Один слишком навязчивый аспирант довел своего руководителя до того, что тот сказал ему: "Идите и разработайте построение правильного многоугольника с 65 537 сторонами". Аспирант удалился, чтобы вернуться через 20 лет с соответствующим построением". Это не совсем анекдот: некто О. Гермес действительно потратил десять лет на такой бессмысленный труд. Рукопись его, заключенная в большой ящик, до сих пор хранится в Геттингенском университете - памятником титанической усидчивости.

Великолепная пятерка

Счастье, что руководитель остановился на пятом простом числе Ферма. Возьми он шестое (а вычислить его не так уж трудно: 225+1 = 232+1 = 4 294 967 297), бедняга аспирант до конца своих дней не оторвался бы от чертежей. И дело не в гигантской величине числа сторон. Оказалось, что Ферма ошибался: "шестое простое число Ферма" не постое, а составное: оно разлагается на множители.

Доказать это удалось Леонарду Эйлеру.

"Эйлер... не проглядел ничего в современной ему математике, хотя последние 17 лет своей жизни он был совершенно слепым",- писал один известный историк математики. Не проглядел Эйлер и проблемы многогранников. Если бы Евклид и в самом деле хотел написать многотомное сочинение о Платоновых телах, ом все равно не мог бы сделать этого, не зная формулы Эйлера, с которой мы уже встречались. А ведь она даже проще, чем знаменитый "Понст асинорум" - "Мост для ослов", не преодолев который, нельзя, по мнению Евклида, считать себя разумным человеком (перейдите ради самоутверждения через него и вы: докажете, что углы при основании равнобедренного треугольника равны)! "Некоторые из его простейших открытий таковы,- писал про Эйлера Г. С. М. Коксетер, один из крупнейших современных геометров,- что можно представить себе дух Евклида, вопрошающий: "Почему при жизни на Земле я не додумался до этого?" Но когда слышишь именно эту формулу, то досада "почему не я?!" Невольно берет любого.

Великолепная пятерка

Послушайте:

"В любом простом выпуклом многограннике число вершин плюс число граней и минус число ребер равно двум".

Проверьте (еще раз):

на тетраэдре, кубе, октаэдре, на любой фигуре, которую способно измыслить ваше воображение,- с прямо- или криволинейными ребрами, с какими угодно гранями (только без "дыр" - это и значит "простой" многогранник).

Убедитесь (окончательно):

формула Эйлера В+Г-Р = 2 справедлива в любом случае.

Великолепная пятерка (12)

Эта прославленная формула не связана, как мы имели случай увериться, ни с расстояниями, ни с углами, она предельно наглядна. Она буквально видна в прозрачном воздухе геометрического сада. Но эта простота и наглядность - отражение фундаментальных свойств нашего трехмерного пространства. Именно из-за своей фундаментальности формула эта стала основой для двух математических дисциплин - топологии и теории графов.

Заставим же ее поработать и на нас - выясним, наконец, почему Платоновых тел пять, а не три или восемь.

"В геометрию нет царского пути!"- услышал Птолемей I, когда потребовал, чтобы Евклид обучил его своей науке как-нибудь побыстрее. А уж в наше время и вовсе нет иного способа понять некоторые геометрические вещи, кроме пристального размышления над ними. В этом и объяснение и оправдание тех крайне, впрочем, простых формул, к которым нам придется прибегнуть, чтобы ответить на только что поставленный вопрос. "Понимание математики не приобретается только безболезненно развлекательными способами",- писал Рихард Курант, крупный американский ученый, иностранный член нашей Академии наук, эмигрировавший в Америку из Германии, когда там к власти пришел Гитлер.

Правильный многогранник тем и правилен, что каждая грань его правильный р-угольник и в каждой вершине сходится одно и то же число q таких граней. (Математики обозначают это обстоятельство символом Шлефли - {p, q}) Отсюда следует, что число всех ребер, которые составляют "каркас" платонова тела (иными словами, число планок, которые пришлось заготовить Леонардо да Винчи для каждой из своих моделей), можно подсчитать двояким путем. Оно равно произведению числа всех вершин на число сходящихся к каждой из них ребер q, поделенному пополам,- ведь при таком подсчете мы каждое ребро учитываем дважды, по одному разу каждый его конец. Но, с другой стороны, те же ребра можно пересчитать Платонову телу и по-другому, помножив число его граней на число сторон каждой грани р и опять - по той же причине - разделив эту цифру на Два. Если подставить теперь полученные соотношения в формулу Эйлера и несколько поразмыслить над получившимся результатом, то мы как раз и докажем утверждение Евклида: Платоновыми телами могут быть лишь многогранники, символы Шлефли которых - {3,3}; {4,3}; {3, 4}; {5,3} и {3,5}. Итого-пять! Четыре из них Мауриц Эсхер соединил в удивительную конструкцию, внутреннюю часть которой составляет куб с прошедшим сквозь него октаэдром, а наружная "оболочка" - это взаимопроникшие икосаэдр (светлые треугольные грани) и додекаэдр (его грани более темные, пятиугольные). Называется эта конструкция "Стереометрические фигуры". Отсутствующий на ней тетраэдр художник изобразил на гравюре "Двойной планетоид". Там их даже целых два: один прошел сквозь другой, причем первый "цивилизован", а второй остался в первозданном, диком виде.

Великолепная пятерка (13)

"Только забавляясь и учатся",- считал Анатоль Франс. Известный ирландский ученый сэр Уильям Роуэн Гамильтон в 1859 году занялся математическим бизнесом: выпустил в продажу головоломку, состоящую из деревянного додекаэдра, в каждую из двадцати вершин которого вбит гвоздь с большой шляпкой, чтобы не соскакивала обернутая вокруг него веревка. Под каждым гвоздем стояло название крупного города - Дели, Филадельфия, Брюссель... Надо было продолжить веревочный маршрут, проходящий через все центры цивилизации точно по одному разу.

Очевидно, новый товар не вызвал ажиотажа на рынке, а изготовлять правильный двенадцатигранник не так просто, и потому Гамильтон предложил другой вариант игры - технологически намного упрощенный. Роль додекаэдра, пространственного тела, играло его плоское изображение - так называемый граф, то есть фигура, составленная из вершин, соединенных ребрами. (Все многоугольники, все мозаики, что мы рассматривали и еще только будем рассматривать,- это, несмотря на свой простецкий вид, типичные графы.)

Граф, заменяющий собой многогранник, повторяет его архитектуру - столько же вершин, столько же ребер и граней, тот же способ соединения их друг с другом. (Потому формула Эйлера, справедливая для многогранников, верна также и для графов.) Вот один из способов получить такой граф: надо спроецировать весь многогранник на плоскость одной из его граней, а центр проекции выбрать недалеко от ее середины. Тогда для пяти Платоновых тел получаются графы (см. 73-ю страницу книги). Они называются диаграммой Шлегеля. Таким нам увиделся бы гигантский многогранник, если бы мы удалили одну его грань, забрались в образовавшуюся дыру и стали рассматривать его изнутри. Диаграммы эти очень удобны - они позволяют на листе бумаги производить манипуляции с объемным телом, чем и воспользовался Гамильтон, чтобы упростить свою нерентабельную головоломку.

Математика сохранила память о его поучительной игрушке - до сих пор линия, проходящая по одному разу через все вершины графа, называется гамильтоновой. Но и сейчас никто не может сказать, существует ли для того или иного графа гамильтонова линия или нет. А это весьма обидно, ибо жизнь часто требует ответа на подобный вопрос. Например, знаменитая "задача о странствующем торговце" состоит в том, что он должен посетить несколько городов и как можно скорее вернуться домой. В общем виде эта транспортная проблема не решена. Можно, конечно, перебрать все варианты и выбрать наилучший порядок обхода городов, но если их много, за дело без мощных вычислительных машин лучше не браться. Впрочем, кое-какие задачи подобного типа все-таки решены - например, найдена кратчайшая авиалиния, проходящая по всем главным городам Америки.

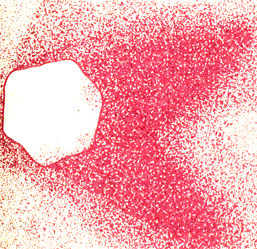
"Со времен древнегреческих философов правильные многогранники считались не более, чем игрушкой для математиков, не имеющей никакого практического значения. весьма замечательно, что как раз эти фигуры оказались в центре внимания биологов в их яростных спорах относительно точной формы вирусов",- замечает в своей превосходной книге "Нить жизни" крупнейший специалист в области структуры белка Джон Кендрью - тот самый, который сумел определить пространственную конфигурацию молекулы миоглобина, за что и получил Нобелевскую премию. В этой книге помещена чрезвычайно любопытная фотография вируса, поражающего комара-долгоножку, так называемого иридесцентного вируса Tipula (14). До того, как его сфотографировали под электронным микроскопом, на вирус этот с двух разных сторон направляли атомы металла. Поэтому позади него образовались своего рода "тени". И вот этот метод двойного напыления позволил разглядеть на фотографии, что тени имеют острые Углы! Значит, вирус не может быть совершенно кругам, как считалось ранее. Чтобы установить точную его форму, брали различные многогранники и направляли на них свет под теми же углами, что и поток атомов металла на частицу вируса. Оказалось, что только один многогранник дает точно такую же тень. Имя его - икосаэдр.

Великолепная пятерка (14)

Послушайте Джона Кендрью:

"Вы можете спросить: а почему обязательно правильный многогранник? И почему именно икосаэдр? По-видимому, тут все дело в экономии - экономии генетической информации. Вирусная частица должна весь обмен клетки-хозяина перевернуть вверх дном; она должна заставить зараженную клетку синтезировать многочисленные ферменты и другие молекулы, необходимые для синтеза новых вирусных частиц. Все эти ферменты должны быть закодированы в вирусной нуклеиновой кислоте. Но количество ее ограничено. Поэтому для кодирования белков собственной оболочки в нуклеиновой кислоте вируса оставлено совсем мало места. Что же делает вирус? Он просто использует много раз один и тот же участок нуклеиновой кислоты для синтеза большого числа стандартных молекул - строительных белков, объединяющихся в процессе автосборки вирусной частицы. В результате достигается максимальная экономия генетической информации. Остается добавить, что по законам математики для построения наиболее экономичным способом замкнутой оболочки из одинаковых элементов нужно сложить из них икосаэдр, который мы наблюдаем у вирусов".

Так "решают" вирусы сложнейшую (ее называют "изопиранной") задачу: найти тело наименьшей поверхности при заданном объеме и притом состоящее из одинаковых и тоже простейших фигур. Вирусы, мельчайшие из организмов, настолько простые, что до сих пор неясно - относить их к живой или неживой природе,- эти самые вирусы справились с геометрической проблемой, потребовавшей у людей более двух тысячелетий! Все так называемые "сферические вирусы", в том числе такой страшный, как вирус полиомиелита, представляют собой икосаэдры, а не сферы, как думали раньше.

Эта внушительная и в то же время удивительно целесообразная конструкция, состоящая из двадцати простейших одинаковых деталей - правильных треугольников - и заключающая внутри себя наибольший возможный объем, вновь наталкивает на мысль об изначальной простоте Природы. Она строит все свое богатство и разнообразие из простейших блоков. Недаром же Джон Кендрью назвал вирусы "живой архитектурой". В свете последних научных достижений платоновский четырехэлементный мир не кажется больше таким уже абсурдным. И вслед за Адельбертом Шамиссо, немецким поэтом и ученым, хочется повторить полушутливые слова: "Во мгле веков перед нашим взором блеснула истина. Она, как теорема Пифагора, до наших дней еще верна".

Великолепная пятерка (15)

Истина эта, как стало ясно в последнее время, связана с так называемым экстремальным свойством правильных многогранников. То есть с их способностью ограничивать собою объем больший, чем любое другое тело с тем же числом граней. Или же, что то же самое, иметь наименьшую поверхность среди всех тел с тем же объемом и числом сторон. Правильные многогранники в некотором смысле самые "выгодные" фигуры. Природа пользуется этим фактом шире, чем нам думалось.

"На разных этапах развития математики вплоть до настоящего времени геометры возвращались к теории выпуклых многогранников и открывали в ней новые фундаментальные факты",- писал Лазарь Аронович Люстерник, член-корреспондент нашей Академии наук. Один из таких глубоких фактов и есть экстремальное свойство правильных многогранников. Проблема эта уходит корнями в седую древность.

...Финикийская царица Дидона отличалась невероятной прозорливостью - она предугадывала, что Марку Катону Старшему надо будет чем-то заканчивать каждую из своих речей в сенате, и ради этого решила основать Карфаген. Кроме того, Дидона была еще жадной и тщеславной, поэтому ей хотелось, чтобы новый город занимал как можно больше места на земле. Но она же вдобавок обладала хитростью и поразительной геометрической интуицией, и только благодаря этому удался ее честолюбивый замысел. В обмен на ничтожные безделушки Дидона выторговала у вождей племен, населявших север Африки, право владеть "клочком земли, который покроет воловья шкура". Коварная финикийская царица и не думала класть шкуру на землю - нет, она разрезала ее на тонкие ремни, связала их вместе и этой длинной веревкой вознамерилась огородить свое будущее владение. И тут перед ней - впервые за всю человеческую историю - встала задача, которую много веков спустя назовут изопериметрической: какую форму должна иметь замкнутая линия, чтобы площадь, заключенная внутри нее, получилась наибольшей?

Догадалась ли Дидона, что искомая фигура - круг? Кто знает... Известно лишь, что легендарная царица и на этот раз сумела урвать лишний кусок - она выбрала свой участок на берегу моря, так что вся морская граница досталась ей даром. За этой женщиной придется признать крупный геометрический талант: ведь изопериметрическая задача строго была решена лишь в прошлом веке швейцарским геометром Якобом Штейнером, а ее "карфагенский вариант" - с учетом того, что часть замкнутой кривой представляет собой прямую линию "побережья",- и того позже.

Штейнер доказал - притом сразу пятью разными способами,- что именно круг охватывает самую большую площадь при данной длине замкнутой линии. Вслед за этим удалось выяснить, что следующее слово за правильными многоугольниками: они "выгоднее" любой другой фигуры с тем же числом сторон. Так была окончательно решена задача, которой, кроме легендарной Дидоны, занимались реальные ученые - например, Зенодор и Архимед. Но тут же возникла новая: а какое пространственное тело может ограничить наибольший объем при той же поверхности? Или же какую форму должна иметь наименьшая поверхность, заключающая в себе данный объем? Ответ на оба вопроса почти очевиден: шар. Но что дальше? Кто следующий претендент на решение изопиранной (так она называется) задачи?

Да, правильные многогранники. Они обладают - среди всех прочих фигур с тем же числом граней - экстремальными свойствами. Это предположение тоже принадлежит Штейнеру.

Но правильные многогранники разные: тетраэдр, октаэдр и икосаэдр составлены из треугольных граней, куб ограничен квадратами, додекаэдр - пятиугольниками. У тетраэдра - всего четыре грани, у куба - шесть, октаэдра - восемь, додекаэдра - двенадцать, а у икосаэдра - все двадцать.

Значит, среди самих Платоновых тел существует конкуренция? Да, и фаворит в ней "многосторонний" икосаэдр. Вот его-то исключительностью среди всех пяти героев нашего рассказа и воспользовались вирусы.

"Живые источники математического творчества неотделимы от интереса к познанию природы и задачам управления природными явлениями",- утверждает академик Андрей Николаевич Колмогоров. "Числа не управляют миром, но показывают, как управляется мир" - так переработал пифагорианскую мудрость, избавив ее от идеалистического звучания, Иоган Вольфганг Гёте. Мысль о том, что в первооснове вещей лежат некие простые математические соотношения, крепко пустила корни на нашей планете и часто являлась в гениальные головы, перелетая через тысячелетия и континенты.

Кристаллы в виде кубов, тетраэдров и октаэдров, вирусы, ныне обретшие икосаэдрическую форму,- все это, очевидно, далеко не последние шаги наглядных математических представлений в глубины нашего мира.

Впрочем, почему только "в глубины"? Почему речь все время идет лишь о свойствах вещества? Зачем забывать о додекаэдре - платоновском символе Вселенной, "пятой сущности" алхимиков?^* Если справедлив платоновский принцип: "геометрия приближает разум к истине", то он верен не только в микро-, но и в макрокосмосе. Числа все-таки должны править миром - описывать законы движения Вселенной.

^* ("В запасе осталось еще пятое многогранное построение,- пишет Платон в "Тимее",- его бог определил для Вселенной и прибегнул к нему, когда разрисовывал и украшал ее".)

"Геометрия древних греков стала краеугольным камнем новой астрономии" - это известное изречение больше всего относится к астрогеометрическим экспериментам Иоганна Кеплера. Открыв основные законы движения планет нашей Солнечной системы, он задался следующим вопросом: а почему они находятся на том или ином расстоянии от Солнца? И тут сказалась приверженность Кеплера к "чистой геометрии". "Если бы небесные движения были произведениями разума, можно было бы с основанием заключить, что орбиты планет - совершенные круги... сам Господь, который был слишком благ, чтобы оставаться праздным, затеял игру в символы, посылая знаки своего подобия в мир. Поэтому и я осмеливаюсь думать, что вся природа и благословенное небо записаны на языке искусства геометрии". Ясно, что человек с такой идеологией должен видеть торжество геометрии во всем, в том числе и во Вселенной. Кеплер пытался найти смысл в расположении планетных орбит, вписывая правильные многоугольники в окружности, а сферы - в кубы, последовательно, одну за другой, все уменьшая их размер. Но никакой аналогии с распределением планет на небесах не возникало.

И вдруг Кеплера осенило. Планет всего шесть и, следовательно, промежутков между ними - пять. Но и Платоновых тел тоже пять - не больше и не меньше. Не может быть, чтобы это совпадение оказалось случайным! И Кеплер стал лихорадочно вставлять один правильный многогранник в другой, по-разному комбинируя их и вписывая в каждый сферу,- математический прообраз планетных орбит. К его радости, эти построения, легшие в основу его книги "Тайна Вселенной" (в других переводах - "Космографическая тайна" и "Тайна мироздания"), обнаружили определенное сходство с небесным порядком, каким он виделся астрономам в те годы. "Несравненное удовольствие, которое я испытал от этого открытия, невозможно выразить словами",- писал он. В книге Иоганна Кеплера есть чертеж (15), из которого видно, каким он представлял себе механизм, ведающий размещением планет. Вокруг Солнца описан самый большой шар, по нему движется Сатурн. Теперь в него надо вписать куб, а в куб этот - снова шар, который определит собой орбиту Юпитера. Если в этот меньший шар вписать тетраэдр, а в него опять шар, то получится орбита Марса. Так, следуя Кеплеру, и надо продолжать вписывать в шары правильные многогранники, а в них - снова шары. Между Марсом и Землей окажется додекаэдр, между Землей и Венерой - икосаэдр, а Венеру и Меркурий разделит октаэдр. Точные значения орбит у Кеплера не получались, но он считал, что есть разница между "мыслимой идеей круга и действительным путем планеты", поскольку "небесные движения - произведения не разума, а природы". Поэтому ему пришлось подправлять свою модель - шары на его чертеже имеют различную толщину. Но все это было бы ничего, если бы не открыли новые планеты, а запас Платоновых тел, разумеется, не пополнился: их как было, так и осталось пять.

"Погоня за идеей - занятие столь же захватывающее, как и погоня за китом",- писал Генри Норрис Рассел. Он не мог, конечно, сбросить со счетов те случаи, когда кит срывается с гарпуна. Построение Кеплера рухнуло, но сами поиски геометрической целесообразности устройства мира не становятся от этого менее привлекательными. В саду геометрии все видно, все наглядно - ветви в нем не спрятаны под листвой недоступных формул и абстрактных идей.

Но они переплетены. Вписывая, по-кеплеровски, правильные многогранники в сферу, мы не только создаем красивое построение, но и вторгаемся в новую область нашей "многогранной" темы. О том, что случается, когда правильный многогранник вписывают в сферу - о сферических мозаиках, о математических мозаиках вообще, которые есть не что иное, как вырожденные многогранники, - речь пойдет дальше. А пока - лишь один взгляд на гравюру М. К. Эсхера "Колючий цветок": его лепестки так же переплетены, как и геометрические проблемы, очередь которых впереди.

Великолепная пятерка

Мой дорогой отец!.. Как поживают 
травы, кустарники и деревья? 
Коровы, овцы, лошади, собаки 
и люди?.. Я сделал тетраэдр, 
додекаэдр и еще два эдра, 
для которых не знаю 
правильного названия.

Джеймс Клерк Максвелл