II. Мебиусиана

Геометрия есть познание всего 
сущего.

Платон

Мебиусиана

"Униформа, по местам! Маэстро, туш!"- на арене фокусник. Его инструментарий прост до крайности - горизонтальная перекладина на двух стойках, в которую вбито несколько гвоздей, и на каждом из них висит по длинной яркой ленте. Все самое простое и настоящее - любой желающий волен убедиться в этом собственноручно. Маг закуривает сигарету и горящим концом дотрагивается до первой ленты. Пламя бежит вдоль нарисованной посередине ленты дорожки, вызывая восхищение малышей. Но вот огненное кольцо замкнулось - и тут уж крик удивления вырывается у взрослых: вместо ожидавшихся двух тонких лент появляется одна длинная. Прикосновение сигареты к другой ленте - снова взрыв детского восторга и за ним озадаченное молчание взрослых: теперь перед ними две ленты, продетые одна в другую. Еще одна огненная дорожка - и лента делает еще один неожиданный вольт: теперь она завязывается узлом.

Мебиусиана

Детская радость понятна - им неведомо, что на свете бывают химики и что они придумали калиевую селитру. Но и недоумение родителей тоже идет от незнания - топологии вообще и одной из ее излюбленных игрушек, "листа Мёбиуса", в частности.

А игрушка эта полюбилась математикам, и не им одним. У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка. В 1967 году, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена все та же лента. И монумент высотой более чем в два метра, и крохотная марка - своеобразные памятники немецкому математику и астроному Августу Фердинанду Мёбиусу, профессору Лейпцигского университета.

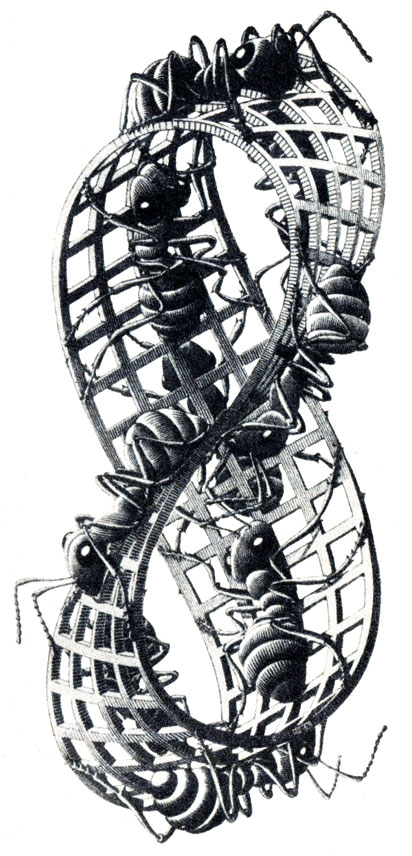
В своей работе "Об объеме многогранников" он описал геометрическую поверхность, обладающую совершенно невероятным свойством: она имеет только одну сторону! Самое же при этом удивительное, пожалуй, то, что сделать ее своими руками не представляет решительно никакого труда: надо лишь взять полоску бумаги и склеить ее концы, предварительно повернув один из них на 180 градусов. И тогда в ваших руках окажется лист, или лента, Мёбиуса. Чтобы наглядно убедиться, что у вашей самоделки действительно всего одна сторона, попробуйте закрасить перекрученную ленту в два цвета - одним с внешней, а другим - с внутренней стороны. Что бы вы ни придумывали, вам это не удастся. Но зато муравью, ползущему по листу Мёбиуса, не надо переползать через его край, чтобы попасть на противоположную сторону, как это видно на гравюре Маурица Эсхера "Лента Мёбиуса. II".

Итак, односторонность. В геометрическом, разумеется, понимании этого слова, потому что в нашем общечеловеческом смысле трудно представить себе более разностороннюю геометрическую фигуру. Теперь, когда вы познакомились с ней, наверное, уже никакая сила не Удержит вас от того, чтобы не клеить все новые и новые ленты, закручивая их то на один, то на два, а то и на три полуоборота, и потом беспощадно разрезать вдоль. И вы будете вознаграждены за свою любознательность - полоска бумаги повторит все фокусы, показанные в Цирке.

Да что цирк! Патентные службы вынуждены были познакомиться с поразительными свойствами листа Мёбиуса - в разное время и в разных странах зарегистрировано немало изобретений, в основе которых лежит все та же односторонняя поверхность. В 1923 году знаменитый американский изобретатель Ли де Форест, который придумал трехэлектродную лампу - триод, предложил записывать звук на киноленте без перемены катушек, сразу "с двух сторон". Ему выдали патент № 1442632. Изобрели магнитофон - и сразу же нашлись сообразительные люди, которые придумали особые кассеты, где магнитная лента соединяется в кольцо и перекручивается. Ясно, что тогда можно записывать и считывать подряд с двух дорожек, не снимая кассеты с магнитофона и не меняя их местами, а значит, время непрерывного звучания увеличивается ровно вдвое. (Речь идет, разумеется, о так называемой "непрерывной ленте", то есть замкнутой в кольцо, вроде автоматических телефонных часов или милицейских лозунгов о безопасности движения, передаваемых через репродукторы, патрульных машин.) В 1969 года советский изобретатель А. Губайдуллин получил авторское свидетельство № 236278 на бесконечную шлифовальную ленту, работающую обеими своими сторонами. Он предложил натянуть сделанную из специального материала ленту Мёбиуса на два вращающихся ролика и покрыть ее крупинками твердого абразива. Понятно, что такая лента служит вдвое больше обычной. Ту же идею использовали сотрудники НИИ автоматизации черной металлургии Г. Буйный и В. Изотов в своем устройстве для магнитной дефектоскопии (им выдано авторское свидетельство № 259449).

Идея использовать ленту Мёбиуса не оставляла изобретателей и в последующие годы. В 1971 году П. Н. Чесноков из Уральского политехнического института имени С. М. Кирова получил авторское свидетельство на фильтр непрерывного действия для жидкости, "отличающийся тем, что, с целью интенсификации процесса фильтрования и увеличения срока службы фильтрующего материала, лента выполнена в виде Мёбиуса листа". Год спустя И. В. Киселев стал официально автором устройства, про которое в авторском свидетельстве сказано: "Бесконечный шлифовальный ремень, выполненный на гибкой основе с нанесенным на нее абразивным покрытием и склеенный в кольцо с повернутой ветвью, отличающийся тем, что, с целью увеличения стойкости, он имеет в сечении форму многогранника с равными гранями, покрытыми абразивным слоем, а ветвь его повернута на одну грань". Институт электродинамики Академии наук Украинской ССР представил изобретение своих сотрудников Ю. И. Драбовича и И. А. Криштафовича. Оно сформулировано так: "Магнитный сердечник, изготовленный из ферромагнитной ленты с изоляционным покрытием, отличающийся тем, что, с целью улучшения магнитных свойств сердечника путем создания равномерного магнитного поля по его сечению, сердечник намотан в форме ленты Мёбиуса".

Наконец, не были забыты и дети, для которых И. Е. Бурлак изобрел и получил на то в 1979 году соответствующее свидетельство, в котором в тех же строгих правилах заявки описана "игрушечная электрифицированная железная дорога, содержащая полотно железной дороги, модели локомотива и вагонов с поворотными осями колес, отличающаяся тем, что, с целью повышения занимательности, полотно железной дороги представляет собой ленту Мёбиуса, рельсы выполнены из ферромагнитного материала, а модели локомотива и вагонов снабжены магнитными башмаками, закрепленными на поворотных осях колес".

В 1963 году патентное ведомство США зарегистрировало два "практически геометрических" изобретения. Некто Джакобс поставил свои знания топологии на службу химчистке - он придумал самоочищающийся фильтр, который представляет собой все ту же ленту Мёбиуса и беспрерывно освобождается от впитанной грязи, работая при этом обеими своими сторонами. А Ричард Дэвис, физик из американской корпорации "Сандиа" в Альбукерке, изобрел электрическое сопротивление, обладающее нулевой реактивностью. О нем, пожалуй, стоит поговорить поподробнее и потому, что такое сопротивление - давнишняя мечта радиотехников и физиков, и потому еще, что тут нам предоставляется возможность увидеть нашу одностороннюю ленту Мёбиуса с несколько иной стороны.

Но сначала склейте еще один лист Мёбиуса и разрежьте его ножницами вдоль не на две, а на три части, то есть не посередине, а отступив от любого из краев на треть ширины ленты. Нечто похожее изобразил Мауриц Эсхер на гравюре "Лента Мёбиуса. I". Вас снова ждет сюрприз: теперь получается еще один лист Мёбиуса - поменьше, да и толщиной всего в треть от первоначального! а в него продета длинная и тонкая лента, дважды перекрученная вдоль своей оси. А теперь сделайте себе из всего этого геометрического изобилия прекрасную игрушку на вечер - другой. Это, как и все предыдущее, просто. Покрасьте "маленького Мёбиуса" в какой-нибудь цвет. И попытайтесь уложить с обеих сторон от него ленту так, чтобы получился лист Мёбиуса тройной толщины.

Рано или поздно вы справитесь с задачей, и наградой вам будет удивительная фигура. Две ее крайние незакрашенные части, хотя они и сделаны из одной длинной ленты, тем не менее нигде не смыкаются друг с другом, а просто лежат вдоль сторон третьей, закрашенной. Но каких сторон? Ведь центральная часть - это односторонняя поверхность! Да и крайние, раз они повторяют ее форму, тоже не что иное, как два листа Мёбиуса, которые обрели самостоятельность, обвившись вокруг своего цветного собрата.

Вот это и есть сопротивление с нулевой реактивностью. Но только изготовляют его - для простоты технологии - немного по-другому: к резиновой ленте с двух сторон приклеивают две тонкие алюминиевые полоски, а к ним припаивают выводы, через которые можно подать электрический ток. Затем всю конструкцию перекручивают на один оборот и соединяют в мёбиусов лист - он, естественно, будет трехслойным. И вот теперь ток, проходя по полоскам, встретит на своем пути лишь так называемое "активное" сопротивление, то есть сопротивление самого материала - алюминия. "Реактивность" проводника с током, имеющего форму листа Мёбиуса, равна нулю.

Мебиусиана

"То, что я понял, прекрасно, из этого я заключаю, что остальное, чего я не понял, тоже прекрасно",- высказался в свое время Сократ по поводу неясностей у Гераклита. Быть может, эти слова послужат неким утешением для того, кто не сумеет одолеть суть радиотехнического дебюта листа Мёбиуса. Хотя понять ее не так уж невозможно. Есть простой, но в данном случае неприятный для радиотехников факт: каждое тело имеет форму и как-то располагается в пространстве. А потому оно ведет себя либо как маленький конденсатор - обладает собственной электрической емкостью и, значит, оказывает переменному току емкостное сопротивление, либо поступает подобно крохотному дросселю - тогда его сопротивление индуктивное. Оба эти сопротивления, оказываемые телом электрическому току, называют реактивными. И избавиться от них, как и от того, что у него есть какая-то форма, ни одно тело как будто не может.

А теперь вспомним факт, в котором нам только что пришлось убедиться: "трижды толстый мёбиус" можно сделать по-разному - и из трех отдельных частей, и всего из двух: короткой центральной и особым образом уложенной длинной заготовки, которая одна образует обе боковые стороны. Значит, ток в безреактивном сопротивлении дважды проходит по одному и тому же месту в пространстве, но оба раза в противоположных направлениях, пробегая по длинной ленте - алюминиевым полоскам, уложенным "восьмеркой" с двух сторон короткой резиновой полосы, служащей изолятором. Таким образом, реактивность реактивностью же и уничтожается. И потому такое закрученное сопротивление остается чисто активным, даже если изгибать его как угодно или помещать в любое внешнее поле.

Конечно, радиотехники должны быть особенно благодарны Августу Фердинанду Мёбиусу - ведь им приходится иметь дело с миллионами герц, а чем выше частота, тем больше "реактивность" каждого элемента схемы и тем больше помех вносят в ее работу нынешние "нечисто активные" сопротивления. Но, пожалуй, с еще большим энтузиазмом встретят новое изобретение физики, которые занимаются сверхпроводимостью. Как известно, при очень низких температурах, близких к абсолютному нулю, сопротивление электрическому току вдруг пропадает и он может течь неограниченно долго, не требуя никакого притока энергии извне. Да, но речь идет об активном сопротивлении. Реактивное же сопротивление сверхнизкой температурой и всей невероятно сложной техникой, созданной для ее получения, не уничтожается. Зато простейшее геометрическое преобразование обещает физикам скорую и неожиданную помощь. Быть может, мечта о вечном электрическом двигателе, не требующем никакой энергии для своей работы, теперь уже близка к своему осуществлению...

Но до сих пор речь шла всего об одном свойстве листа Мёбиуса - о его односторонности. А ведь у него есть еще и другие подобные свойства. Но какие подобные? Математик назвал бы их топологическими.

Сама топология, можно сказать, началась именно с листа Мёбиуса. Слово это придумал Иоганн Бенедикт Листинг, профессор Геттингенского университета, который - и это далеко не всем известно - почти в то же время, что и его лейпцигский коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам единожды перекрученную ленту. Наука та молодая и потому озорная. Иначе не скажешь о тех правилах игры, которые в ней приняты. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать - делать с ней что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло - все ее свойства остались неизменными. Для него не имеют никакого значения ни расстояния, ни углы, ни площади. А что же его интересует? Самые общие свойства фигур, которые не изменяются и при каких преобразованиях, если только не случается катастрофы - "взрыва" фигуры. Потому иногда топологию называют "геометрией непрерывности". Она известна и под именем "резиновая геометрия", потому то топологу ничего не стоит поместить все свои фигуры на поверхность детского надувного шарика и без конца менять его форму, следя лишь за тем, чтобы шарик ie лопнул. А то, что при этом прямые линии, например стороны треугольника, превратятся в кривые, для тополога глубоко безразлично.

"Сотри случайные черты, и ты увидишь - мир прекрасен",- писал Александр Блок. Тополог всегда готов внять подобному призыву - во всех окружающих его предметах он ищет некие важные только ему одному качества. Например, непрерывность. Это еще одно топологическое свойство. Если вы сравните схему самолетных маршрутов и географическую карту, о убедитесь, что масштаб Аэрофлотом далеко не выдержан - скажем, Свердловск может оказаться на полпути от Москвы до Владивостока. И все-таки что-то общее между географической картой и топологической схемой (а транспортники - бессознательные топологи) есть. Москва действительно связана со Свердловском, а Свердловск - с Владивостоком. И потому тополог может как угодно деформировать карту, лишь бы точки, ранее бывшие соседями, оставались одна подле другой и дальше. А значит, с топологической точки зрения круг неотличим от квадрата или треугольника, потому что их легко преобразовать один в другой, не нарушая непрерывности. Взгляните с этой точки зрения на нашего старого знакомца и увидите: на листе Мёбиуса любая точка может быть соединена с любой другой точкой. И при этом муравью на гравюре Эсхера ни разу не придется переползать через край "ленты". Разрывов нет - непрерывность полная.

Но куда интереснее другое свойство - связность. Если квадрат полоснуть бритвой от стороны к стороне, то он, естественно, распадается на два отдельных куска. Точно так же любой удар ножом разделит яблоко на две части. Но вот чтобы располовинить кольцо, нужно уже два разреза. И два раза придется резать бублик, если вы хотите угостить им двух друзей. А телефонный диск можно десять раз рассечь ножом от одной замкнутой кривой до другой, а он все останется единым целым. Поэтому любой тополог скажет вам, что квадрат и ромашка - односвязны, кольцо и оправа от очков - двусвязны, а всяческие решетки, диски с отверстиями и подобные сложные фигуры - многосвязны. Ну а наш лист Мёбиуса? Конечно, двусвязен, ведь фокус в том и состоял, что, будучи разрезан вдоль, он превращался не в два отдельных кольца, а в одну целую ленту. Впрочем (и на этом тоже были построены фокусы), если перекрутить ленту на два оборота, то лист становится односвязным. Три оборота - помните ленту, завязавшую саму себя в узел?- связность снова равна двум. А четыре оборота? Да вы, верно, уже догадались, как дальше станут развиваться события.

Связность принято оценивать числом Бетти, названным так в честь известного итальянского математика и физика. Иногда пользуются другой величиной - эйлеровой характеристикой - с той же целью: определить число сквозных, от края и до края, разрезов, которое выдерживает фигура, не распадаясь при этом на части,

"От края и до края..." - эти слова из песни, любимой нами с детства, можно рассматривать не просто как поэтический образ. В них, как мы видим, заложен еще и глубокий топологический смысл. Лист бумаги - модель двусторонней односвязной (число Бетти равно единице) поверхности с одним краем. Его можно смять и бросить в урну, но все равно число краев (и сторон) останется прежним. Но у сферы краев нет. Нет их и у тора, говоря попросту, бублика. Зато нарисованное на бумаге кольцо имеет целых два края. Один край и у мёбиусова листа, как одна у него сторона. И снова - сделайте его из какой угодно эластичной резины и растяните до любых размеров - топологические свойства, этот незыблемый фундамент самого естества геометрической фигуры, останутся неизменными.

Мебиусиана (10)

Не много ли неожиданных и странных свойств? Тогда еще только два, быть может, самых любопытных.

Первое - ориентированность. Конечно, можно было бы подробно рассказать, что это такое. Но лучше дать определение "от противного": это то, чего нет у листа Мёбиуса! Вообразите, что в нем заключен целый плоский мир, где есть только два измерения, а его обитатели - несимметричные рожицы, не имеющие, как и сам лист, никакой толщины. Если эти несчастные создания пропутешествуют по всем изгибам листа Мёбиуса и вернутся в родные пенаты, то с изумлением обнаружат, что превратились в свое собственное зеркальное отображение. Конечно, все это случится только, если они живут в листе, а не на нем.

Впрочем, это удивительное явление можно наблюдать и на действующей модели плоского мира Мёбиуса - для этого надо сделать ленту из любого прозрачного материала.

Мебиусиана (11)

И наконец, то, что носит название "хроматический номер". Он равен максимальному числу областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Если каждую такую область выкрасить по-разному, то любой цвет должен соседствовать с любым другим. Так вот, на листке бумаги, даже если его склеить в кольцо, еще никому не удалось расположить пять цветных пятен любой формы, которые имели бы всеобщую границу. И на сфере, и на цилиндре их может быть не более четырех. Это и значит, что хроматический номер этих поверхностей - четыре. А на бублике число соседствующих цветов равняется семи. Каков же хроматический номер листа Мёбиуса? Он, как это ни поразительно, равен шести.

Конечно же, такое не укладывается в голове. Ну в самом деле, не довольно ли этих мёбиусовских мистификаций? Видите ли, на ленте, склеенной, как положено, размещается всего четыре цвета, а стоит соединить ее концы шиворот-навыворот - и непонятно, как находится место еще для двух цветов! Но клин выбивают клином, одну головоломку - другой. Есть древняя неразрешимая задача. Надо соединить три дома с тремя колодцами, но так, чтобы жители каждого из домов могли ходить по воду в любой колодец и при этом пути их нигде не пересекались. Сделать этого не умудрился никто, но лишь сравнительно недавно математики строго доказали, что задача неразрешима (неразрешима на плоскости, а на торе, то есть бублике, например, все получается просто). А теперь взгляните на рисунок (10). Если склеить эту полоску бумаги так, чтобы совпали одинаковые буквы на ее краях, то проблема водоснабжения решается. Разумеется, вы снова получите все тот же лист Мёбиуса. А теперь раскрасьте карту путей водовозов - и вот вам шесть цветов, живущих в дружном соседстве. Но, конечно, как и раньше, надо предполагать, что все события происходят не на листе, а внутри него. Иными словами, краски должны проникать сквозь бумагу, как чернила сквозь промокашку.

И напоследок возьмите еще раз в руки лист Мёбиуса - одностороннюю неориентированную поверхность с одним краем, числом Бетти, равным двум, и хроматическим номером, равным шести. Этот листок бумаги открыл математикам мир новых возможностей, а вам доставил несколько приятных минут. Но не спешите с благодарностью прощаться с ним. Он нам еще встретится - в космических далях Вселенной.

...У Фридриха Дюрренматта, в его нашумевшей в свое время пьесе "Физики", трое абсолютно здоровых ученых сознательно изображают из себя сумасшедших. Весь персонал дома умалишенных обращается к ним не иначе как "господин Ньютон", "господин Эйнштейн" и "господин Мёбиус". Разумеется, фантазия драматурга могла поместить в столь экзотические обстоятельства и других каких-либо прославленных ученых - тем более, что Мёбиус не такой уж физик, каким он, видимо, казался Дюрренматту. И все-таки выбор его не выглядит случайным. Вселенная Эйнштейна сменила вселенную Ньютона благодаря тому, что удалось постичь некую глубокую внутреннюю закономерность, свойственную природе. Вселенная Мёбиуса... Нет, конечно, ее не было, нет и, наверное, не будет. Но мёбиусианские идеи касаются настолько интимных свойств нашего мира, что они просто не имеют права как-то не проявить себя в грядущих фундаментальных исследованиях.

Мебиусиана

Математика есть способ 
называть разные вещи 
одним именем.

Анри Пуанкаре