Игра Го

Го - одна из самых древних и мудрых игр в истории человечества. Но в нашей стране она только недавно начала завоевывать популярность - открываются клубы, проводятся турниры, в спортивных магазинах можно приобрести комплект игры. Любопытно мнение о Го шахматного короля Эм. Л аскера: "Эта игра простотой правил превосходит шахматы, не уступая им богатством фантазии". В журнале "Наука и жизнь" публиковался содержательный материал по Го вместе с многочисленными задачами, но в книгах, изданных на русском языке, игра до сих пор не освещалась.

Игра Го

Несмотря на афористическое высказывание Ласкера, игра Го не столь уж проста, и автор книги не рискнул бы вести рассказ о ней без спарринг-партнера. Глава эта написана при активном участии математика и сильного московского игрока А. Гончарова, занимающегося разработкой программы для Го на компьютере.

Исторические сведения. Судя по археологическим находкам, игра Го родилась четыре тысячи лет тому назад. Густой туман времени скрыл от нас тайны ее появления. Хотя игра эта старинная, но по проблемам, которые она ставит нашему интеллекту, Го представляется весьма современной. Траектория ее распространения, охватившая страны Востока, ныне протянулась почти по всему Западу.

Первоначально Го (под теми или иными названиями) применялась как инструмент астрологии. Согласно гороскопу человека, желавшего узнать свое будущее, на доске (небе) расставлялись камни (звезды). Белые камни символизировали добро, а черные - зло. Начиналась "игра" с собственной судьбой. В такой необычной для нас форме выражался тот факт, что каждый человек сам творец своей судьбы. Постепенно Го вышла из астрологических пеленок и из мистической игры превратилась в игру интеллектуальную.

К первому тысячелетию до нашей эры Го стала модной в императорских кругах и приравнивалась к признанным в те времена искусствам каллиграфии и аранжировки цветов. После того как игра привлекла внимание Конфуция, все восточные мудрецы сочли достойным серьезно заниматься ею.

Бурным развитием Го отличался XVII век, когда молодой японский монах Хонинбо Санса покинул буддийский монастырь и возглавил первую государственную академию Го. Получив возможность целиком посвятить себя искусству Го, лучшие игроки того времени стали образовывать школы Го со своими лидерами и стилями игры. Японская школа Хонинбо в течение трехсот лет была сильнейшей в мире, и, наверное, поэтому Го обычно связывают с Японией, иногда называя игру японскими шашками.

Интерес к игре продолжает расти, в настоящее время в Го-клубах Японии зарегистрированы миллионы членов, издаются книги, журналы, проводятся многочисленные соревнования. Состоялось уже шесть чемпионатов мира среди любителей. В последнем из них участвовали представители более сорока стран. Профессионалы проводят свои турниры отдельно. В СССР тоже имеется много сильных игроков, и лучшие из них на равных сражались с японскими мастерами Го, посетившими несколько раз нашу страну.

Квалификационная шкала в Го отличается от шахматной. Вместо разрядов и званий используются кю и даны. Самая нижняя ступенька - 20-й кю, за ним идет 19-й и т. д. до первого. Далее присваиваются даны - от первого до девятого. Для того чтобы двум игрокам разной силы было интересно играть между собой, применяется система гандикапа, то есть в зависимости от разницы в силе игры более опытный игрок дает партнеру фору несколько камней, которые тот ставит на доску перед началом партии. Можно продолжить разрядную сетку далее 20-го кю. Тогда игра начинающего оценивается примерно 35-м кю. Отметим, что первая машинная программа Го сражалась в силу 30-го кю.

Забавно, что после проникновения Го на Запад первыми "жертвами" стали представители точных наук, которых игра привлекла простотой правил и вместе с тем их своеобразной математичностью. При более глубоком анализе обнаруживаются различные параллели между Го и такими разделами современной математики, как теория графов и распознавание образов. Не случайно игрой серьезно заинтересовались специалисты в области ЭВМ. Правда, успехи машин в Го пока не так велики, как в шахматах.

Описание игры. Для игры в Го надо иметь доску и набор камней двух цветов - белого и черного. Стандартная доска изображена на рис. 68 (она не раскрашивается). Игровое поле образовано пересечением 19 вертикальных и 19 горизонтальных прямых (при этом говорят о доске 19*19, хотя "по-шахматному" ее размеры 18*18). Прямые пересекаются в 361 точке, которые называют пунктами (как в рэндзю), на них-то и ставят камни.

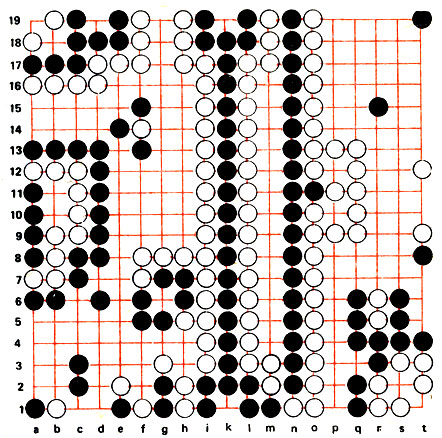
Рис. 68

Обычный комплект состоит из 180 камней каждого цвета, но практически достаточно иметь по 150 камней. Иногда применяют доски меньших размеров, так в выпускаемом у нас комплекте - доска 13*13 и 90 пар камней. Если у вас нет специального комплекта, то вместо камней можно взять белые и черные шашки, фишки или пуговицы двух цветов. Доску легко начертить на листе плотной бумаги или на картоне.

Как в реверси и рэндзю, начинают в Го черные. Игроки ходят по очереди, выставляя на один из свободных пунктов доски камень своего цвета. Поставленные камни не передвигаются, но могут попадать в плен. Го относится к "территориальным" играм, ее цель - захватить максимальное пространство на доске. Для этого игроки выстраивают на доске цепочки своих камней, из которых затем образуются группы.

Цепочка - произвольный набор связанных между собой камней одного цвета (соединяться они должны по линиям доски). Например, на рис. 68 прямая n вместе с камнем m1 образует цепочку из 19 черных камней, а на прямых от 1 до m возникла цепочка из 25 камней того же цвета.

Для каждого камня и цепочки существует понятие степени свободы. Число степеней свободы одного камня равно числу свободных пунктов, соседних с ним по вертикали и горизонтали. Число степеней свободы цепочки равно сумме степеней ее камней. В случае когда остается только одна степень свободы, говорят, что камень (или цепочка) находится в положении атари.

Далее будем правила сопровождать описанием некоторых игровых моментов. Рассмотрим пример на рис. 68. Черный камень t19 в вершине угла имеет две степени свободы: t18 и tl9, а белый камень t12 - три: t11, t13 и s12. Максимальное число степеней свободы одного камня равно четырем, как, например, у черного камня t15. Если белый и черный камни стоят на соседних пунктах, то число степеней у каждого из них уменьшается: оба забрали их , по одной друг у друга, примером служат камни t9 и t8.

Цепочка из двух черных камней с2, с3 имеет шесть степеней свободы, а цепочка белых r5, r6 находится в положении атари, у нее лишь один свободный пункт r7. Также одну степень свободы имеет цепочка g7, h6, h7. Рядом с ней находится еще одна цепочка из трех черных камней, но эти цепочки не соединены в одну, так как перейти по соседним камням с одной на другую нельзя.

Некоторые близко расположенные, но не связанные между собой цепочки могут быть надежно разделены камнями или цепочками противника. В этом случае говорят, что они отрезаны друг от друга. Так, на рис. 68 черная цепь на прямой n отрезана от черной цепи на прямой к. Сверху они не могут соединиться, так как белыми занят пункт m19, а снизу имеется диагональный разрез. Однако, разбив на части силы черных, белая цепочка отрезала от своих камней и саму себя.

Если какая-либо цепочка (или камень) полностью окружена камнями противника, то есть у нее не осталось ни одной степени свободы, то она считается взятой в плен и снимается с доски. Пленные камни становятся собственностью противника. На рис. 68 при расположении белого камня на d1 в плен попадает черный камень e1, находившийся в положении атари (на освободившийся пункт можно снова ставить камни). При ходе черных f2 плененным оказывается камень f1. Аналогично в плен захватываются две белые цепочки (по два камня каждая) при выставлении черных камней в пунктах h3 и r7, а при ходе белых g6 в плен попадают три черных камня.

Последний пример следует рассмотреть внимательнее. При расположении белого камня на g6 этот "десантник" не получает ни одной степени свободы. Такой ход разрешается делать лишь в том случае, если выставленный камень забирает последнюю степень свободы камней противника, то есть пленит их. Если же пленения не происходит - атакуемая цепочка не стоит в атари,- занимать полностью окруженный пункт нельзя. Так, черные не могут пойти t1 и s2. Заметим, что в нашем примере после снятия с доски плененных черных камней g7, h6, h7 белый камень g6 обретает свободу.

Цепочки и камни, над которыми нависла угроза пленения, можно спасать, добавляя к ним новые камни. Скажем, ход белых r7 выводит цепочку двух белых камней из состояния атари, поскольку образовавшаяся удлиненная цепочка имеет уже три степени свободы. Подобным образом ставя камень на g6, черные выручают три своих камня, присоединяя их к трем другим камням. В результате возникает цепочка, состоящая из семи черных камней с четырьмя степенями свободы,- окружить ее непросто.

Более важным объединением камней для игры является группа. Это одна или несколько цепочек, окружающих хотя бы один пункт доски. Пространство, окруженное группой, называется глазом. Группа может окружать и несколько глаз. Как мы сейчас убедимся, достаточным условием жизнеспособности группы служит наличие в ней не менее двух окруженных глаз. Степени свободы группы можно разделить на внутренние и внешние, ведь группа - это не просто "забор", а ограда, огораживающая определенное пространство.

Можно занимать камнями пункты, находящиеся как вне группы, так и внутри. Группа попадает в плен, если очередным ходом противник лишает ее всех степеней свободы. Но если у группы два глаза, то пленить ее практически невозможно. На рис. 68 большая черная группа с двумя глазами kl, kl9 полностью окружена снаружи. Но как окружить ее изнутри? Ход k1 невозможен, так как пленником окажется сам атакующий белый камень. По той же причине не удается пленить и белую группу с глазами s2 и t1.

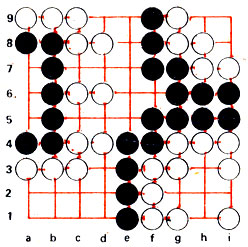
Рис. 69

Для групп с одним глазом нет общего правила нападения и защиты. Рассмотрим некоторые часто встречающиеся виды "одноглазых" групп, изображенных для простоты на доске 9*9 (рис. 69). На ее левом краю расположена черная группа с пятью степенями свободы, двумя - с5, с7 снаружи и тремя - а5, а6, а7 изнутри. Белые создали надежное окружение, прижав черные камни к краю доски. Наружные степени свободы легко ликвидировать, и судьба группы целиком зависит от внутреннего пространства. Белые могут пойти а6, после чего у черной группы останется два свободных пункта а5 и а7. Если черные сами займут один из них, то белые оккупировав предварительно пункты с5, с7, поставят свой камень на последний свободный пункт и возьмут в плен всю черную группу. Очевидно, черные не будут стремиться к самоуничтожению. В этом случае белые сами сделают ход на предпоследний внутренний свободный пункт. Черные займут последнюю общую степень свободы и возьмут в плен два белых камня. Но это лишь временное спасение черной группы. Глаз стал меньше - в нем осталось только два свободных пункта, скажем а5 и а6. На следующем этапе атаки белых произойдет высадка нового десанта в пункт а6. Снова у черной группы останется одна степень свободы. Черные пленят белый камень ходом а5, но это ничего не изменит, так как число степеней свободы не увеличится. Еще раз белые пойдут внутри группы и полностью снимут ее с доски, получив девять пленных черных камней и дополнительное свободное пространство. Эти приобретения, очевидно, полностью компенсируют потерю ими трех камней.

Мы привели столь подробное описание атаки группы камней, обладающей глазом, так как это часть базиса, на котором строится тактика Го. В данном примере ход черных аб гарантировал жизнь группе, хотя внутреннее пространство черных при этом уменьшилось. Пункты, подобные аб, называются критическими. В зависимости от очередности хода игроки, выставляя в них камни, либо образуют два глаза, либо, наоборот, лишают противника такой возможности.

На рис. 69 представлены две белые группы с единственными критическими пунктами - i9 и h2. Чей бы ход ни был, одна из этих групп гибнет, а другая спасается (при своем ходе черные, разумеется, захватят большую группу).

Если игроку не удается образовать группу с двумя глазами в одной цепочке, то он может попытаться объединить вместе несколько цепочек. Рассмотрим белую группу из шести камней, имеющую глаза в пунктах t1 и s2 (рис. 68). Две цепочки не соединяются между собой, но зато они надежно окружают два свободных пункта.

Особая ситуация, называемая ко, запрещает повторение позиции на доске. Приведем пример. На рис. 70 черный камень а9 может быть пленен ходом белых а8. Кажется, что теперь черные, в свою очередь, продолжая а9, могут взять белый камень а8. Однако по правилу ко этот ход запрещен, так как после него положение на доске полностью повторяется. Лишь при появлении какого-нибудь камня в другом месте доски черные смогут пойти а9.

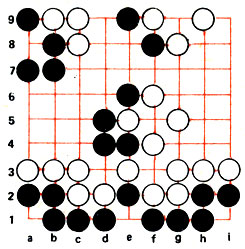
Рис. 70

На рис. 70 приведены основные разновидности ко-ситуаций: уже рассмотренное ко в углу, ко в центре доски и два варианта ко на краю доски. Внимательно взглянем на нижний край доски, где ко образуется после хода белых e1.В отличие от трех других случаев здесь решается судьба большой группы камней. Если пункт e1 займут черные, то они получат крепкую группу камней с глазами. Пусть сейчас ход белых. Играя e1, они снимают камень е2 и разделяют черных на две нежизнеспособные группы. По правилу ко черные не могут сразу ответить е2. Их задача - отвлечь противника на другом участке доски, после чего все-таки сыграть е2. Если же белые закрепятся на e1, у противника образуются две обреченные на гибель группы, имеющие по одному глазу. Подобная борьба за пункты называется ко-борьбой, а само правило ко используется как сильное тактическое средство. Еще раз с примером ко-борьбы мы встретимся ниже, рассматривая партию в Го.

Познакомимся еще с одной часто встречающейся ситуацией на доске. Ситуация сэки - это вынужденное, мирное существование цепочек противоположного цвета: атака со стороны одной из них кончается ее же гибелью. Степени свободы в зоне сэки являются нейтральными, они не принадлежат ни черным, ни белым. Две основные разновидности сэки показаны на рис. 68. В одном случае это взаимоокруженные цепи с двумя общими степенями свободы b10 и b11 на левом краю доски, в другом - у окруженных групп имеется по одному глазу и по одной общей степени свободы b18. Во втором случае ситуация представляет собой сэки, так как ходить на а19 и b19 равносильно самоубийству. И ход b18 тоже погубит того, кто его сделает, хотя он и не противоречит правилам игры. На рис. 68 показан еще один пример равновесия сил: две цепочки, у которых целая линия общих степеней свободы, от m4 до ml6. Занятие свободных пунктов линии m будет прекращено, как только останутся два последних пункта. Следовательно, все 13 незанятых пунктов являются нейтральными.

Как же завершается партия в Го? В ходе игры на доску ставятся один за другим белые и черные камни. Некоторые из них попадают в плен, другие образовывают активные группы. Наконец наступает момент, когда один из игроков видит, что его следующий ход не принесет ему новых приобретений (пленных камней или пунктов территории), а, наоборот, может лишь привести к потерям. В этом случае игрок пасует, то есть отказывается от своего очередного хода. После ответа противника он может снова ставить камни. Но если и второй игрок пасует сразу вслед за первым, то партия заканчивается, и партнеры переходят к подсчету очков. Конечно, опытные игроки пасуют только тогда, когда видят, что дальнейшая игра не даст принципиальных изменений на доске. Обычно это означает, что вся доска разделена на белую и черную территории.

Для подсчета очков сначала заполняют невыставленными камнями нейтральные пункты, граничащие как с белыми, так и с черными камнями (эти пункты не учитываются при подсчете). После этого на доске остаются пустыми только пункты, являющиеся глазами групп. За каждый такой пункт внутри глаз одного цвета игроку дается очко, очко приносит ему и один плененный камень. У кого сумма очков больше, тот и объявляется победителем. Чтобы отдельно не подсчитывать пустые пункты территории игроков и пленные камни, поступают так. Свободные пункты территории белых заполняются попавшими в плен белыми камнями, а на территорию черных соответственно выставляются черные камни, плененные белыми. В результате подсчет упрощается. Пример конкретного подсчета очков будет дан в приведенной ниже партии.

Статистика игры Го на доске 19*19 показывает, что если силы соперников примерно равны, то черные, начинающие партию, в среднем выигрывают с преимуществом пять очков. Поэтому по современным правилам игры белым при подсчете добавляется пять с половиной очков. А при игре с форой при равенстве очков выигрывает дававший фору. Таким образом, ничьих в Го не бывает.

Повторим кратко правила игры.

1. Начинают черные. Ходы делаются по очереди (пас тоже ход).
2. Не разрешается делать хода, приводящего к повторению позиции на доске (имеется в виду не только расположение камней, но и очередность хода). В подавляющем числе случаев это связано с ситуацией ко.
3. Камень (или группа камней) без степеней свободы снимается с доски при занятии последней степени свободы.
4. Не разрешается уничтожать последнюю степень свободы собственных камней, если при этом не берутся в плен камни противника.
5. Игра заканчивается после двух пасов, сделанных подряд.
6. Выигрывает получивший наибольшую территорию (после выставления плененных камней на территорию противника).

Для лучшего понимания правил и игровых моментов, которые мы затронули, рассмотрим несколько интересных задач (рис. 71), составленных игроком девятого дана (высшая ступень мастерства) японцем Маэда Нобуаки.

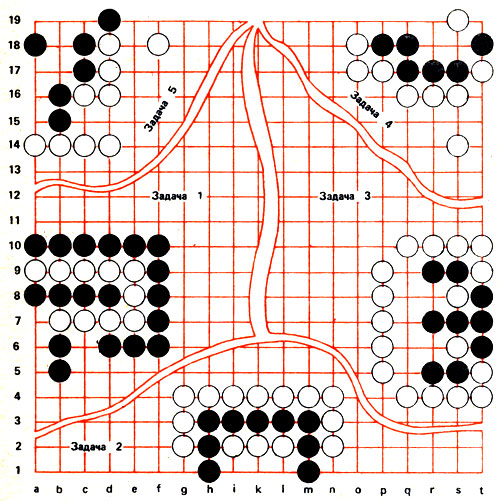
Рис. 71

Задача 1. Ход черных. Как захватить в плен белую цепочку, окружившую четыре черных камня?

Решение. 1. а7 2. а6 3. а7 4. а8 5. с8. Теперь группа белых камней не в состоянии образовать два глаза, так как пункт с8 критический, а пункт а7 не является глазом.

Задача 2. Ход черных. Как избежать пленения?

Решение. 1. к1! Единственный ход. Черные образовали сэки, и несмотря на то что внутри их группы находятся три белых камня, противник не может пожертвовать ими. Жертвенная цепочка окажется изогнутой, что позволит черным легко соорудить два глаза.

Задача 3. Ход белых. Как взять в плен все черные камни?

Решение. 1. q7 2. r8 3. r6 4. g6 5. r6. Черные не могут спастись, на 6. q5 решает 7. s6, а не 6. s6 - 7. g5. В данной задаче первый ход белых не единственный.

Задача 4. Ход черных. Как спасти группу?

Решение. 1. r19 2. s18 3. р19 4. t19 5. r18 6. t16 7. t18. Черные образовали два глаза - q19 и s18, s19, t19. Если бы белые на шестом ходу присоединили три своих камня к камню t17 ходом t18, то после 7, t16 противник взял бы в плен пять камней вместо трех.

Задача 5. Ход белых. Как взять в плен черную группу?

Решение. 1. b17 2. а17 3. а15 4. а16 5. b19! Если теперь черные играют 6. b18, то следует ответ 7. с19, и, жертвуя два камня b19, с19, белые ликвидируют один глаз черных. Если черные сразу перекроют выход из своей группы посредством с19, то белые ходом Ы8 объединяют три своих камня, и после их пленения ход b18 приведет к положению с одним критическим пунктом, как в задаче 1.

Партия двух неопытных игроков. На примере партии на учебной доске 9*9 мы поясним некоторые правила Го. Для записи партий удобно номера ходов показывать прямо на камнях. Поскольку нумерация сквозная, ходы черных всегда нечетные, а ходы белых - четные (кроме игры с форой, когда начинают белые). Если ход следует на пункт, уже занимавшийся камнем, оба номера пишутся рядом под диаграммой.

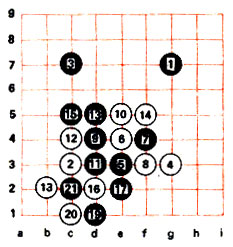
Рис. 72

Ходы 1-21 показаны на рис. 72. Первые четыре камня поставлены игроками в разных углах доски. Действительно, захватить территорию в зоне угла легче - помогают края доски. После пятого хода возникают осложнения. Ходом е3 черные вторгаются в потенциальные владения белых, чтобы помешать противнику окружить нижнюю часть доски. Белые используют активную защиту, "накрывая" черный камень ходом 6. Ходами 7 и 9 черные не возражают против такого развития событий, надеясь получить богатые возможности по отгораживанию центра доски. Однако ходом 10 белые не отдают камень 6. Черные вынуждены соединить в цепочку свои камни ходом 11. Теперь белые должны защищать левый нижний угол от превосходящих сил черных (цепочка 9, 11, 5). Белые начинают строить цепочку ходом 12, тем самым пытаясь защитить левый нижний угол. Черные удлиняют цепочку ходом 13, преследуя три цели: оказаться поближе к угловому камню 3, выйти на левый фланг, если белые ответят справа, и выйти на правый, если белые ответят слева. Белые стабилизируют правый фланг. В результате камень 7 попадает в атари. Ходом 15 черные выходят на левый фланг. Положение белых становится опасным, и ближайшими ходами они пытаются расположить камни так, чтобы получить действующую группу. Пока им это не удается, а после хода 21 возникает ко-угроза, и положение группы теперь зависит от того, кто возьмет верх в ко-борьбе.

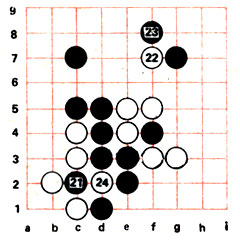
Рис. 73

Ходы 21-24 (рис. 73). По правилу ко белые не могут ходом 22 взять в плен камень 21, мешающий образованию глаз, и ходом 22 создают ко-угрозу, нападая на угловой камень черных. Ходом 23 .черные защищают угол, белые в ответ берут в плен камень 21.

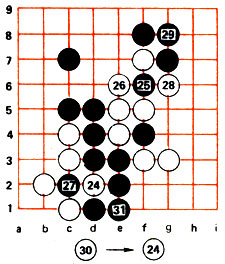
Рис. 74

Ходы 24-31 (рис. 74). После создания ко-угрозы ходом 25 белый камень f7 оказывается в положении атари. И все же этот ход неудачен, черным лучше было создать ко-угрозу ходом g4 с целью сыграть g5 и захватить верхнюю половину доски. Белые удлиняют цепочку е4, е5, f5 ходом 26, и черные оказываются в опасности. Чтобы не беспокоиться за верхнюю часть доски, им лучше было ходом 27 пойти е7, забирая в плен камень белых. Но они увлеклись ко-борьбой и берут нижний камень. Белые пользуются этим - после взятия в плен черного камня f6 ходом 28 они создают крепкую группировку на правом фланге. К тому же оказывается, что два черных камня в правом верхнем углу не выполняют своей защитной функции и нуждаются в подкреплении. Ходом 29 черные пытаются исправить положение. Белые берут в плен камень 27 (ходом 30 на место 24), а черные, на сей раз не имея сильной ко-угрозы, защищаются ходом 31.

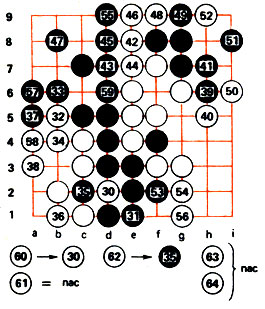
Рис. 75

Ходы 32-64 (рис. 75). Используя неточность черных, белые пытаются стабилизировать свою угловую группу ходом 32. Ход 33 преграждает продвижение белых вверх и создает опасность отсечения белого камня b5. Белые реагируют ходом 34. Теперь черные стараются помешать формированию глаз посредством ко-угрозы. Белые защищают камень c1 ходом 36, что является грубой ошибкой. В этот ответственный момент им необходимо было пойти 36. а3. Тбгда белая группа сохранила бы шансы выжить, выиграв ко-борьбу в левом нижнем углу (например: 36. а3 37. b1 38. а5 39. а2 40. a1, или 37. а5 38. b1, и группа удерживается без ко-борьбы). Теперь черные могли взять в плен белую группу в углу, но не обнаружили комбинации. Ход 37 сокращает глаза группы, не уничтожая ее. Нужно было поставить камень в пункт а3. Белые сами занимают этот критический пункт и выживают.

Черным становится ясно, что белая группа выдержала натиск, и ходом 39 они приступают к образованию своей группы в противоположном углу доски. Однако ход этот слишком пассивен, приводит к потере инициативы. Белые легко ограничивают распространение черных вниз и делают важный ход 42, который атакует одновременно две черные группы, пока не имеющие глаз. Черные укрепляют верхний левый угол, но ход 46 не дает им возможности соединиться в правом углу. Ход 47 из разряда панических, лучше было получить глаз, продолжая d6. С другой стороны, и ход 46 неточен - логичней было включить обмен ходами: белые d6 - черные с6. После хода 48 группа черных обречена, хотя они и пробуют защититься ходом 51. Но ходом 52 белые занимают второй критический пункт h9.

Смирившись с потерями, черные пытаются сместить возможную границу в оставшиеся части доски ходом 53, но у них был гораздо более эффективный ход для уменьшения территории белых в данном месте, а именно h2! Белые не в состоянии отразить этот черный камень, и территория белых в углу сильно уменьшается. Вместо хода 55 лучше было gl (55. g1 56. h1 57. f1 58. h2). Ходом 56 белые, а вслед за ними и черные ошибочно отказались от d6. На ход 57 белые, конечно, отвечают а4. Наконец-то сделан ход 59. d6. Ходом 60 (на место 30) белые берут в плен камень 35. Черные пасуют, полагая, что никакой их ход не улучшит положения, хотя 61. g5 позволяло в ко-борьбе отвоевать одно очко. Белые закрывают ко ходом 62. Границы сформированы, игра закончена. Осталось привести доску к удобному для подсчета очков виду и подсчитать их.

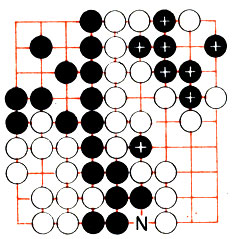
Рис. 76

На рис. 76 представлена доска после того, как сделан последний ход. Буквой N помечен нейтральный пункт, он никому не принадлежит, поэтому его можно заполнить любым камнем. Камни, помеченные плюсом, обречены на пленение - их разрешается снять с доски и присоединить к другим пленным камням.

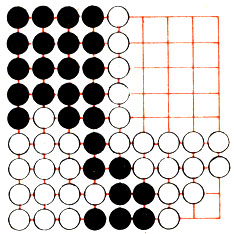
Рис. 77

Подведем итоги партии в Го (рис. 77). Черные взяли в плен три белых камня, а белые - четыре черных. Еще восемь черных камней обречены (они помечены плюсом), то есть соотношение пленных 12:3 в пользу белых. Черные выставляют пленников на территорию белых, а белые - на территорию черных. У белых осталось еще четыре пленных камня, которых территория черных не смогла вместить. Итак, территория белых состоит из 23 пунктов, у черных же вообще нет завоеваний. У белых имеется также четыре пленных камня, и даже без учета 5,5 очков они победили с преимуществом 27 очков.