n в ряд

В качестве обобщения крестиков-ноликов интересно проанализировать игры "n в ряд" на неограниченной плоскости при различных значениях п. Очевидно, по-прежнему побеждает тот, кто первым выстраивает п своих знаков в ряд. Как мы знаем, при n = 5 победа (теоретически) за начинающей стороной, то есть крестиками. Совсем легко выигрывают они при любом n<5. А что можно сказать об игре "я в ряд" при n>5?

Еще в 1954 году Г. Поллаком и К. Шенноном, одним из основоположников кибернетики, было доказано, что при n≥9 у второго игрока имеется беспроигрышная стратегия. В дальнейшем несколькими математиками был построен очень простой и эффектный ничейный алгоритм игры. Всю бесконечную доску надо мысленно разделить на квадраты 8*8 и заполнить их линиями, как показано на рис. 64. Теперь какую бы клетку ни занял первый игрок, второму необходимо пойти на клетку, лежащую на другом конце линии.

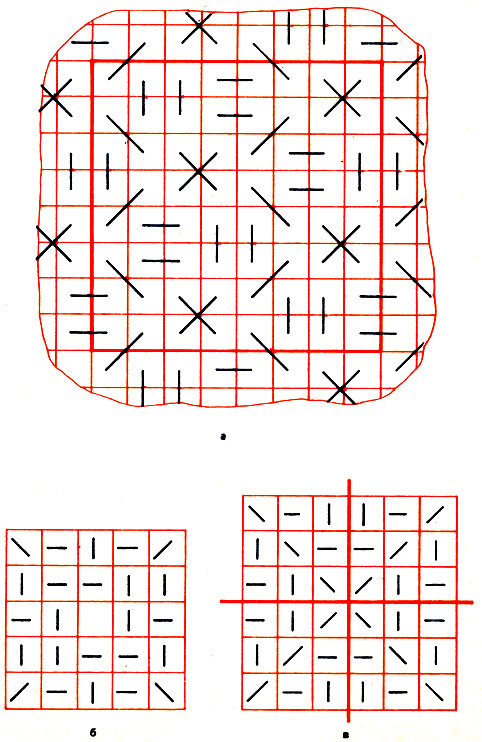
Рис. 64

Покажем, что такой способ игры гарантирует ничью. Рассмотрим для этого произвольный ряд из девяти соседних клеток бесконечной плоскости. Наш квадрат обладает тем свойством, что среди этих девяти клеток обязательно найдутся две, связанные между собой линией. Это значит, что если одна клетка данной пары занята крестиком, то на другой обязательно стоит нолик. Таким образом, девять выбранных клеток не могут быть заполнены одними и теми же знаками, то есть начинающая сторона никогда не построит их девять в ряд (а тем более больше девяти), даже если игра будет продолжаться бесконечно.

Читатель, наверное, обратил внимание, что мы снова успешно применили парную стратегию, которая уже приводила нас к цели в таких играх, как бридж-ит и уголки. На сей раз такая стратегия оказалась успешной на бесконечной доске.

Впервые квадрат на рис. 64 придумали американские математики А. Хэйлс и Р. Джуитт. Любопытно, что ленинградцы А. Давлицаров и О. Степанов нашли подобный квадрат при помощи ЭВМ.

К сожалению, рассмотренная стратегия, отличающаяся своим изяществом, не пригодна для значений n≤8. Однако доказано (более сложным способом), что игра "8 в ряд" на неограниченной доске также ничейна. Что же касается вопроса о результате игр "7 в ряд" и "6 в ряд", то он пока остается открытым. Впрочем, А. Давлицаров и О. Степанов доказали ничейность придуманных ими "экваториальных" крестиков-ноликов "7 в ряд": на плоскости выбрано определенное направление - это и есть экватор, параллельно которому выстроенные в ряд семь одинаковых знаков не считаются за выигрыш.

В завершение вернемся к игре "5 в ряд", но на доске ограниченных размеров - 5*5. В этом варианте нолики совсем легко добивается ничьей. Им вновь следует воспользоваться методом Хэйлса и Джуитта. После каждого хода крестиков в любой из помеченных на рис. 64 б квадратов нолик следует ставить в квадрат с такой же пометкой и в направлении, указанном ею самой. При этом нолики могут даже дать фору партнеру, разрешив в начале игры занять центральный квадрат и сделать еще один ход куда угодно. В конце игры в каждом возможном ряду из пяти клеток будет стоять хотя бы один нолик.

Аналогично достигается ничья и в игре "6 в ряд" на доске 6*6. Рис. 64,в похож на рис. 64,б, за исключением того, что ответный ход ноликов по диагонали может быть любым. "Покрытие" Хэйлса и Джуитта в данном случае отличается зеркальной симметрией по двум выделенным линиям.