Четыре и пять в ряд

Значительно глубже и интереснее такие игры в крестики-нолики, в которых победу приносят не три знака, поставленные в ряд, а четыре или пять. В игре "4 в ряд" на доске 4*4 ноликам сделать ничью еще проще, чем в классическом варианте 3*3. Для доски 5*5 эта игра была запрограммирована на ЭВМ. Машина действовала безукоризненно: ничьей достигала любым цветом, а при невнимательной игре человека одерживала победу. Кстати, доказано, что и на доске 5X5 данная игра ничейна.

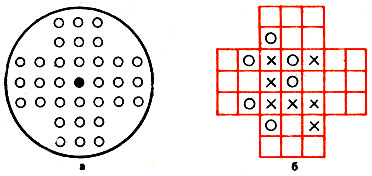
Рис. 63

В "4 в ряд" играют и на доске для солитера, изображенной на рис. 63 а. Она состоит из 33 полей с отверстием в каждом из них. Фишками служат колышки, которые вставляются в отверстия. Основной вариант солитера, популярный в прошлом веке, заключается в следующем. На всех полях доски расставляются фишки одного цвета, и одна из них вынимается (свободное поле). Ход представляет собой прыжок произвольной фишки по вертикали или горизонтали через соседнюю фишку, которая при этом - в отличие от уголков - снимается с доски. Как и в уголках, за один ход фишка может сделать несколько прыжков, и все фишки, через которые она перепрыгнула, удаляются.

Если ходов больше нет, партия заканчивается. Цель игры в том, чтобы на доске осталась всего одна фишка. Доказано, что, какую бы фишку ни убрали с доски, задание выполнимо, причем самое короткое решение содержит 15 ходов.

Классический солитер (ему посвящена обширная литература), по существу, является головоломкой. Однако у нас выпускается комплект игры (почему-то под новым названием - йога) в несколько расширенном виде. Учитывая, что люди охотнее играют в игры, чем решают головоломки, в нем предусмотрены также три игры. Для этого фишки-колышки окрашены с двух концов в два цвета (как в реверси), и каждый из партнеров играет своим цветом. Первая игра - обычные уголки. Игроки расставляют по шесть своих фишек в двух противоположных прямоугольниках 3*3 и по правилам уголков (допускаются и ходы по диагонали) стремятся занять неприятельскую территорию.

В другой игре, как и в традиционном солитере, на доске расставляются 32 фишки одного цвета, причем им разрешается перепрыгивать через любое количество фишек, примыкающих друг к другу, и все они снимаются с доски (приземляться надо сразу вслед за ними). Соперники ходят по очереди, побеждает тот, кто в конце игры соберет больший урожай фишек.

И наконец, третья игра, благодаря которой мы и вспомнили о солитере,- "4 в ряд". Вместо крестиков и ноликов в ней используются фишки двух цветов.

На рис. 63 б крестики соорудили вилку и выигрывают следующим ходом, ставя свой знак на одно из помеченных полей. Однако при правильной игре в крестики-нолики на доске для солитера результат ничейный.

Игра квадрат (другое название "тико") представляет собой сочетание "4 в ряд" и болотуду. Ведется она на доске 5*5, у каждого игрока по 4 шашки. Цель игры - выстроить шашки своего цвета вдоль одной линии или в виде квадрата 2*2. Прежде всего партнеры по очереди расставляют шашки (счетверять их запрещается), после чего перемещают их на любые соседние поля (по вертикали, горизонтали или диагонали).

Игра "4 в ряд" на кубической доске 4X4X4 называется тик-так-тоу. Долгое время считалось, что она ничейна, но недавно компьютер установил, что у начинающего игрока имеется стратегия, обеспечивающая ему победу.

Теперь, наконец, настала очередь самой популярной игры в крестики-нолики. На неограниченном поле (листе клетчатой бумаги) двое, один за другим, ставят свои знаки. Выигрывает тот, кто раньше выстроит пять знаков в ряд (по вертикали, горизонтали или диагонали). Если никому не удается это сделать, игра завершается вничью. Конечно, должны быть оговорены условия, сколько ходов может продолжаться партия.

Хотя теоретически игра ведется на безграничной плоскости, реально доска имеет конечные размеры, обычно это просто лист клетчатой бумаги. Имея под рукой карандаш и бумагу, в игру "5 в ряд" охотно играют школьники, студенты и даже кандидаты и доктора наук, а придумана она была четыре тысячи лет назад, задолго до того, как появились тетради в клетку... Кстати, старинные игры гобанк и гомоку отличаются от крестиков-ноликов "5 в ряд" только наличием специальных досок 19*19 (как в Го) или 15X15, а вместо значков используются фишки.

В большинстве игр, рассмотренных в данной главе, нолики борются за ничью. Имеется в виду, что крестики (начинающая сторона) всегда могут ее достичь. Это интуитивное соображение подтверждается следующей теоремой.

При правильной игре в крестики-нолики "5 в ряд" или вообще "п в ряд" при любом п начинающему партию гарантирована ничья.

Докажем это от противного. Предположим, что, как бы крестики ни играли, нолики, применяя наилучшую стратегию, побеждают. Тогда начинающий, поставив свой первый крестик на любое поле, далее должен воспользоваться стратегией партнера, мысленно поменяв знаки - крестики и нолики. Если на каком-то ходу согласно этой стратегии ему надо занять поле, где стоит самый первый крестик, он вновь ставит знак на любое поле доски и т. д. Ясно, что лишний знак крестиком никогда не помешает. По нашему предположению, нолики должны выиграть. Однако стратегия крестиков такова, что они как бы играют ноликами, да еще с лишним знаком, значит, тоже выигрывают. Мы пришли к противоречию, что и доказывает теорему.

Приведенное доказательство почти такое же, как и в шахматной игре "два хода подряд". Как видите, мы здесь снова воспользовались идеями симметрии. Кстати, теорема справедлива как для бесконечного поля, так и для досок заданного размера.

Хотя у нас встречались игры, в которых побеждает вторая сторона, обычно право первого хода дает определенное преимущество. При этом в шахматах и шашках оно не слишком велико, а в крестика-ноликах в вариантах "3 в ряд" и "4 в ряд" является решающим (в первом случае при добавлении одного поля к доске 3*3, во втором - на доске размером 6*6 и больше). А какова ситуация в игре "5 в ряд", существует ли форсированный выигрыш у начинающего игрока? Практика показывает, что заметная инициатива принадлежит крестикам, но нередко и нолики берут верх. Но как утверждают знатоки рэндзю (об этой модификации крестиков-ноликов речь пойдет в следующем разделе), в японских книгах приводятся исчерпывающие варианты, как выиграть, начиная игру. К своему десятому ходу крестики получают решающий перевес, а к пятнадцатому завершают построение пятерки.

Хотя эти теоретические рассуждения вряд ли напугают любителей крестиков-ноликов, все же говорить о серьезных состязаниях, если доказан выигрыш одной из сторон, не приходится. Поэтому и были придуманы некоторые дополнения, при которых результат игры становится не столь определенным. Но прежде чем рассказать о шашках рэндзю, рассмотрим еще две модификации "шашечных" крестиков-ноликов. Вот игра, в которой засчитывается любое число шашек, стоящих подряд. На шахматной доске (можно взять и доску меньших размеров) двое по очереди ставят по две шашки своего цвета, стремясь выстроить из них горизонтальные или вертикальные ряды как можно большей длины. Ряд из двух одноцветных шашек дает их владельцу 4 очка, из трех - 9 очков, из четырех - 16 очков и т. д. (конечно, можно ввести и другие оценки). Шашка, стоящая одновременно в двух рядах, учитывается только 1 раз. После того как будет заполнена вся доска, ведется подсчет очков. У кого окажется больше, тот и выиграл.

Игра хасами шоги содержит элементы сразу нескольких игр - крестиков-ноликов, уголков и простых шашек. Игра ведется на доске 9*9. У каждого из партнеров по 18 шашек, занимающих две крайние горизонтали (белые с одной стороны, черные с противоположной). Цель игры - выставить первым пять своих шашек в ряд по любой линии в пределах пяти средних рядов. Шашки могут ходить по вертикали или горизонтали на одно поле или перепрыгивать через соседнюю шашку, занимая свободное за ней поле. Если один из играющих зажмет неприятельскую шашку (по вертикали, горизонтали или диагонали) между двумя своими, то она снимается с доски; в то же время шашка может безопасно проходить между двумя шашками противника. В продаже имеется упрощенный вариант игры. Доска 8X8, у соперников по 16 шашек, и выигрывает тот, кто выстраивает не пять, а четыре шашки в ряд.