Уголки

Начнем с классического варианта уголков, знакомого каждому. В углах доски 8X8 расположено по десять белых и черных шашек (рис. 49). Противники ходят по очереди, причем ходы могут быть двух типов: 1) перемещение шашки на соседнее свободное поле по вертикали или горизонтали (но не по диагонали!); 2) последовательное перепрыгивание шашки через свои или чужие по свободным полям вдоль вертикалей или горизонталей доски (каждый скачок в процессе такого хода может производиться только через одну шашку с "приземлением" на поле, следующее сразу за ней).

Рис. 49

Выигрывает тот, кто раньше занимает своими шашками противоположный угол доски, то есть исходные поля шашек противника. Впрочем, если белые уже заняли своими шашками необходимый угол, это еще не "мат". Если следующим ходом и черные занимают противоположный угол, то партия признается ничейной (партнеры сделали равное число ходов).

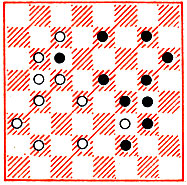
Рис. 50

Рассмотрим позицию на рис. 50. Шашка b5 может пойти на поле а5 - ход первого типа; на поля b7, d5, d7, f5, f7, h5, h7 - ходы второго типа. Заметим, что один и тот же ход может быть иногда сделан разными способами, в нашем примере шашка b5 может попасть на поле h7 по двум траекториям: b5-b7-d7-f7-h7 или b5-d5-f5-h5-h7.

Если игрок не двигает с первоначального места одну или несколько своих шашек, то, очевидно, противник никогда не сможет добиться цели, и игра теряет смысл. Поэтому в уголках вводится правило, по которому через определенное число ходов, например 40, оба партнера должны полностью освободить от шашек свой угол.

Кажется, что после введения последнего правила игра становится очень увлекательной. Однако это не совсем так. Как мы увидим, черные могут без всякого труда добиться ничьей, и, значит, игра заметно теряет спортивный интерес.

Собственно, дело происходило так. Коллега автора книги, известный математик Д. Поляк, долгое время наблюдал, как его дочь-восьмиклассница "резалась" со своими подругами в уголки. Наконец, это праздное времяпрепровождение стало огорчать отца (уж лучше бы сражались в шахматы, подумал он). Вот тогда-то он и придумал ничейный алгоритм игры за черных. Надо сказать, что девочки были несколько разочарованы, но играть в уголки перестали и переключились на более интеллектуальные занятия.

Сейчас мы снова воспользуемся идеями симметрии, которым было уделено много внимания в предыдущей главе. Алгоритм игры черных в уголки прост - на каждый ход белых им достаточно отвечать ходом, симметричным ему относительно центра доски - точки О на рис. 50.

Воспользуемся для удобства числовой системой координат - поле (i, j) лежит на пересечении i-й вертикали и j-й горизонтали. Очевидно, для поля (i, j) центрально-симметричным является поле (9-i,9-j). Поэтому, если белые ходят шашкой с поля (i, j) на поле (k, l), то черные должны ответить ходом с (9-i, 9-j) на (9-k, 9-l). Например, на рис. 50 на ход белых b6-d6 черные играют g3-e3.

При описанной стратегии черных после каждого их хода центрально-симметричное расположение шашек на доске сохраняется, и в тот момент, когда белые займут своими шашками противоположный угол доски, черные ответным ходом также займут угол, и партия закончится вничью.

Разумеется, еще надо доказать, что на любой ход белых возможен симметричный ответ черных. Рассмотрим симметричную позицию, в которой каждой белой шашке соответствует симметричная черная, и наоборот. Отсюда следует, что всякому незанятому полю будет симметрично также незанятое.

Очевидно, при центральной симметрии вертикали (горизонтали) с номером i соответствует вертикаль (горизонталь) с номером 9-i, а соседние по вертикали (горизонтали) поля переходят в поля, также соседние по вертикали (горизонтали).

Пусть при своем ходе белая шашка передвинулась на соседнее незанятое поле. Ему симметрично незанятое поле, соседнее с черной шашкой, которая была симметрична белой до ее хода. Поэтому следующим ходом эта черная шашка также может пойти на данное незанятое поле.

Пусть теперь белая шашка делает ход типа скачка. Назовем занятые поля, через которые она перепрыгивает, опорными. Рассмотрим позицию на доске до этого хода белой шашки. Симметричная ей черная шашка в этот момент имела возможность перемещаться по симметричной траектории, поскольку опорным полям соответствуют опорные, свободным - свободные, и "соседство" между ними сохраняется. Докажем, что этот ход черных возможен и после хода белых. Ход белой шашки мог бы помешать симметричному ходу черных в одном из двух случаев: 1) после своего хода белая шашка заняла свободное поле на траектории черной; 2) до своего хода белая шашка была опорной в траектории черной шашки. Покажем, что оба эти случая невозможны.

Пусть белая шашка имеет координаты (i, j), тогда координаты симметричной черной (9-i, 9-j). При каждом прыжке шашки через опорное поле четность ее координат сохраняется, то есть координаты всех свободных полей траектории имеют ту же четность, что и координаты исходного поля. Но если число i четно, то число 9-i нечетно, и наоборот. Поэтому белая шашка после своего хода не может попасть на свободное поле траектории черных. Далее, одна из координат опорного поля совпадает с координатой соседнего с ним свободного поля траектории и, следовательно, имеет ту же четность, что и соответствующая координата исходного поля. Но числа каждой пары (i, 9-i) и (j, 9-j) имеют разную четность, и поэтому поле (i, j) не может быть опорным для шашки (9-i, 9-j).

Итак, оба случая опровергнуты, и после хода белых симметричный ход черных возможен. Поскольку начальная позиция центрально симметрична и таковой остается после каждого ответного хода черных, то их ничейная стратегия торжествует!

Любопытно, что рассмотренная нами "теория" уголков оказывается неверна, если допустить диагональные прыжки шашек. В этом случае белая шашка до своего хода могла быть опорной в траектории симметричной черной шашки. Так, на рис. 50 после хода белых d4-f6 черные не в состоянии скопировать ход противника.

Мы предполагали до сих пор, что игра протекает на обычной доске 8*8. Те же рассуждения справедливы и для любой доски с четными сторонами и произвольной центрально-симметричной начальной позицией. Однако метод игры, гарантирующий черным ничью, уже не годится для доски, у которой хотя бы одна сторона нечетна.

Итак, черные, играя в обычные уголки, легко делают ничью. Однако, как ни странно, трудно доказать, что ничья в этой "скучной" игре гарантирована и белым. Думаем, что эта задача не из простых. Так, в простейшем варианте уголков с одной белой шашкой на поле a1 и одной черной на поле h8 у белых имеется всего два способа сделать ничью - их шашка должна идти по первой горизонтали с a1 до h1 и далее по крайней вертикали с h1 до h8 либо должна перемещаться по вертикали с a1 до а8 и затем по горизонтали с а8 до h8. В обоих случаях дело заканчивается ничьей на 14-м ходу, а любое отступление шашки белых от края доски, как нетрудно убедиться, приводит их к проигрышу.

Хотя мы и раскритиковали игру в уголки, но сами же указали, что на досках определенных размеров возможна полноценная борьба, и алгоритм ничьей, а тем более победы, не известен. Кстати говоря, в магазинах игрушек продаются различные игры ("в четыре угла", "лабиринт", "по местам"), напоминающие собой уголки. Игра в них ведется на необычных досках, правила перемещения фишек различны, но цель всюду одна - оккупировать своими фишками территорию противника, и кто раньше это сделает, тот и побеждает.

Основная особенность игр типа уголков заключается в том, что белые и черные шашки (фишки) меняются местами. Поэтому такие игры можно назвать перестановочными. Известно много перестановочных игр и развлечений, самая знаменитая из которых - игра в "пятнадцать", придуманная С. Лойдом. Это не настоящая игра, а головоломка (соперников здесь нет) и к нашей книге непосредственного отношения не имеет, но она слишком знаменита, чтобы не уделить ей несколько строк.

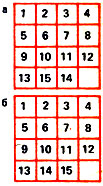
Рис. 51

В коробочке размером 4*4 находится пятнадцать квадратов, занумерованных числами от 1 до 15 (одно из возможных расположений показано на рис. 51а). Требуется, не вынимая квадратов, переставить их так, чтобы номера шли в возрастающем порядке (рис. 51б).

За решение головоломки в начальной "позиции" на рис. 51а Лойд назначил большую денежную премию. Правда, он ничем не рисковал, так как предварительно доказал, что задание невыполнимо. Всего существует 16! различных расположений квадратов, и все они распадаются на два равных по численности класса. Расположения одного класса приводятся при помощи перестановок к искомому виду (см. рис. 51 б), а расположения второго удается привести лишь к положению на рис. 51а, то есть с переставленными квадратами 14 и 15.

Как определить, к какому из двух классов принадлежит данное положение квадратов? Для этого нужно подсчитать число транспозиций в нем. Говорят, что два квадрата образуют транспозицию, если квадрат с большим номером предшествует квадрату с меньшим. Если число транспозиций четно, то позиция относится к первому классу (на рис. 51 б оно равно нулю), а если нечетно, то ко второму классу (на рис. 51а - одна транспозиция). Подробный анализ игры можно найти во многих книгах по занимательной математике.

Приведем еще одну старинную головоломку, в которой приходится менять местами фигуры разного цвета. Для этого снова вернемся к шахматам.

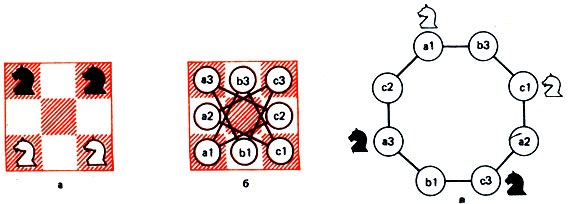
Рис. 52

В углах шахматной доски 3*3 стоят два белых и два черных коня (рис. 52а). Поменять местами белых и черных коней за минимальное число ходов.

Эта задача, придуманная итальянцем Гуарини еще в XVI веке, хорошо знакома любителям занимательной математики. Она изящно решается при помощи "метода пуговиц и нитей", предложенного известным английским мастером головоломок Г. Дьюдени.

На каждое поле нашей маленькой доски, кроме центрального (на него кони не могут попасть), поместим по пуговице (на рис. 52 б их заменяют кружки). Если между двумя полями возможен ход конем, то лежащие в них пуговицы свяжем нитью (на рисунке нитям соответствуют отрезки, соединяющие кружки). Полученный клубок пуговиц и нитей распутаем так, чтобы все пуговицы расположились по кругу (рис. 52,в).

Теперь решение задачи находится почти автоматически. Выбрав одно из направлений по кругу, будем переставлять по нему коней до тех пор, пока они не поменяются местами. Необходимое перемещение коней по доске получается заменой пуговицы соответствующими полями. Нетрудно убедиться, что решение состоит из 16 перемещений коней (восьми белых и восьми черных), причем кони разного цвета могут, ходить по очереди. Если поставить дополнительное условие, чтобы белые и черные кони при своем движении не угрожали друг другу (очередность ходов в этом случае можно нарушать), то решение также находится из распутанного клубка. Нужно следить лишь за тем, чтобы кони разного цвета не оказались в этом клубке соседями. Если круговое движение (по часовой стрелке) начинает белый конь a1, то решение будет такое: Ka1-b3, Ка3-с2, Кс3-b1-а3, Кс1-а2-с3, Кb3-b1-а2, Кс2-а1-b3, Ка3-с2-а1, Кс3-b1-а3, Ка2-с3, Кb3-с1.

Метод пуговиц и нитей легко интерпретировать в терминах теории графов. Действительно, нашей задаче о перестановке коней можно сопоставить граф, вершины которого соответствуют полям доски (пуговицам), а ребра - возможным ходам коня (нитям). При этом распутывание клубка пуговиц и нитей, по существу, означает лишь более наглядное расположение построенного графа. Разумеется, метод пуговиц и нитей может быть использован не только в задаче Гуарини, но и для решения целого класса перестановочных задач, игр и головоломок (не обязательно шахматных).

Перестановочные головоломки возникают и в классических уголках, с которых мы начали этот раздел. Вот некоторые задачи, придуманные Ф. Бартеневым.

За наименьшее число ходов переставить по правилам уголков четыре шашки из левого нижнего угла доски - полей a1, a2, b1, b2 в правый верхний.

Решение состоит из 13 ходов: 1. а2-с2 2. a1-c1-с3. 3. b1-b3-d3 4. b2-d2-d4 5. c2-c4-e4. 6. c3-e3-e5 7.d3-d5-f5 8. d4-f4-f6 9. e4-e6-g6 10. e5-g5-g7 11. f5-f7-h7 12. f6-h6-h8 13. g6-g8.

Четыре шашки, расположенные в центре (на полях d4, e4, d5, e5), могут разойтись по четырем углам доски за 22 хода. Три шашки за 19 ходов могут дойти с полей a1, b1, c1 до f6, g6, пб и за 20 ходов с полей a1, a2, b1 до g8, h7, h8.

В обычных уголках шашки ходят по вертикалям и горизонталям доски 8*8, попадая то на белые поля, то на черные. Однако можно играть в уголки и по нормальным шашечным правилам, то есть в начале игры, как обычно, располагать шашки двух цветов на черных полях трех крайних горизонталей (по 12 с каждой стороны), а ходить по диагонали - на соседние поля или перескакивая через свои и чужие шашки. Победителем вновь становится игрок, который первым занимает своими шашками территорию противника.

Эта игра представляет собой одну из разновидностей "халмы", в которой используются самые разнообразные доски. Поскольку в данном варианте игры ходы совершаются по диагонали, то ничейный алгоритм не работает, хотя исходное положение шашек является центрально-симметричным.

Другая игра, представляющая собой смесь шашек и поддавков, известна под названием "сальто". Считается, что эта игра придумана участниками международного шахматного турнира, состоявшегося в 1900 году в Монте-Карло. Правда, играют в нее на доске 10Х 10, причем шашки (по 15 с каждой стороны, в начале игры они расположены на трех крайних горизонталях доски) имеют отличительные символы, изображающие звезду, луну и солнце. Игра, пожалуй, слишком искусственна, и мы не станем описывать ее в деталях.

В заключение этого раздела приведем одно "упражнение" для халмы на доске 8X8. Требуется переставить 12 белых шашек со своей территории на пустую территорию противника как можно быстрее.

Цели удается добиться за 20 ходов: 1. а3-b4 2. c1-a3-c5 3. b2-d4-b6 4. a1-b2 5. b2-d4 6. с3-а5-с7 7. b4-d6-b8 8. e1-c3-e5 9. d2-f4-d6 10. h2-f4 11. c5-a7 12. e3-c5-e7 13. d4-f6-d8 14. g1-e3-g5 15. f2-h4-f6 16. e5-g7 17. g7-h8 18. g3-e5-g7 19. f4-h6-f8 20. g5-h6.

Сократить это решение, по-видимому, невозможно, хотя и доказать это не так легко. Известно лишь простое доказательство того, что задачу нельзя решить меньше чем за 16 ходов. Приведем его. В начальном положении восемь шашек занимают нечетные горизонтали - первую и третью, а четыре шашки стоят на второй, четной горизонтали. В заключительном положении восемь шашек находятся на двух четных горизонталях, шестой и восьмой, а четыре - на нечетной, седьмой. Итак, четыре шашки изменили четность своих горизонталей. Чтобы добраться до места назначения, каждая из этих шашек должна хотя бы раз перейти на соседнее поле (чтобы изменить четность) и хотя бы раз Прыгнуть через другие шашки ( чтобы перебраться в лагерь противника). Остальные восемь шашек делают хотя бы по одному ходу. Итого 4*2 + 8*1 = 16.