Поддавки

Правила игры простые и знакомы каждому. Выигрывает тот, кто первым отдаст все свои шашки либо останется только с запертыми. У поддавков весьма богатая история. Игрой занимался еще первый русский теоретик шашек и шахматный мастер А. Петров, который писал, что она требует большего расчета, чем обычные шашки. В настоящее время у игры много любителей, в Москве в 1978 году был даже организован всесоюзный клуб "Шашечница", где проводятся соревнования по поддавкам, изучается теория. В данном разделе содержится, в частности, ряд идей и находок, принадлежащих членам этого клуба.

В "Толковом словаре" Вл. Даля о поддавках сказано, что это игра в шашки, где "проигравший считается выигравшим". Определение точное, оно удачно подчеркивает "односущность" поддавков и обычных шашек - правила в этих играх одни и те же, и можно сказать, что они совпадают с точностью до результата. А вот иная формулировка: поддавки - это обычная игра, только партнеры ходят шашками противника.

Классическая игра имеет разные названия: крепки, крепкие или простые шашки. Поддавки называют также обратными шашками, так как они получаются из простых путем обращения: понятия "выигрыш" и "проигрыш" меняются местами. Обращение симметрично, ведь обращенные поддавки есть крепкие.

Формально обратить можно любую игру, но в действительности обратимы немногие. Например, партии в обратные шахматы обычно кончались бы вничью, так как для обратного мата нужен большой материальный перевес, недостижимый в игре близких по силе партнеров. (Рассмотренные в предыдущей главе шахматные поддавки - своеобразная игра, которую нельзя считать обратной шахматам. Правила существенно изменены - королей можно ставить под удар, и они снимаются с доски, как и другие фигуры.)

Очевидно, необратимы все спортивные игры: обращение футбола или хоккея мало бы что изменило (только вратари поменялись бы местами), обратить бокс вообще нельзя и т. д. Это редкое свойство обратимости присуще шашкам благодаря правилу обязательного взятия, без которого игра в поддавки невозможна.

Единство двух шашечных игр подчас не осознается даже квалифицированными шашистами. Один гроссмейстер по шашкам, искусный игрок в поддавки, предложил как-то своим коллегам провести сеанс одновременной игры, пообещав, что выиграет ровно половину партий, остальные же проиграет. Исполнить это намерение гроссмейстер брался даже против мастеров, принявших вызов с уверенностью, что в партиях, которые сеансер собирается выиграть, хоть одну-то ничью они сделают. Однако знатоки классических шашек не сообразили, что их противник может уйти от ничейной угрозы, переключаясь в данной партии на поддавки, где игра на ничью бесперспективна, хотя мирный исход и случается.

Иногда разницы между крепкими и поддавками вообще нет. Взять хотя бы "кооперативные" задачи, которые в шашках в отличие от шахмат почти не составляют. Интересен такой вопрос: какое наименьшее число ходов может продолжаться партия в шашки? Очевидно, нет никакого смысла уточнять, о какой именно игре идет речь - о простой или обратной. Вот рекордная партия, состоящая из десяти ходов: 1. ed4 de5 2. de3 ed6 3. cd2 dc5 4. ab4 c:c1 5. ef4 c:g5 6. fe3 g:b4 7. ab2 e:a1 8. ed2 b:h4 9. gf2 h:el 10. hg3 e:h4. Улучшить этот результат, наверное, нельзя (хотя это и не доказано).

Другую необычную ситуацию можно назвать так: "Ничья и только ничья". Вообще ничьи в крепких и поддавках - вещи разные, потому что в обычной игре речь идет о "ничьей по крайней мере" (если ничья гарантирована, стоит подумать о победе). Иная проблема встала перед бароном Мюнхаузеном, игравшим в шашки в плену на злодейских условиях: выигрыш и проигрыш равно карались смертной казнью, лишь ничья сохраняла жизнь и возвращала свободу. Незаурядная находчивость не подвела Мюнхаузена и на сей раз - в положении на рис. 40, возникшем в процессе поединка "не на жизнь, а на смерть", барон, игравший белыми, проявил исключительное жизнелюбие: 1. db6 hg5 2. cd2 gf4 3. ЬеЗ fg3 4. gf2 gh2 5. ef4 hg1 6. de3 gh2 7. f2-g3 hg1 8. ef2 gh2 9. ed4 hg1 10. f4-e3 gh2 11. ef4, и черные не могут ни проиграть, ни выиграть (что-то вроде позиционной ничьей в шахматах).

Рис. 40

Среди шашистов распространено мнение, будто поддавки по содержательности уступают простым шашкам. Однако есть немало аргументов в защиту поддавков, в том числе количественного характера. Для этого надо установить признаки содержательности, выраженные численно. Прежде всего в содержательной позиции должно быть достаточно много ошибочных ходов (при их отсутствии размышлять не о чем). Отсюда первый признак содержательности: отношение числа ошибочных ходов к числу возможных. Далее, игровые ситуации должны вызывать определенную трудность для общей оценки, производимой без точного расчета. Это обстоятельство оценивается следующим образом. Пусть некоторая позиция выиграна для белых. Немного изменим ее. Новая позиция будет либо по-прежнем,у выиграна за белых, либо уже нет. Во втором случае следует, очевидно, считать первоначальную позицию требующей более внимательного изучения, более содержательной. Малыми изменениями естественно считать, во-первых, передачу хода другой стороне, во-вторых, перемещение одной шашки на соседнее (по горизонтали) черное поле. Это дает два признака содержательности, измеряемые долями позиций с изменившимся исходом среди всех измененных позиций. Передача хода другой стороне дает одну новую позицию, так что второй признак может принимать значения 0 или 1, а третий - чувствительность к малому изменению позиции - меняется в этих пределах. Поясним сказанное на примере (рис. 41).

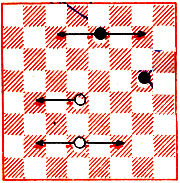
Рис. 41

При игре в крепки любой из четырех ходов белых ведет к ничьей, ошибочных ходов нет. В поддавках выигрывает только 1. de5 и ошибочных ходов три из четырех. При передаче хода черным в простой игре сохраняется ничья, а в поддавках белые уже не выигрывают: 1... gf4 2. dc3 ef6 3. dc5 fe5 4. cd6 e:c7 5. cd4 fg3 6. de5 cd6 7. e:c7 gf2 8. cd8 fg1. Ничья. Переставить одну из шашек на соседнее по горизонтали поле можно (не нарушая разомкнутости позиции) пятью способами, как показано стрелками. В крепких шашках все пять изменений на результат не влияют. В поддавках в двух случаях у белых только ничья. Итак, значения признаков содержательности этой позиции в крепких 0, 0, 0, в поддавках - ³/₄, 1, ²/₅. Сами по себе эти числа еще ни о чем не говорят, ведь единственность хода может быть очевидна, так же как и перемена ситуации после малого изменения позиции. Все же правильность такого подхода более вероятна.

Рис. 42

Конечно, изложенный способ оценки можно применять только ко многим позициям сразу. Это и было проделано для нескольких сот случайно выбранных позиций с малым числом простых шашек. Результаты при оценке разных типов позиций показали хорошую устойчивость: по первому и третьему признакам поддавки немного, а по второму почти вдвое превосходят крепкие шашки. Это, правда, не доказательство, а лишь серьезный довод в пользу обратных шашек, особенно для композиции, где ценятся задачи с единственными ходами. Здесь возможны, в частности, позиции особого рода, о которых говорит известный польский математик Г. Штейнгауз в "Математическом калейдоскопе". В разделе, посвященном шахматной математике, автор предлагает найти позицию, где все ходы обеих сторон были бы единственными непроигрывающими. Ни в шахматах, ни в крепких, похоже, таких позиций не существует. В поддавках же их множество. Вот рекордная по длительности игры, найденная М. Дебецом (рис. 42). Ход белых. 1. с:а5 de3 2. d:f4 g:e3 3. ab2 ed2 4. е:с3 hg5 5. ab6 a:c5 6. gf2 cb4 7. с:а5 gh4 8. bа3 de5 9. ab6 ef4 10. fg3 h:f2 11. bc7 fgl 12. cd8 gd4 13. db6 d:a7 14. ab4 ac5 15. b:d6 fe3 16. dc7 ef2 17. cb8 fg1. Ничья.

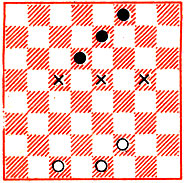
Рис. 43

Какова техника игры в поддавки? Многие принципы и приемы основаны на общих соображениях и совпадают с рекомендациями в крепких шашках, да и не только в этой игре. Владение центром выгодно, на краю доски шашки менее подвижны. Существенно взаимодействие флангов. Надо заботиться о развитии отсталых шашек (a1 и h2 - белым). Важными элементами служат стеснение и угроза. В позиции на рис. 43 после 1. fe3, если хоть на одном из полей, отмеченных крестиками, появится черная шашка, белые сразу завершат игру в свою пользу. По мнению математика И. Бронштейна, немало размышлявшего о поддавках, эта идея стеснения неприятельских шашек легко формализуется и может быть использована при составлении машинной программы для ЭВМ. В нашем примере после 1... ef6 2. cd2 fg7 3. ef2 gh6 4. fg3 белые выигрывают. В течение трех ходов они стесняли черные шашки, и теперь приходится идти на одно из отмеченных полей (4... fg5 5. ef4 g:cl 6. gf4 c:g5; 4... de5 5. ed4 e:h4).

Рис. 44

Теперь приведем пример угрозы (рис. 44). 1. hg3 шах! Употребление шахматного термина здесь вполне уместно. Действительно, угроза немедленно отдать все шашки аналогична угрозе "съесть" короля. 1... аЬ2 2. а:сЗ gf6 3. cd4+ (шах) fg5 (3... cd6 4. dc5 d:b4 5. gf4 + fg5 6. f:h6 и т. д.) 4. ef4 g:c5 5. gf4 cb4 6. fe5 + cb6 7. ed6+ bc5 8. dc7, и появляющаяся на доске белая дамка быстро встает под удар.

Игра в позиции на рис. 43 напоминает засаду, а на рис. 44 - погоню. Так сказать, методы кошки и собаки. В реальной партии, впрочем, далеко не всегда удается различить эти два приема. Отметим, что в поддавках, как и в крепких шашках (но в отличие от шахмат), стеснение играет главную роль, а угроза - вспомогательную.

Материальный перевес в обратной игре, как это ни парадоксально, до поры до времени выгоден. В обычных шашках численное преимущество, очевидно, приближает игрока к конечной цели. Почему же оно полезно и в поддавках? Вот в чем объяснение. Чем больше шашек, тем шире выбор ходов и тем вероятнее, что среди них найдутся выигрывающие. В крепких факторы численности и подвижности действуют в одном направлении, в поддавках - в разных, но роль подвижности остается прежней. Сложение причин, можно сказать, заменяется вычитанием, но фактор подвижности намного важнее. Сущность парадокса заключена именно в этом неожиданном факте, установленном практикой игры. Правда, из того, что численный перевес выгоден, еще не следует, что больший перевес дает большее преимущество.

Играть в крепкие без шашки - все равно, что в шахматы без фигуры. Это интуитивное соображение подтверждается следующим подсчетом. Сумма шахматных сил равна: 9 (ферзь) + 2*4,5 (ладьи) + 2*3,5 (слоны) + 2*3 (кони) + 3 (король) + 8*1 (пешки) =42; и двенадцатая часть их дает 3,5 единицы, то есть слона. Но одна шашка из 12 - это как раз тоже одна двенадцатая часть! Что же касается поддавков, то крайне трудно сказать, в чью пользу снятие одной из шашек.

Рис. 45

Занимательный пример выгоды численного превосходства - игра полным комплектом из 12 шашек против одной шашки соперника. Белые выигрывают в поддавки, если шашка-одиночка занимает одно из полей, отмеченных крестиком на рис. 45. Для выигрыша требуется не более 18 ходов. Рекордная позиция - при черной шашке на е7. Вот основной вариант: 1. cb4! ed6 2. ba5 de5 3. ef4 ed4 4. fe5 d:f6 5. de3 fe5 6. ef4 ed4 7. fe3 d:h4 8. ab4 hg3 9. bc5 g:e5 10. cd6 e:c7 11. ab6 c:a5 12. cd2 ab4 13. bс3 bа3 14. hg3 ab2 15. gf2 b:d4 16. fe3 d:h4 17. ab2 hg3 18. ef2 g:hl.

В качестве комментария к этой партии можно привести шуточный "Гимн поддавкам" известного поэта Н. Глазкова:

Если иногда играю в шашки,
То предпочитаю поддавки!
В поддавках есть четкость светофора,
И веселость шашки проходной,
И изящество обратной формы -
Все двенадцать супротив одной!

Рис. 46

На рис. 46 показано, в каких случаях решается аналогичная задача выигрыша в поддавки на 100-клеточной доске - 20 шашками против одной. Любопытно, что соответствующее доказательство было опубликовано Бельгийской Академией наук еще в 1852 году, причем его автор рассмотрел более 800 различных вариантов.

При умелой игре в поддавки рано или поздно наступает переломный момент, когда надо отдавать завоеванный материал. Однако подставлять шашки под удар лишь затем, чтобы их стало меньше, неразумно на любой стадии игры; всегда надо готовить почву для избавления от всех сразу. Если выгоду отдачи материала не удается доказать анализом, то это жертва. Например, после 1. ed4 bc5 2. d:b6 c:a5 3. cb4 а:с3 4. b:d4 ab6 5. fe3 ba5 (рис. 47) белые на практике часто жертвуют шашку: 6. аb4 а:е5 7. dc3 ed4 ? 8. с:с7. Черным предстоит решать весьма не простые проблемы развития.

Рис. 47

Еще один важный прием борьбы - запирание чужих шашек. В нужный момент они выпускаются на свободу, и партия заканчивается победой того, кто сумел их вовремя запереть.

Примером того, что поддавки - не чисто счетная игра (а многие так думают), может служить партия Болдин-Бронштейн. 1. gh4 hg5 2. ef4 g:e3 3. f:d4 bc5 4. d:b6 c:a5 (распространенное начало) 5. gf2 fe5 (уходя от запирания на h4) 6. cb4 a:c3 7. b:f6 g:e5 8. dc3 (фиксируя слабую шашку е5) 8... Ьс7 (правильно 8... ed4, теперь черные попадают в цугцванг) 9. ab2 hg7 10. ab4 аb6 11. cd2 ef6 12. hg5 f:h4 13. cd4 e:a5 14. hg3 ab4 15. dc3 b:d2 16. e:c3 gf6 17. cb4, и белые одну за другой отдают все свои шашки.

Рис. 48

Ничьи в поддавках бывают редко. Дамки разного цвета на полях b8 и b2 - часто встречающийся ничейный финал. Рекордная по числу шашек ничейная позиция зафиксирована в партии Ларин - Родзянко (рис. 48): при ходе белых единственно непроигрывающие перемещения - 1. cd6 bc5 2. dc7 cb6 и т. д.

В обычных шашках в выигранной позиции среди ошибочных ходов, скорее всего, найдутся и ничейные. В поддавках ошибка обычно ведет к поражению, то есть ничейной полосы между зонами выигрыша и проигрыша может не оказаться. Поэтому нельзя избежать риска, уклоняясь от сложных и острых позиций,- в простых и спокойных на вид его не меньше. Кстати, отсутствие ничейной полосы создает трудности комментатору партий. Стандартная оценка "с преимуществом у..." означает, что преимущества может не хватить для победы - иначе следовало бы сказать "с выигрышем". В поддавках невозможность выиграть часто чревата поражением, в таких условиях говорить о преимуществе вряд ли уместно. Аналогичные соображения возникают и по поводу оценки "с примерно равной игрой". Так что от "ничейной смерти" поддавки, видимо, надежно застрахованы.

Дебютная теория обратной игры постепенно развивается, ограничимся самыми краткими сведениями. Из семи возможных первых ходов наиболее часто используются 1. ed4 и 1. gh4, за ними следует 1. аb4. Можно считать доказанным, что начала 1. ef4 и 1. gf4 ведут к форсированному поражению белых после ответа 1... hg5. Ходы 1. сb4 и 1. cd4 возможны, но статистика встреч между опытными игроками показывает, что игра чаще складывается в пользу черных.

В поддавки на стоклеточной доске играют, естественно, по правилам международных шашек. Различия, возникающие при переходе на большую доску, здесь гораздо существеннее, чем в простых шашках, но это уже другая тема...

Почему же поддавки уступают в популярности обычным шашкам?! Видно, причина в традиционном взгляде на шашечную игру как на модель военных действий. Стремление уничтожить или пленить силы противника, характерное для большинства игр, в том числе шашечных, более привлекательно своей жизненностью. Впрочем, перечитывая "Опыты" М. Монтеня, мы обнаружили исторический эпизод, который служит вполне реальным аналогом обратной игры...

"Александр осаждал какой-то город в Индии. Жители, доведенные до крайности, твердо решили лишить его радости победы; они подожгли город и вместе с ним все погибли в пламени, презрев великодушие победителя. Началось новое сражение: враги дрались за то, чтобы их спасти, а жители за возможность покончить с собой, причем прилагали к этому такие же усилия, какие люди обычно делают, чтобы спасти свою жизнь".