Математические игры на шахматной доске

Необычные игры на шахматной доске придумывают не только шахматные композиторы-фантасты, но и математики. Правда, последние предпочитают игры, допускающие, математический анализ; изложенные в виде задач, они предлагаются на математических олимпиадах или включаются в различные сборники.

В математических играх интерес представляет нахождение четкого алгоритма, гарантирующего победу или ничью. Но если алгоритм уже найден, то процесс игры теряет творческий характер, столь привлекающий нас в интеллектуальных играх.

Любопытно, что в эпоху Возрождения была очень популярна специальная шахматно-математическая игра "арифметические шахматы", или, иначе, рифмомахия. На доске 16*8 передвигались три рода фигур - в форме круга, треугольника и прямоугольника. На каждой фигуре были написаны числа, комбинации которых определяли ходы, взятия и объявление мата. Игра требовала слишком сложных математических расчетов и постепенно была забыта.

Конь и верблюд. В углу доски n*n (n≥4) стоит конь, которым противники ходят по очереди. Первый игрок перемещает его как обычного коня, но с двойным ходом (как в двухходовых шахматах), а второй - как верблюда, то есть на три поля вдоль одной линии и на одно поле - вдоль другой. "Белые" начинают и стремятся поставить фигуру в противоположный угол доски, а "черные" стараются помешать им. Чем закончится игра?

В этом несколько странном соперничестве коня и верблюда (точнее было бы говорить о хамелеоне, превращающемся то в одну фигуру, то в другую) победителем выходит обычный конь! Если наша фигура стоит на большой диагонали, проходящей через исходное угловое поле, то на любое отступление верблюда с этой диагонали конь возвращается на нее, причем продвигается по крайней мере на одно поле ближе к цели. В конце концов он попадает в нужный угол.

Кошки-мышки. У первого игрока всего одна фигура - мышка, а у другого несколько фигур - кошек. Мышка и кошки ходят одинаково - на одно поле по вертикали или горизонтали, то есть получаются из коня (а, b) при а = 0, b = 1. Если мышка оказалась на краю доски, то очередным ходом она спрыгивает с нее и убегает от кошек; если кошка и мышка попадают на одно поле, то кошка съедает мышку.

Борьба кошек с мышкой протекает на обычной шахматной доске, причем играющие ходят по очереди и второй из них передвигает одним ходом сразу все свои кошки (в любых направлениях). Начинает мышка, которая старается спрыгнуть с доски, а кошки хотят ее съесть. Возможны два варианта игры, для каждого из которых сформулируем интересную задачу.

• Кошек всего две, а мышка стоит на внутреннем поле доски. Можно ли так расположить кошек на краю доски, чтобы в конце концов они сумели съесть мышку?
• Кошек три, стоят они где угодно, но зато мышка на первом ходу делает два хода подряд. Сможет ли мышка убежать от кошек?

Покажем, что в первом случае мышке не уйти от погони, а во втором, наоборот, она благополучно убегает от кошек.

• Через поле, на котором стоит мышка, проведем какую-нибудь диагональ и поставим кошек на ее конце. На каждый ход мышки кошки ходят так, чтобы все три фигуры снова оказались на одной диагонали, а расстояние между кошками сократилось на одно поле (по диагонали). Такая стратегия позволяет кошкам в скором времени съесть мышку.
• Рассмотрим две диагонали доски, проходящие через поле, занятое мышкой. Если поле не крайнее (иначе мышка сразу спрыгнет с доски), то эти диагонали разбивают доску на четыре части. Поскольку кошек три, внутри одной из частей их нет. Проведем перпендикулярный отрезок (горизонтальный или вертикальный), соединяющий мышку с краем доски внутри этой части. Очевидно, если мышка отправится прямо вдоль этого отрезка к краю доски, то кошкам ее не догнать.

Ферзя - в угол. На доске стоит ферзь, которого два игрока по очереди передвигают на любое число полей либо вверх, либо вправо, либо вверх и вправо по диагонали (то есть отступать ферзем нельзя). Выигрывает тот, кто своим ходом загоняет ферзя в правый верхний угол доски - на поле h8.

Рис. 37

Покажем, что результат игры автоматически определяется из рис. 37. Если ферзь стоит на поле с плюсом, то выигрывает тот, чей ход, а если на поле с минусом, то его партнер. Ничьей в этой игре не бывает. Пусть ферзь находится на восьмой горизонтали, вертикали "h" или диагонали a1-h8 (кроме поля h8), тогда белые первым же своим ходом ставят ферзя в угол и берут верх. Далее рассуждаем так. Если ферзь с данного поля доски вынужден пойти на поле с плюсом, то оно, естественно, получает минус, а если ферзь может пойти на "минус", то оно получает плюс и т. д. В конце концов на всех полях доски будут расставлены знаки. В результате оказывается, что семь полей являются проигранными для начинающей стороны, а остальные выигранными, причем ферзь попадает в желанный угол не позднее третьего хода. Пусть в начале игры ферзь стоит на поле Ы (см. рис. 37), тогда "партия" может протекать так: 1. Фb1-d1 (быстрее к цели вело 1. Фg6!) 1... Фd2 2. Фd3! (единственный ход) 2... Фd7 3. Фf7! Фh7 4. Фh8 с победой.

Указанный принцип расположения плюсов и минусов переносится на любую прямоугольную доску, то есть на каждой из них игра подвергается исчерпывающему анализу.

Возьмем теперь вместо ферзя ладью и рассмотрим игру "ладью в угол". По своим правилам эта игра аналогична предыдущей, а по алгоритму напоминает "коня и всадника"! Игроки по очереди перемещают ладью по горизонталям (вправо) и вертикалям (вверх), и побеждает тот, кто первым займет угловое поле h8.

Вновь на h8 ставится минус, а все остальные поля восьмой горизонтали и вертикали "h" получают плюс. При ладье на g7 начинающий проигрывает - минус, а на остальных полях седьмой горизонтали выигрывает - плюс и т. д. В результате получаем, что "белые" выигрывают, если их ладья не стоит на диагонали a1 - h8. Метод выигрыша тот же, что и в игре "конь и всадник". Первым ходом надо занять "большую" диагональ, после вынужденного отступления противника снова вернуться на нее - и так, пока ладья не попадет в угол. Самая длинная партия при исходном положении ладьи на поле а2 или Ы состоит из семи ходов: 1. Лb1-b2! Лс2 2. Лс3 Лс4 3. Лd4! Ле4 4. Ле5! Ле6 5. Лf6! Лg6 6. Лg7 Лg8 7. Лh8.

Аналогично анализируются игры "коня в угол" и "короля в угол". Теория таких игр легко переносится на любые доски. Для того чтобы оценить положение, достаточно правильно расставить на доске плюсы и минусы.

Шахматы и игра "ним". Вот еще одна игра с ладьями. Возьмем произвольную доску m*n. Пусть на ее первой горизонтали стоят белые ладьи, а на последней - черные. Игроки ходят по очереди ладьями по вертикалям (вперед или назад), и выигрывает тот, кто прижимает все m ладей противника к краю доски.

Теперь немного отвлечемся и рассмотрим другую "игру двух лиц". Имеется несколько кучек камней, и каждый ход игрока заключается в том, что он берет из какой-нибудь кучки произвольное число камней. Ходят по очереди, и побеждает тот, кто забирает последние камни. Эта старинная игра называется ним, она описана в любой книге по занимательной математике. Существует огромное количество модификаций нима. В одних играх накладываются ограничения на число камней, которые можно брать, в других - разрешается перекладывать камни из кучки в кучку, в третьих - камни можно брать сразу из нескольких кучек и т. д. В игре нимби кучки три с числом камней соответственно 3, 4 и 5. Эти двенадцать камней располагаются на клетках специальной доски и могут забираться по определенным правилам. В игре Баше камни берутся из одной кучки, но не больше заданного количества, в игре цзяньшицзы кучки две, а камни можно брать не только как в обычном ниме (любое число из одной кучки), но и сразу из двух кучек - в этом случае одинаковое число. Как правило, в каждом варианте нима удается провести тонкий математический анализ и найти правильный метод игры.

Вот "детский" вариант нима с одной кучкой камней (спичек), которую легко усваивают и дошкольники. Двое по очереди берут из кучки один, два или три камня. Побеждает тот, кто берет последний камень. Очевидно, если вы оставите противнику 4 камня, а перед этим 8, 12 и т. д., то победа будет за вами. Таким образом, начинающий выигрывает, если число камней в кучке не делится на 4, если же оно кратно четырем, то побеждает второй игрок. Читатель, наверное, уже сообразил, что.игра с ладьями представляет собой одну из разновидностей нима. Роль кучек камней здесь играют вертикали доски, а количество камней в кучке равно числу полей между ладьями на соответствующей вертикали. Итак, в начале игры мы, по существу, имеем m кучек, и в каждой по n-2 камня. Ход ладьи есть не что иное, как удаление нескольких камней из кучки (если ладья приближается к ладье противника) или добавление камней (если ладья удаляется от ладьи противника).

Оказывается, для оценки результата игры в таком варианте нима имеет значение только число вертикалей доски, а сколько горизонталей - неважно (лишь бы их было не две, иначе белые проигрывают, не начав игры). Если число вертикалей нечетно, то выигрывают белые, а если четно, то черные. Если доска состоит всего из одной вертикали, белые первым же ходом прижимают неприятельскую ладью (забирают все камни из кучки), и партия заканчивается в их пользу. Пусть вертикалей две - а и b. Тогда на любой ход белой ладьи вперед черные отвечают центрально-симметричным ходом, и эта стратегия приводит их к цели. Например: 1. Ла3 Лb6! 2. Лb4 Ла5! 3. Ла4 Лb5! Теперь белые ладьи o вынуждены отступать, и черные преследуют их до победного конца (конечно, при отступлении белых ладей черным уже незачем соблюдать симметрию). На доске 3*8 белые играют 1. Лс7! и сводят игру к предыдущему случаю при ходе противника. Симметричные действия на первых двух вертикалях приносят им побг На доске 4*8 опять выигрывают черные и т. д.

Поговорим еще раз о ниме. Если кучек камней всего две, то анализ игры прост. Пусть в одной кучке s камней, а в другой t(s>t). Возьмем при своем ходе из первой кучки s-t камней, то есть уравняем их. Дальше будем действовать симметрично - сколько бы камней ни взял противник из одной кучки, столько же возьмем из второй и т. д. Очевидно, если в начале игры s = t и мы начинаем, то наше дело плохо.

Эта игра почти не отличается от игры с ладьями. При s>t начинающий первым же ходом сводит ее к перемещению ладей на доске 2*(t+2) при ходе партнера и выигрывает. Конечно, в данном случае обращение к шахматам не обязательно. А вот в следующей игре оно очень полезно.

Пусть кучек по-прежнему две, но камни можно брать не только из одной кучки, а сразу из двух, но в этом случае обязательно поровну, то есть мы получаем вариант нима, называемый цзяньшицзы. Предположим, что в первой кучке семь камней, а во второй - шесть. Возьмем тогда шахматную доску и поставим на поле b1 ферзя (рис. 37). Как видно, выше ферзя находятся семь горизонталей, а правее шесть вертикалей.

Установим соответствие между ходами в двух наших играх - цзяньшицзы и "ферзя в угол". Взятию некоторого числа камней из первой кучки соответствует перемещение ферзя на столько же полей по вертикали, а взятию из второй кучки - по горизонтали; наконец, если из обеих кучек берется одинаковое число камней, то ферзь идет по диагонали на то же число полей. В тот момент, когда от кучек ничего не останется, ферзь попадает в угол доски.

Итак, нам не нужно разрабатывать теорию для цзяньшицзы, а следует воспользоваться теорией для игры "ферзя в угол". В нашем примере ферзь стоит на поле с плюсом, и поэтому начинающий выигрывает. В общем случае, при произвольных наборах камней в кучках, для оценки позиции в цзяньшицзы достаточно "перевести" ее на шахматную доску и посмотреть, на какое поле попадет при этом ферзь (иной вопрос - будет ли обозрима такая доска)!?.

Итак, различие между двумя рассмотренными играми чисто внешнее: позиции и ходы в одной из них соответствуют позициям и ходам в другой. Такие игры математики называют изоморфными.

Похожую игру с камнями придумал выдающийся советский математик академик И. Гельфанд. Снова имеются две кучки камней, но брать теперь можно либо один камень из первой кучки, либо один из второй, либо два камня по одному из каждой кучки, наконец можно не брать камни, а переложить один камень из одной кучки в другую. По-прежнему выигрывает тот, кто забирает последний камень.

И эта игра изоморфна шахматной, аналогичной "ферзя в угол". Только роль ферзя, как нетрудно проверить, в данном случае играет король. Расставляя необходимым образом плюсы и минусы на доске 8*8, легко провести исчерпывающий анализ игры.

Домино на шахматной доске. По своей природе домино имеет более близкое отношение к математике, чем многие игры, о которых рассказывается в нашей книге. Числа, изображаемые точками на костях домино, присутствуют здесь в явном виде. В литературе по занимательной математике можно найти десятки комбинаторных задач, головоломок, фокусов и игр с домино. Особенно популярны "кадрили" - раскладывание на столе костей домино, обладающее теми или иными хитрыми свойствами.

Например, интересна такая игра. Два игрока по секрету друг от друга раскладывают весь набор из 28 костей в виде прямоугольника 8*7. Затем они переписывают расположение своих чисел на листе бумаги и вручают их друг другу.

Границы между костями домино теперь стерты, и игрокам надо определить, как они были расположены у противника, то есть разбить числовой прямоугольник 8*7 на 28 прямоугольников 2*1, образующих полный набор домино. Кто раньше это сделает, тот и побеждает.

Разумеется, эта игра и всевозможные "кадрили" не имеют прямого отношения к классическому домино, в котором содержится немало тонкостей, есть даже свои мастера. Однако успех, как нам кажется, прежде всего зависит от наблюдательности (кто на "что" играет), а не от математических способностей. Заметим, что известно множество игр, отличающихся от традиционного домино. Вот некоторые из них: молния (за один ход можно выставить несколько костей, стыкующихся между собой); слепое домино (игроки не видят собственные кости и вскрывают их одну за другой по ходу дела); берген (за каждый ход игроки получают определенное число очков, и выигрывает тот, кто первым набирает заданную сумму); пятерочное домино, троечное домино, магинз, Севастополь, китайское домино, юбилей, сорок два, матадор и т. д.

В заголовке этого раздела у нас фигурировала шахматная доска, так что пора оправдать название. Приведем знаменитую головоломку, в которой участвуют одновременно и доска, и домино.

Из квадратной доски 8*8 вырезаны два угловых поля, лежащие наискосок друг от друга,- а1 и h8. Можно ли оставшуюся часть квадрата покрыть целиком 31 костью домино (то есть прямоугольниками 2*1)?

Можно было бы воспользоваться алгебраическими рассуждениями, но "шахматное" решение и проще, и изящнее. Раскрасим наш урезанный квадрат в черно-белый цвет в шахматном порядке. Теперь обратим внимание на то, что на полученной доске вырезаны два поля одного цвета, и на ней черных полей осталось на два меньше, чем белых. Но ведь каждая кость домино покрывает одно белое и одно черное поле, и, значит, необходимого покрытия всей доски не существует!

Конечно, непосредственно к играм эта задача имеет отдаленное отношение, но трудно было удержаться, чтобы не привести столь эффектный пример...

Кстати говоря, именно эта задача породила целый класс математических развлечений - полимино, упомянутый нами в рассказе о морском бое. Полимино - это не только увлекательные головоломки, в которых необычные доски нужно покрывать прямоугольными фигурками, но и игры для двух человек. Вспомним сначала следующую забавную игру-задачу.

На идеально круглом столе двое играющих по очереди выкладывают монеты любого достоинства. Проигрывает тот, кто при очередном ходе не может положить монету так, чтобы она не выступала за край стола и не наложилась на другие монеты.

Результат этой игры предопределен еще до ее начала. Выигрывает начинающий, причем победу ему обеспечивает симметричная стратегия. Первым ходом белые должны положить произвольную монету в центр стола, после чего им остается только копировать ходы противника: на всякий его ход класть монету того же достоинства на центрально-симметричное место. Если черные еще в состоянии положить какую-то монету на стол, то и для монеты белых того же достоинства на столе найдется свободное центрально-симметричное место. В конце концов настанет момент, когда второй игрок не сможет сделать ход, и партия за -кончится его поражением.

Очевидно, такая симметричная стратегия приводит к цели не только при игре на круглом столе, но и на квадратном, прямоугольном и вообще на столе любой формы, представляющем собой центрально-симметричную фигуру. Вместо монет могут быть взяты произвольные фишки, лишь бы их было в достаточном количестве.

Ясно, что описанная игра с монетами носит, так сказать, умозрительный характер. Трудно представить себе двух игроков, которые бы запаслись толстыми кошельками и по очереди выкладывали монеты на стол...

Более серьезно обстоит дело в играх полимино на шахматных досках размером m*n. Двое играющих кладут по очереди домино на доску, покрывая каждой костью два поля доски. Как и в игре с монетами, проигрывает тот, кто не может сделать свой очередной ход. И в этой игре знакомые нам идеи симметрии имеют решающее значение. Возьмем доску 10*6. Стратегия игры здесь та же самая, что и в игре с монетами, но на этот раз начинающий проигрывает. Второму игроку не надо ни о чем заботиться, а достаточно копировать (центрально-симметрично!) ходы партнера. Так, если начинающий делает ход 1 (рис. 38 а), то второй игрок кладет кость 2, на ход 3 отвечает 4, на ход 5-6 и т. д. до тех пор, пока первый игрок не сможет сделать ход.

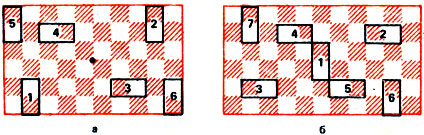
Рис. 38

Если одна из сторон доски четная, а другая нечетная, то выигрывают уже белые. Например, на доске 11*6 они первым ходом кладут кость в центр доски и далее действуют описанным методом, полностью сохраняя симметрию. Первые несколько ходов показаны на рис. 38 б; вновь нечетные номера принадлежат первому игроку, а четные - второму.

Отметим, что если обе стороны доски нечетны, то симметричные действия уже не гарантируют успеха. Оптимальная стратегия для такой доски нам не известна. Кстати говоря, если играть в домино (или произвольный набор полимино) на доске, которая разделена на квадраты (поля), и, значит, фишки разрешается класть куда угодно, то это уже ничем не будет отличаться от игры в монеты. Начинающий всегда выигрывает независимо от четности сторон доски - ему достаточно первым ходом занять домино центр доски и дальше, как обычно, придерживаться центрально-симметричной стратегии.

Симметрия в шахматах. Мы уже убедились на ряде примеров (полимино, игра с ладьями), что симметричная стратегия часто приводит к цели. А как обстоят дела с самими шахматами? Может быть, черным достаточно просто копировать ходы белых и такая стратегия обеспечит им ничью? Как показывает следующая забавная партия, черным может неожиданно повезти.

1. е4 е5. Очевидно, в шахматной партии возможна лишь осевая симметрия - начальная позиция симметрична относительно прямой, разделяющей нижнюю и верхнюю части доски. 2. Кре2 Кре7 3. Кре3 Кре6 4. Фf3 Фf6 5. Ке2 Ке7 6. b3 b6 7. Са3 Са6 8. Kd4+ . Королю черных объявлен шах. Выбора нет, они вынуждены нарушить симметрию и... объявить мат после 8... ed*!

Партия получилась забавной, но, как вы понимаете, если бы черные, копируя ходы противника, могли взять верх или хотя бы добиться ничьей, то вряд ли бы так часто разыгрывалось первенство мира по шахматам!

Известна такая забавная история. Некто явился в шахматный клуб и объявил, что нашел верный способ не проигрывать черными. "Каким образом?"- спросили его. "Очень просто,- ответил гость,- повторяя ходы противника!" Сыграть с наивным изобретателем вызвался Сэм Лойд. Партия продолжалась всего четыре хода: 1. с4 с5 2. Фа4 Фа5 3. Фc6 Фс3 4. Ф:с8*. Возможно, если бы партнеры сели играть вновь, дело закончилось бы несколько иначе: 1. d4 d5 2. d3 d6 3. Фb3 Фb6 4. Ф:с8*.

Подобные шахматные "поединки", в которых черные полностью копируют ходы противника и в конце концов получают мат, называются обезьяньими партиями. В приведенных примерах мат ставил белый ферзь, и быстрее ср своей задачей он справиться не мог. А каковы рекорды обезьяньих партий, в которых мат дается другими фигурами - ладьей, слоном, конем и пешкой?

В начале века этим вопросом интересовался шахматный композитор К. Тракслер. Он составил симметричные партии, где ладья ставила мат за 9 ходов, слон - за 8, конь - за 7 и пешка - за 15 ходов. Эти рекорды неоднократно улучшались, и в дальнейшем , были придуманы партии, в которых ладья матует за 8 ходов, слон - за 7, конь - за 6 и пешка - за 7 ходов. Вот самые короткие обезьяньи партии.

Матует ладья: 1. Kf3 Kf6 2. Kg5 Kg4 3. K:h7 K:h2 4. K:f8 K:fl 5. Kg6 Kg3. Танец коней закончился. 6. Л:h8*.

Матует конь: 1. Кс3 Кс6 2. Ке4 Ке6 3. е3 е6 4. Ке2 Ке7 5. g3 g6 6. Kf6* (или 5. с3 с6 6. Kd6*).

Матует белопольный слон: 1. е4 е5 2. f4 f5 3. ef ef 4. f6 f3 5. fg fg 6. Ce2 Ce7 7. Ch5*, и теперь чернопольный : 1. d4 d5 2. Kpd2 Kpd7 3. Kpd3 Kpd6 4. Сс3 Сс6 5. с3 с6 6. Фd2 Фd7 7. Cf4*.

Наконец, матует пешка: 1. g4 g5 2. h4 h5 3. Kf3 Kf6 4. Ke5 Ke4 5. hg hg 6. g6 g3 7. gf*; или 1. f4 f5 2. g4 g5 3. gf gf 4. f6 f3 5. Kh3 Kh6 6. Kg5 Kg4 7. f7*.

Наше лирическое отступление, посвященное обезьяньим партиям, относится, скорее, к жанру юмора, хотя, как мы видели, мотивы симметрии присутствуют и здесь.

Среди игр, придуманных сравнительно недавно, следует выделить два интересных класса - топологические игры и игры на графах. Возникновение этих игр, по-видимому, объясняется бурным развитием двух современных разделов математики - топологии и теории графов. К сожалению, в структуру нашей книги (учитывая ее объем) эти игры не очень вписываются. Очевидно, и к шахматам они не имеют отношения. Упоминание в данной главе объясняется тем, что оптимальной стратегией в них часто служит симметрия.

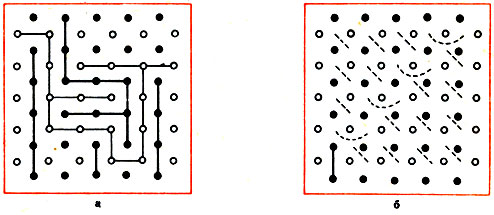
Рис. 39

Возьмем, к примеру, игру бридж-ит. На рис. 39а показана "доска" для этой игры. Участники по очереди проводят вертикальные и горизонтальные отрезки, соединяя ими точки своего цвета. Линии противников нигде не должны пересекаться. Выигрывает тот, кто первым построит ломаную своего цвета, связывающую противоположные стороны доски (на рис. 39а победили белые).

Оптимальную стратегию, гарантирующую победу белым в бридж-ит, открыл О. Гросс, специалист по теории игр. Эта стратегия столь же эффектна, сколь и проста. Воспользуемся рис. 39 б. Первым ходом соединим две точки в левом нижнем углу. Дальше надо играть так: каждый раз, когда отрезок, проведенный противником, пересекает конец какой-нибудь пунктирной кривой, следует провести отрезок, пересекающий второй конец той же кривой, и так вплоть до победы. Эта остроумная стратегия легко обобщается на любую доску.

Обратите внимание, что на рисунке заранее не предусмотрены линии, соединяющие граничные точки доски. Правила игры в бридж-ит не запрещают такие линии, но проводить их бессмысленно; если ваш противник вдруг проводит отрезок вдоль границы доски, то надо сделать контрход, соединив либо две граничные, либо, если это больше нравится, любые две точки доски. Может оказаться, что именно этот случайный ход будет потом продиктован стратегией, тогда, поскольку вы его уже сделали, проведите любую другую линию, лишняя линия на доске никогда не будет помехой. Разумеется, теперь, когда известна оптимальная стратегия для первого игрока, бридж-ит утрачивает свою привлекательность.

К сожалению, мы вынуждены оставить в стороне такие интересные топологические и графовые игры, как "рассада", "брюссельская капуста", "гекс", "игра в точки", "переключательная игра Шеннона", и др.

В заключение главы отметим, что рассмотренные нами стратегии, когда на каждый ход одного партнера автоматически следует ход другого (и этот ход приближает к цели!), в теории игр называются парными.

Любопытные примеры симметричной игры и парной стратегии будут приведены также в следующих главах.