Морской бой

Не каждому читателю приходилось играть в "быки и коровы" или "отгадать слово", но человека, который ни разу в жизни не сражался в "морской бой", наверное, не найти. Несмотря на внешнюю простоту, эта популярная игра и ее различные модификации содержат немало тонкостей.

Классический морской бой. Начнем с самого популярного варианта морского боя, распространенного во многих странах. Каждый из двух игроков рисует на клетчатом листе бумаги две доски размером 10*10. На первой из них он расставляет свои корабли, а на второй разгадывает расположение кораблей противника. В состав флотилии входят десять кораблей: один линкор (корабль 4*1), два крейсера (3*1), три эсминца (2*1) и четыре катера (1*1). Корабли могут занимать любые поля доски, но не должны касаться друг друга ни сторонами, ни углами.

После размещения флота игроки начинают по очереди стрелять по неприятельской территории, то есть называть поля доски - а3, б7, и9 и т. д. (горизонтали доски будем обозначать числами от 1 до 10, а вертикали - русскими буквами от а до к - см. рис. 6 и 7). После каждого выстрела игрок получает от партнера следующую информацию: "попал", если выстрел пришелся по полю с кораблем; "убил", если это последнее поле корабля (по другим полям, занятым им, попадание произошло раньше); и наконец, "мимо", если поле пустое. В первых двух случаях игрок производит еще один выстрел, и так до первого промаха, после чего очередь хода передается партнеру. Побеждает тот, кто первым потопит все десять кораблей противника.

Таким образом, в данной тестовой игре шифром служит набор прямоугольников, расположенных на доске, а самим тестом - удары по ней. Обычно выстрел в морском бое обозначается точкой, а при попадании в корабль точка превращается в крестик (сам потопленный корабль обводится прямоугольником). Конечно, точки ставятся и на те поля, про которые уже точно известно, что они не могут входить в состав ни одного из кораблей (лежат наискосок от "подбитых" полей или окружают потопленный корабль).

Различные доски и корабли. Очевидно, форма доски в морском бое, вид кораблей и состав флотилии особого значения не имеют. Так, шахматисты, возможно, предпочтут играть на доске 8*8. Заметим, что в терминах игры "полимино" наши корабли имеют такие названия: катер - мономино, эсминец - домино, крейсер - прямо тримино, линкор - прямое тетрамино (рис. 2). В качестве кораблей в этой игре можно использовать и другие виды полимино. На рис. 2 представлены все девять кораблей, содержащих не более четырех клеток.

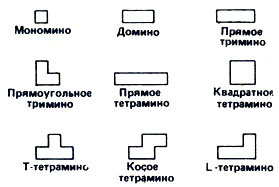
Рис. 2

Сражение можно вести не только на море, но и на суше. Для этого доску следует разбить на две части - морскую и береговую. Противники получают в свое распоряжение три вида боевых средств - флот (корабли могут располагаться только в море), сухопутные войска (размещаются на суше) и самолеты, которые находятся как в море, так и на суше. Можно, например, использовать для игры 20 боевых единиц: во флотилию включить десять кораблей обычного морского боя, в сухопутные войска - два квадратных, два косых, два Т- и два L-тетрамино и, наконец, два прямоугольных тримино превратить в самолеты. Одно из расположений всех видов войск на доске 20*15 представлено на рис. 3 (береговая часть доски на рисунке заштрихована). Как и положено, флот находится в море, а сухопутные войска дислоцированы на суше, один самолет летает над морем, другой охраняет берег.

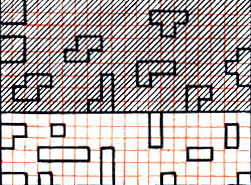
Рис. 3

Вот еще одна разновидность морского боя. Игра протекает на шахматных досках 8X8; каждый из двух игроков разбивает свою доску на четыре части произвольной формы, состоящие из одинакового количества полей - по 16 каждая. На рис. 4 даны четыре варианта разбиения доски. Ход состоит из четырех одновременных выстрелов по полям доски, образующим произвольный квадрат 2*2, например б5, б6, в5, в6 (на рис. 4 его поля помечены крестиками). Обстреливаемый игрок сообщает номера частей, в которые произошло попадание, не указывая при этом, какие поля каким частям принадлежат. Для наших квадратов ответы будут такие: 2, 2, 2, 3 - рис. 4а; 1, 1, 2, 2 - рис. 4б; 2, 2, 3, 4 - рис. 4в; 2, 2, 3, 3 - рис. 4г. После каждого хода партнеры делают определенные выводы о возможном разбиении доски и на их основании выбирают следующий ход. Побеждает игрок, который первым определяет, на какие четыре части разбил противник свою доску.

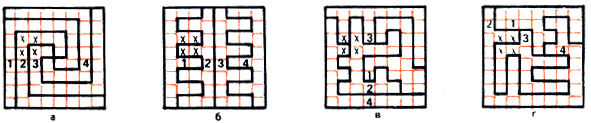
Рис. 4

Стратегия игры в морской бой. Вернемся к обычному морскому бою на доске 10*10. Конечно, успех здесь, как и в предыдущих тестовых играх, в какой-то мере зависит от везения. Можно беспорядочно наносить удары по неприятельской территории и при этом без промаха уничтожить все его корабли. Но вряд ли на это стоит рассчитывать. Если говорить об искусстве игры в морской бой, возникают два вопроса: 1) как стрелять, чтобы повысить вероятность попадания в неприятельские корабли; 2) как расставлять собственные корабли, чтобы противнику было труднее их потопить?

Предположим, мы хотим попасть в неприятельский линкор. Если cтрелять последовательно сначала по полям первой горизонтали (слева направо), затем по полям второй и т. д., не исключено, что мы обнаружим его только после 97-го удара (если корабль занимает поля с ж10 по к10). Однако, стреляя по полям, обозначенным крестиками на рис. 5а или 5б, мы наверняка попадем в линкор не позднее 24-го удара (24 крестика следуют друг за другом через три поля вдоль каждой вертикали и горизонтали).

Рис. 5

Рассмотрим более общий случай. Предположим, что на доске n*n расположен один-единственный корабль к*1 (к-мино). Совокупность выстрелов, гарантирующих нам попадание в этот корабль, назовем стратегией. Стратегию, содержащую минимальное число выстрелов, назовем оптимальной; число выстрелов в ней обозначим через s (n, k).

Очевидно, s (4, 4) = 4; все семь оптимальных стратегий для доски 4*4 представлены на рис. 6 (стратегии, которые совпадают при поворотах и зеркальных отражениях доски, мы не различаем). Сдвигая все выстрелы на четыре поля по вертикали и горизонтали, получаем семь стратегий на доске 10*10. Однако только две из них являются оптимальными (рис. 5,а и 5,б сравните с рис. 6,а и 6,б), причем s (10, 4) = 24.

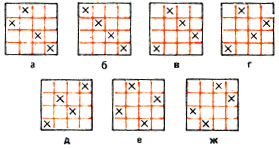
Рис. 6

Ясно, что для попадания в корабль k*1, расположенный на доске n*n, выстрелы должны отстоять друг от друга на k полей по вертикали и горизонтали. Это означает, что на каждой линии содержится примерно по ⁿ/_k выстрелов оптимальной стратегии, и мы получаем приближенную формулу s(n, k)≈ ⁿ²/_k

Опытные игроки обычно действуют следующим образом. Сначала, пользуясь одной из стратегий на рис. 5, обнаруживают единственный линкор противника. Когда с ним будет покончено, принимаются за поиск крейсеров. Теперь удары наносятся не через три поля по вертикалям и горизонталям, а через два. Потопив оба крейсера, переходят к эсминцам. Когда непотопленными останутся одни катера, выбор полей ударов уже не будет иметь никакого значения, и приходится полагаться только на случай. Конечно, "легкие" корабли могут быть обнаружены и при охоте за "тяжелыми".

Итак, труднее всего обстоит дело с катерами, для нахождения которых нельзя придумать эффективной стратегии. Поэтому при размещении собственной флотилии надо располагать все крупные корабли поплотнее, представляя противнику для поиска катеров как можно больше свободной территории. Наиболее выгодное в этом смысле размещение показано на рис. 7. Если даже соперник потопил все шесть наших крупных кораблей, для обнаружения четырех катеров у него имеется территория наибольшей площади - целых 60 полей (на рисунке справа от черты).

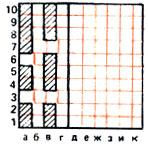
Рис. 7

Напряженный бой. Рассмотрим интересный "эндшпиль", в котором одна неточность сразу решает исход боя (этот пример придумал В. Чванов).

На рис. 8 изображено положение, возникшее в процессе игры. К данному моменту обе флотилии - и наша (рис. 8,а) и противника (рис. 8, б) пострадали одинаково. У обеих потоплены линкор, один крейсер и один эсминец, продолжают сражение по одному крейсеру, по два эсминца и все четыре катера. Расположение наших кораблей противнику уже известно (на рис. 8,а они обведены пунктиром), и при своем ходе он разгромит их без промаха.

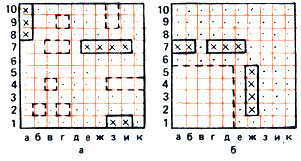
Рис. 8

К счастью, ход наш и судьба партии в наших руках. Мы должны потопить один за другим все семь его кораблей, сосредоточенных в квадрате 5*5. Для нахождения победной комбинации в этой напряженной схватке требуется прежде всего провести логический анализ ситуации.

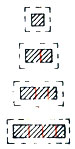
Рис. 9

По правилам любые два корабля отстоят друг от друга не меньше чем на одно поле. Окружим каждый корабль каймой шириной в полполя (рис. 9), полученный прямоугольник назовем достройкой этого корабля. Найдем теперь площадь достроек всех семи кораблей, которые предстоит поте пить. Достройка катера - 4 клетки (2*2), эсминца - 6 клеток (3*2) и крейсера - 8 клеток (4*2). Общая площадь достроек составляет 36 клеток. Но площадь достройки доски (доска с каймой в полполя) также 36 клеток, из чего следует, что угловые поля доски 5*5 обязательно заняты кораблями (иначе угловая площадь достройки доски "пропадает"). Переберем все возможные расположения кораблей. Их всего пять (рис. 10,а - д), повороты и зеркальные отражения доски не учитываются.

Рис. 10

Проведенный анализ позволяет эффектно завершить игру. Первые четыре выстрела следует произвести по углам доски 5*5. Как мы убедились, все они достигают цели. Если при этом три катера будут потоплены (рис. 10,а), то расположение остальных кораблей определяется однозначно. Пусть потоплен только один катер (рис. 10,6, в). Так как достройки кораблей плотно покрывают достройку доски, пятый и шестой выстрелы можно без риска произвести по полям аЗ и el, отстоящим на два поля от углового, занятого потопленным катером. От результатов этих двух выстрелов зависит, какой из случаев - "б" или "в" - имеет место. Если выстрелы по углам привели к потоплению двух катеров (рис. 10,г, д), то удары по полям аЗ и в5 позволят сразу выяснить, какой из двух вариантов избрал противник.

Итак, после шести выстрелов мы имеем полную информацию о расположении неприятельских кораблей и следующими пятью ударами победно завершим эту напряженную битву. Рассмотренный пример показывает, что в критической ситуации от играющих в морской бой требуется немалое искусство и выдержка.

Залпы выстрелов. До сих пор каждый выстрел производился по одному полю доски. Интересной разновидностью морского боя является игра, в которой один ход состоит сразу из ряда выстрелов - ведется, так сказать, массированный огонь по неприятельскому флоту. Соперник сообщает общие результаты стрельбы, не указывая при этом, в какой корабль и на каком поле произошло попадание. Например, при трех одновременных выстрелах ответы могут быть такими: три промаха; два промаха и одно попадание; один промах и одно потопление и т. д. (последний ответ означает, что два выстрела из трех попали в один и тот же корабль и потопили его). Остальные правила игры не меняются. После каждого хода и ответа на него игроки извлекают определенную информацию о дислокации неприятельских кораблей и следующими ходами пытаются использовать ее.

В другом варианте этой игры каждому игроку разрешается одновременно производить выстрелы по стольким полям доски, сколько у него еще осталось непотопленных кораблей. Обстреливаемый игрок вновь сообщает стреляющему только общее число попаданий, потоплений и промахов. При обычной флотилии из десяти кораблей первый ход состоит из десяти выстрелов. Если один или несколько кораблей потоплены, то число выстрелов уменьшается. Когда все корабли пойдут на дно, игрок л пишется права хода (0 выстрелов), но оно ему больше не нужно - бой закончился его поражением.

Рассмотрим еще одну интересную модификацию морского боя на произвольной квадратной доске. В ней также разрешается производить серии выстрелов. Будем считать, что флотилии обоих партнеров состоят из кораблей одного типа: катеров, эсминцев, крейсеров, линкоров или вообще кораблей k*1 (k-мино) на доске n*n (k≤n). Число к оговаривается до начала игры. Игрок может расставлять на доске любое количество кораблей, быть может, ни одного, не сообщая это число противнику.

Игра состоит всего из одного хода, который заключается в одновременном произведении выстрелов по ряду полей доски (залп выстрелов). При этом игрок получает информацию о каждом поле доски - попадание или промах (о потоплениях сообщений не делается). Проанализировав ответы противника, он должен однозначно определить расположение всей его флотилии. Победителем становится игрок, залп которого содержит меньше выстрелов.

Тестовой залп. Из трех рассмотренных нами тестовых игр (быки и коровы, отгадать слово, морской бой) ближе всего к математике лежит морской бой и его различные вариации. Теория тестов представляет собой один из современных разделов кибернетики, и ею занимаются многие математики. Под тестом понимается некоторый эксперимент, позволяющий получить полную информацию об анализируемом объекте. Поскольку эксперимент всегда требует определенных затрат на его проведение, необходимо, чтобы он был как можно проще, дешевле. В этом смысле описанные нами игры являются типично тестовыми. Далее, обсуждая последний вариант морского боя, мы для удобства воспользуемся "тестовой" терминологией.

По-прежнему будем называть множество выстрелов, которые одновременно производятся по полям доски, залпом. Если залп достигает цели - при любых ответах противника позволяет однозначно определить расположение всех его кораблей, мы называем его тестовым. Соответствующие выстрелы и поля, по которым они производятся, также будут тестовыми.

Описанная игра, хотя и является на редкость короткой (она длится всего один ход!), весьма оригинальна и необычна. Дело в том, что "слабый" залп, содержащий мало выстрелов, связан с риском, что мы не сможем однозначно определить расположение всех кораблей противника. В то же время при "сильном" залпе, когда число выстрелов велико и любой ответ противника гарантирует нам расшифровку всех его кораблей, есть риск, что мы просто-напросто проиграем по числу выстрелов в залпе. Кстати, в этой игре, как мы видим, очень важна очередь хода, поэтому играть надо одну партию "белыми" и одну - "черными".

Можно придать игре более строгий характер, исключив из нее элемент блефа. А именно потребуем, чтобы залп каждого игрока был тестовым, то есть обеспечивал однозначное распознавание всех кораблей противника при любом ответе. Далее мы будем рассматривать только такой вариант игры.

Очевидно, чтобы стать непобедимым в последнем варианте морского боя, достаточно для любых значений п и к решить следующую задачу.

По какому минимальному числу полей доски n*n следует произвести тестовый залп, чтобы при любых ответах противника можно было однозначно определить расположение всех его кораблей k*1 (а значит, и их число)?

Залп, который требуется найти в этой задаче, назовем минимальным тестовым залпом, а число тестовых выстрелов в нем обозначим через t(n, k).

Рассмотрим сначала простейший случай, когда игроки расставляют на своих досках только катера (k = 1). Очевидно, t(n, 1) = n². Если хотя бы одно поле доски не входит в тестовый залп, то при ответе "промах" на все тестовые выстрелы мы не сможем решить, находится катер на этом поле или нет.

Если к>1, то задача становится довольно сложной. Во всяком случае, автору известны решения только для крайних

случаев: k = 2 и k = n. В следующем пункте мы сформулируем их в виде двух отдельных задач.

Рис. 11

Минимальный тестовый залп.Задача 1. На доске n*n расположено некоторое количество эсминцев (кораблей 2*1), которым, как обычно, запрещено касаться друг друга. Каково наименьшее число полей, по которым надо выстрелить, чтобы после сообщения противником результатов залпа можно было однозначно определить расположение всех его эсминцев?

Решение этой задачи можно найти в книге И. Соловьева "Тесты", упомянутой в библиографии. Приближенный ответ такой: t(n, 2)≈ ⁴/₅ n², и, значит, минимальный тестовый залп должен быть произведен примерно по ⁴/₅ площади доски. Для обычной доски (10*10) ответ точный: t (10, 2) = ⁴/₅*10² = 80. Минимальный тестовый залп для этого случая приведен на рис. 11, причем тестовыми здесь являются все поля доски, кроме заштрихованных.

Задача 2. На доске n*n размещено некоторое количество кораблей n*1, которые не касаются друг друга. Каково минимальное число полей, по которым надо одновременно произвести выстрелы, чтобы после сообщения противником результатов этого залпа можно было однозначно определить расположение всех его кораблей?

Докажем, что для обычной доски 10*10 минимальный тестовый залп состоит из 14 выстрелов. Для этого достаточно установить, что во-первых, набор полей, отмеченных на рис. 12 крестиками, является тестовым и, во-вторых, что меньшим числом выстрелов не обойтись.

Рис. 12

Убедимся, что залп на рис. 12 тестовый. Рассмотрим последовательно, одну за другой, все горизонтали доски. Пусть по данной горизонтали произведены два выстрела. Если один из них или оба привели к промаху, то корабля на этой горизонтали нет. Если оба выстрела попали в цель, то горизонтальный корабль есть - в противном случае мы имели бы два вертикальных корабля с общей границей, что невозможно. Рассмотрим теперь горизонталь с одним тестовым полем. Если выстрел по нему дал промах, корабля на горизонтали нет. Если произошло попадание, то следует посмотреть на тестовое поле, соседнее с данным по вертикали. В случае промаха по нему корабль является горизонтальным, а при попадании - вертикальным. Таким образом, при любых ответах противника мы однозначно определяем расположение всех его кораблей 10*1 (их не больше пяти, причем только вертикальные или только горизонтальные).

Осталось показать, что наш тестовый залп минимальный. Предположим противное, пусть t (10, 10)≤13. Поскольку каждая горизонталь доски содержит хотя бы одно тестовое поле (иначе при всех промахах мы не сможем определить, занята данная горизонталь кораблем или нет), а всего таких полей не больше тринадцати, то минимум семь горизонталей содержат ровно одно тестовое поле; все эти поля назовем одинокими (по горизонтали). Кроме них, имеется не более 13-7 = 6 тестовых полей, занимающих максимум 6 вертикалей. Оставшиеся четыре вертикали (или больше) могут содержать только одинокие (по горизонтали) поля, причем не более семи. Это означает, что по меньшей мере одна вертикаль доски содержит ровно одно тестовое поле, причем оно является одиноким (по горизонтали).

Таким образом, мы нашли тестовое поле, одинаковое, как по горизонтали, так и по вертикали. Если тестовый залп приводит к попаданию в это поле и промаху по остальным, мы не сможем определить, какой именно корабль (горизонтальный или вертикальный) проходит через него. Итак, наш залп не является тестовым - противоречие.

В общем случае метод построения минимального тестового залпа для обнаружения кораблей n*1 вытекает из рис. 12. На три тестовых поля каждого из выделенных на нем квадратов 3*3 приходится еще по одному, четвертому (для доски 10*10 необходимо взять еще два поля в правом верхнем углу). Таким образом, имеем приближенную формулу 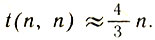Точный ответ зависит от остатка, который получится при делении n на 3 и компактно записывается следующим образом: 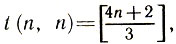Где квадратные скобки означают целую часть числа. Для n = 10 снова получаем t = 10.

Рис. 13

Последнюю задачу о минимальном тестовом залпе автор книги предложил для задачника "Кванта". Однако когда он раскрыл свежий номер журнала, то неожиданно обнаружил, что условие, по которому корабли не должны касаться друг друга, в тексте опущено, и получилась совсем другая задача! В частности, если вся доска заполнена кораблями, то никаким числом выстрелов невозможно распознать, какие n кораблей размещены на доске n*n - вертикальные или горизонтальные. Впрочем, если такое плотное расположение кораблей запретить, то новая задача имеет решение. Число выстрелов на этот раз придется увеличить - минимальный тестовый залп следует произвести по (2n-1) полям, например, так, как показано на рис. 13. Редактор задачника "Кванта" Н. Васильев, который "вынужден" был решать новую задачу, рожденную благодаря опечатке в журнале, попутно нашел и более эффектное решение первоначальной задачи - о кораблях, которые не должны касаться друг друга. Приведем его.

Пусть по-прежнему t = t (n, n) - число полей, по которым наносятся выстрелы минимального тестового залпа, через А обозначим само множество полей. Докажем, что 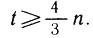Очевидно, каждая линия доски содержит хотя бы одно поле из А и на одной горизонтали или вертикали с ним имеется еще не меньше одного такого поля. Расставим на полях А синие и красные единицы и двойки следующим образом.

Если на горизонтали более одного поля из А, то поставим на каждом из них красную двойку. Проделаем такую же процедуру с вертикалями доски и запишем на полях А синие единицы и двойки. В результате на каждом поле А будут записаны либо единица с двойкой, либо две единицы, и, значит, сумма р всех написанных чисел не больше 3t. Поскольку на каждой линии доски мы записали "цветные" числа с суммой не меньше чем 2, то p≥4n. Итак, 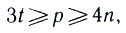откуда 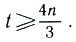Если n делится на 3, то точный ответ, как мы знаем, 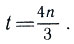Общая формула: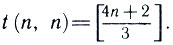

Вы, наверное, обратили внимание на то, что тестовый залп в последнем варианте морского боя анологичен стратегии в классической игре. Однако если стратегия гарантирует только попадание в единственный на доске корабль k*1, то тестовый залп позволяет однозначно определить расположение всей флотилии кораблей. Используя некоторую стратегию в обычном морском бое и попав в цель, нам остается только потопить корабль. Что же касается тестового залпа, то независимо от успеха отдельных выстрелов необходимо произвести их все до единого. Аналогом оптимальной стратегии служит минимальный тестовый залп. Желающие еще глубже развить теорию этой игры могут исследовать ее для других значений k, а именно 2<k<n.