Игры со словами

Рассмотренная нами в первой главе тестовая игра "отгадать слово" - одна из многих десятков известных словесных игр, хотя и выделяется среди них своими логическими и комбинаторными свойствами.

Игры со словами

Игры и развлечения со словами по своей популярности занимают одно из лидирующих мест среди других видов досуга. Кто из нас не увлекался в часы отдыха разгадыванием кроссвордов, чайнвордов, шарад, ребусов, криптограмм и других головоломок со словами?

Словесные игры расширяют эрудицию, развивают культуру речи и кругозор, учат работать со словарями. Немалое значение имеют они и для развития мышления и речи, поэтому часто используются воспитателями. Такие игры дают возможность не только потренировать память и проявить эрудицию, но и глубже проникнуть в тонкости языка, разобраться в структуре словообразования. Не случайно игры и развлечения со словами можно найти в замечательной "Книге о языке", принадлежащей перу известного американского популяризатора-филолога Ф. Фолсома.

Кроссворды. Читая эту главу, читатель, возможно, упрекнет автора в том, что некоторые словесные развлечения, в том числе, кроссворды, отнесены к играм, хотя их следовало бы назвать головоломками. Но это не всегда так, взять хотя бы "балду" - настоящая игра с несколькими участниками. Что же касается кроссворда... Вот сообщение, которое заставит отнестись к нему несколько иначе.

"Очередной чемпионат Великобритании по решению кроссвордов состоялся в Лондоне. В нем приняли участие 18 лучших специалистов со всех концов страны. Им было предложено поломать голову над четырьмя исключительно сложными заданиями. Первым с этой задачей справился Д. Сейкс, которому потребовалось всего 37,5 минуты, чтобы в шестой раз завоевать титул чемпиона Англии".

Заметим, что при составлении кроссвордов установлено немало забавных рекордов. Итальянец Г. Далмас придумал кроссворд, в котором насчитывается 52 тысячи клеточек. Его размер - 2*2,6 метра, общая площадь более 5 квадратных метров. Всего в кроссворде 12 тысяч слов, самое большое состоит из двадцати одной буквы. Кроссворд французов Ж. Луизе и Г. Брути содержит 50 тысяч квадратиков, образующих гигантскую геометрическую фигуру, и 18 тысяч слов. Наконец, рекордный кроссворд Р. Букаэрта включает в себя 25 283 слова, он заполняет ленту длиною 12 метров. Рекордсмен создавал свое детище в течение четырех лет. Интересно, нашелся ли хоть один смельчак, который взялся за его разгадку?

Наборщик. Это одна из самых распространенных игр. Берется произвольное слово и из его букв составляются (набираются) другие слова. Как обычно, используются только имена существительные, нарицательные в исходной форме, в единственном числе, в именительном падеже и никаких ласкательно-уменьшительных. Выигрывает тот, у кого окажется больше слов. Впрочем, часто учитывают и оригинальность слов, количество букв в них. Например, если играют четверо, слово, найденное одним участником, оценивается в 3 очка, двумя - 2 очка, тремя - 1 очко, а если оно записано всеми, то просто вычеркивается (0 очков).

От играющих в "наборщика", помимо эрудиции и большого запаса слов, требуются комбинаторные навыки - ведь приходится производить немалый перебор букв и слов. Может быть, поэтому в соревнованиях между "физиками и лириками" первые побеждают чаще...

Мастера словесных игр знают много важных секретов, и одно из их основных оружий - анаграммы. Как уже говорилось в первой главе, слово, составленное из всех букв данного слова, называется его анаграммой. Два или более слов, образованных из одних и тех же букв, дают блок анаграмм.

Приведем несколько примеров: КОЛБА - БОКАЛ - блок из двух пятибуквенных анаграмм: ПРИКАЗ - КАПРИЗ - блок из двух шестибуквенных анаграмм; КАРТА - КАРАТ - КАТАР - блок из трех пятибуквенных анаграмм; КЛОУН - КОЛУН - УКЛОН - КУЛОН - блок из четырех пятибуквенных анаграмм.

Разумеется, опытные игроки, обнаружив одно слово из блока анаграмм, не задумываясь, выписывают и все остальные, чем немало удивляют неискушенных "наборщиков".

ЭВМ и анаграммы. Составление анаграмм само по себе интересная словесная игра. Здесь имеется немало вопросов, на которые пока не найдено ответов. Не известно, например, сколько всего в русском языке анаграмм, сколько блоков, содержащих то или иное количество слов, и т. д. "Теория" анаграмм заинтересовала программистов, создателей программы "Каисса" - первой чемпионки мира по шахматам среди ЭВМ. Однажды, когда "Каисса" была на отдыхе, ее авторы решили написать программу для "вычисления" анаграмм. В память ЭВМ был введен (не в полном объеме) 4-томный "Толковый словарь русского языка" Д. Ушакова. Прочитав его, компьютер обнаружил около 1000 анаграмм и попутно установил ряд любопытных рекордов.

И раньше были известны анаграммы с числом букв, большим шести. Вот несколько красивых примеров: МАТЕРИК - МЕТРИКА, МОШКАРА - РОМАШКА, РОТОНДА - ТОРНАДО (7 букв); АПЕЛЬСИН - СПАНИЕЛЬ, НОРМАТИВ - МИНОТАВР, ХОРИСТКА - АКРОСТИХ (8 букв); ВЕРТИКАЛЬ - КИЛЬВАТЕР, ГЕОМЕТРИЯ - ГЕОТЕРМИЯ, СТАЦИОНАР - СОРАТНИЦА (9 букв); МОНОГРАММА - НОМОГРАММА, ГРАФОЛОГИЯ - ГОЛОГРАФИЯ, ДОЗРЕВАНИЕ - РАЗДВОЕНИЕ (10 букв).

Машине удалось продвинуться дальше. Сначала она увеличила рекорд на одну букву: РАТИФИКАЦИЯ - ТАРИФИКАЦИЯ, а затем довела его до пятнадцати букв: СТАРОРЕЖИМНОСТЬ - НЕРАСТОРЖИМОСТЬ!

Как ЭВМ находит анаграммы? Конечно, если брать одно слово за другим и в каждом из них переставлять буквы всеми возможными способами, это будет долгая и кропотливая работа даже для мощного компьютера. Алгоритм, которым пользовалась ЭВМ, заключается в следующем. Сначала весь введенный в нее словарь переводится на другой "язык", в каждом слове которого буквы расположены в алфавитном порядке. Например, КОРШУН теперь читается как КНОРУШ, и в это же буквосочетание превращается ШНУРОК. Полученные "словарь" уже сам записывается в алфавитном порядке, и, очевидно, набор одинаковых слов, расположенных в нем по соседству, дает нам некоторый блок анаграмм в настоящем словаре. Так, обнаружив в новом "языке" два раза подряд слово КНОРУШ, обратным переводом мы найдем блок анаграмм ШНУРОК - КОРШУН.

Компьютер увлекся и другими словесными играми, установив несколько оригинальных рекордов. Из какого наибольшего числа различных букв может состоять слово? Машина написала два слова из 14 букв: ЗВУКОСНИМАТЕЛЬ и РАЗГИЛЬДЯЙСТВО.

Два самых длинных слова, в которых гласные чередуются с согласными, по мнению компьютера, также содержат по 14 букв: ВЕЛИКОМУЧЕНИЦА и СОЛОМОВОЛОКУША. Конечно, эти рекорды нельзя считать абсолютными, так как был исследован лишь один словарь, да и тот не в полном объеме. Если ввести в ЭВМ какой-нибудь другой словарь (Даля, Ожегова и т. д.) или энциклопедию, то, возможно, будут установлены новые рекорды в тех или иных словесных играх.

Вернемся к анаграммам. Как мы знаем, рекордный блок пятибуквенных анаграмм содержит шесть слов: АВТОР - ВТОРА - ОТВАР - РВОТА - ТАВРО - ТОВАР. Он часто встречается в "наборщике", получается, скажем, из слова ЛЕКАРСТВО. Это весьма плодотворное для игры слово содержит и другие блоки анаграмм, например стандартный набор из четырех слов: РОСТ - СОРТ - ТОРС - ТРОС, а также красивые шестибуквенные анаграммы: ВЕКТОР - КОРВЕТ, КОРСЕТ - СЕКТОР. Замечу, кстати, что один мастер игры в "наборщика" превратил ЛЕКАРСТВО в 180 слов. Попробуйте побить этот рекорд.

Открытые еще в III веке до нашей эры греческим грамматиком и поэтом Ликофроном анаграммы до сих пор привлекают внимание языковедов, поэтов и просто любителей словесных развлечений. Коллекция В. Капранова насчитывает 526 анаграмм, использующих 1119 слов. Выше мы привели анаграммы, содержащие число букв от 4 до 11 и 15 (рекорд). Приведем интересные примеры с "промежуточным" числом букв: ВЫБОРОЧНОСТЬ - ОБРЫВОЧНОСТЬ, УТОНЧЕННОСТЬ - УТОЧНЕННОСТЬ (12 букв), ПЕРЕМАЛЫВАНИЕ - ПЕРЕЛАМЫВАНИЕ (13 букв), ОГРАНИЧЕННОСТЬ - НЕОРГАНИЧНОСТЬ (14 букв).

Если отойти от канонических правил и не связывать себя грамматическими рамками, можно придумать множество самых необычных анаграмм. Приведем наиболее забавные примеры: СХЕМА СМЕХА, ФИАЛКА КАЛИФА, УЖИМКА МУЖИКА, РЕКЛАМА МАКЛЕРА, ЦИТАТА ТАЦИТА, ЗАПОНКА НАПОКАЗ, АПОСТОЛ ПОЛОСАТ, ВОЛОКИТА КИТОЛОВА.

Газета "Советская Россия" часто проводит различные словесные конкурсы, инициатором которых выступает М. Крушинский. В одном из них подлинным виртуозом игры в анаграммы показал себя Д. Авалиани, составивший целые фразы из анаграмм. Вот некоторые из его открытий: ВИЖУ ЗВЕРЕЙ - ЖИВУ РЕЗВЕЙ; ИНОК ВЯЗНЕТ, КОНИ ЗВЕНЯТ; УВИДИМСЯ - УДИВИМСЯ, ОТ-СПОРИМСЯ -ОПРОСТИМСЯ; СЛЕПО ТОПЧУТ - ПОСЛЕ ПОЧТУТ.

Палиндромы. Перевертыши, или палиндромы,- это слова, которые читаются одинаково слева направо и справа налево: ПОП, ДОВОД, ДОХОД, ПОТОП, ТОПОТ, НАГАН, ЗАКАЗ, КАЗАК, ШАЛАШ. Многие любители словесных развлечений увлекаются.составлением предложений, а то и маленьких рассказов или стихов, которые одинаково читаются в обе стороны. Вот несколько смешных фраз-палиндромов: "Аргентина манит негра", "Торт с кофе не фокстрот", "И любит Сева вестибюли", "Удавы рвали лавры в аду", "Я и ты будем в меду бытия", "Я не мил - и не женили меня", "Укроп наворован? Порку! А ремень - не мера", "Лилипут сома на мосту пилил", "Ах, у печали мерило, но лире мила чепуха!" А вот двустишие Д. Авалиани, в котором безупречный гомеровский гекзаметр сочетается с прямым обращением к великому эллину:

"Море могуче. В тон ему,
шумен, отвечу Гомером:
Море, веру буди - ярок,
скор, я иду буревером..."

Палиндромы придумывали многие поэты. Забавный перевертыш "А роза упала на лапу Азора" принадлежит великому русскому поэту А. Фету, другой знаменитый поэт Г. Державин сказал: "Я иду с мечом, судия", а замечательный русский поэт В. Хлебников, кстати, увлекавшийся математикой, написал целое стихотворение "Перевертень", где все строчки можно прочитать в обратном порядке.

Каркас. Известна старинная головоломка, в которой надо найти набор слов, использующий все 33 буквы алфавита, причем по одному разу каждую. Вот набор из девяти слов: БЫК, ВЯЗ, ГНОЙ, ДИЧЬ, ПЛЮЩ, СЪЕМ, ЦЕХ, ШУРФ, ЭТАЖ. Существует ли набор, состоящий из меньшего числа слов, не известно. Задаче можно придать более увлекательную форму, если потребовать, чтобы слова образовали осмысленную фразу.

Интересную игру на составление слов - "каркас" придумал один из создателей "Каиссы" и автор машинной программы поиска анаграмм А. Битман.

Играющие фиксируют несколько согласных, а гласные (а также й, ь, ъ) подбирают произвольно, в любом количестве. Иначе говоря, составленные слова натягиваются на каркас из данных согласных букв (при этом должен быть использован весь набор согласных, которые можно переставлять в любом порядке). Пусть, например, выбраны буквы К, Н, Т. Тогда нас устраивают такие слова: КАНТ, ТАНК, КНУТ, КАНАТ, НАКАТ, ТКАНЬ, ТОНИКА, НЫТИК, ОКТАН, НИТКА и т. д. Побеждает тот, кто натянет на каркас больше слов.

В основе игры, по мнению ее изобретателя, лежит свойство согласных как бы образовывать скелет слова. Если вычеркнуть из текста все гласные (но разумеется, не менять порядок согласных), часто его смысл может быть восстановлен. Так, изречение "Волга впадает в Каспийское море" легко прочесть и в сокращенном виде: "Влг впдт в Кспск мр".

В русском языке нет существительных, состоящих только из гласных. Но уже с одной согласной можно успешно играть в "каркас". Например, на букву Л натягиваются слова: АЛОЭ, АУЛ, ЕЛЕЙ, ЕЛЬ, ИЛ, ИЮЛЬ, ЛЕЯ, ЛЬЕ, УЛЕЙ, ЭЛЬ, ЮЛА, ЯЛ. Если использовать Л больше одного раза, число слов возрастает: АЛЛЕЯ, ЛИЛИЯ и т. д.

Чтобы игра протекала веселее, Ю. Фокин предложил придумывать фразы, используя всякий раз только одну согласную, например: "Бобби, убей боя и бей бабу у баобаба", "Алло! Элла, у Аллы лилия алая? А у Лили алоэ?" "У Юры аэрарий - рай!"

Метаграммы и цепочки слов. Какие еще развлечения со словами пользуются популярностью? О кроссворде уже шла речь выше. Его младший брат - чайнворд, в нем словаре пересекаются, а располагаются друг за другом - конец предыдущего служит началом следующего. В ребусах нужно отгадывать слова или фразы, которые изображаются комбинацией условных значков, фигур, цифр. В шарадах слова разбиваются на части, имеющие самостоятельное значение (виноград = вино + град). Арифмогриф и криптограмма - это задачи на отгадывание слов или текстов, где буквы зашифрованы цифрами. Словарный запас и быстроту реакции развивают игры, в которых надо придумывать рифмы, синонимы, антонимы или омонимы.

Большая изобретательность требуется в игре "цепочки слов", основанной на словах-метаграммах. Метаграмма данного слова получается заменой одной из его букв на другую. Игра заключается в нахождении цепочки метаграмм, соединяющей два заданных слова. Так, КОЗА за разное число ходов превращается в других животных: КОЗА - ПОЗА - ПОЛА - ПОЛК - ВОЛК; КОЗА - ЛОЗА - ЛУЗА - ЛУПА - ЛИПА - ЛИСА; КОЗА - КОРА - КАРА - ФАРА - ФАРС - БАРС.

Как мы видим, каждое слово цепочки получается из предыдущего заменой ровно одной буквы. Выигрывает тот, чья цепочка короче. Изобрел эту увлекательную игру Л. Кэролл, автор "Алисы в стране чудес" и один из классиков занимательной матиматики.

Для тренировки можно играть и в более простую игру, соревнуясь в количестве метаграмм для того или иного слова. Так, ДОМ порождает девять метаграмм: КОМ, ЛОМ, РОМ, СОМ, ТОМ, ДЫМ, ДОГ, ДОК, ДОЛ. А слово КОЧКА дает целых 11 метаграмм: БОЧКА, ДОЧКА, МОЧКА, НОЧКА, ПОЧКА, ТОЧКА, КАЧКА, КИЧКА, КУЧКА, КОРКА, КОШКА.

Каков рекорд числа метаграмм, образованных из одного слова, не известно.

При нахождении цепочек метаграмм интересны такие пары исходных слов, которые представляют собой антонимы или какие-нибудь противопоставления. В самых популярных цепочках МУХА превращается в СЛОНА. Вот одна из них, где цель достигается за 16 ходов: МУХА - МУРА - ТУРА - ТАРА - КАРА - КАРЕ - КАФЕ - КАФР - КАЮР - КАЮК - КРЮК - УРЮК - УРОК - СРОК - СТОК - СТОН - СЛОН. Кто придумает цепочку короче?

На ход позднее НОЧЬ "меняется" на ДЕНЬ, за 11 ходов РЕКА "впадает" в МОРЕ и за 13 ходов, если есть ТЕСТО, получается БУЛКА. Попробуйте улучшить.и эти рекорды.

Интересны и многократные превращения. В следующей цепочке МИГ дает ЧАС, который, в свою очередь, переходит в ГОД, затем возникает ВЕК и в конце концов наступает ЭРА. Это удивительное путешествие во времени занимает 17 ходов: МИГ - МАГ - МАЙ - ЧАЙ - ЧАС - ЧАД - ГАД - ГОД - ГИД - ВИД - ВИС - ВЕС - ВЕК - БЕК - БОК - БОА - БРА - ЭРА. Конечно, если не ставить промежуточные цели, переход можно осуществить быстрее (за 6 ходов) МИГ - МИР - МОР - БОР - БОА - БРА - ЭРА.

Устраивать состязания, у кого короче цепочка метаграмм, не столь интересно, если заранее не знать, существует ли хоть одна из них. А ведь даже многие короткие слова не имеют метаграмм, о цепочках и говорить не приходится. М. Гервер предложил более увлекательные правила игры в "цепочки слов". На каждом шагу вновь меняется одна буква слова, но теперь разрешается также произвольно менять порядок всех букв.

Сложность образования метаграмм состоит в преобразовании гласных в согласные и наоборот. Вот почему так долго МУХА превращалась в СЛОНА. На месте двух гласных появились согласные, а одна согласная сменилась гласной. При новых правилах такой проблемы не возникает. Автор модифицированной игры в "цепочки слов" сделал из МУХИ СЛОНА всего за пять ходов, а из КОЗЫ ВОЛКА за три: МУХА - ХУЛА - ЛУНА - ЛУНЬ - НОЛЬ - СЛОН; КОЗА - КОСА - ВОСК - ВОЛК.

Вторая цепочка, очевидно, является рекордной, так как три новые буквы быстрее чем за три хода появиться не могут. В классическом превращении МУХА - СЛОН слова состоят из разных букв, и поэтому можно надеяться на цепочку из четырех переходов, но не меньше...

Здесь автор позволит себе небольшое отступление. После выхода в свет первого издания книги я получил от читателей множество писем, в которых обсуждались различные игры, предлагались новые, уточнялись те или иные решения, устанавливались рекорды. Очевидно, наиболее интересные соображения читателей были учтены при работе над вторым изданием. Что касается последней игры, Ю. Фокиным был установлен абсолютный рекорд: МУХА - ХЛАМ -ХОЛМ - СЛОМ - СЛОН, причем из цепочки исключено числительное НОЛЬ.

Ассоциации. Идее игры в "цепочки слов" можно придать несколько иной вид. Два слова или понятия будем считать ассоциативно связанными, если между ними есть что-то общее - смысловая, логическая или какая-то иная связь. В игре "ассоциации" требуется найти кратчайшую цепочку ассоциативных переходов между двумя данными словами.

Два весьма отдаленных понятия иногда удается связать между собой всего за несколько переходов. Возьмем, к примеру, слова НЕБО и ЧАЙ. Следующая последовательность ассоциаций решает задачу за четыре шага: НЕБО - ЗЕМЛЯ - ВОДА - ПИТЬЕ - ЧАЙ. В данном ряду слов ассоциативность соседей не вызывает сомнения. Но ассоциация, конечно, не столь точное понятие, как метаграмма, и поэтому в игре не исключены споры, которые лучше всего решать голосованием.

Любопытно, что ассоциативные переходы слов исследовались психологами, в частности, построение различных ассоциативных цепочек моделировалось на ЭВМ. Количество переходов в цепочке может служить мерой "смыслового расстояния" между двумя понятиями. Многочисленные опыты, проведенные учеными, позволили выдвинуть неожиданную гипотезу: для любых двух слов (понятий) существует ассоциативная цепочка, состоящая не более чем из семи слов. Иначе говоря, два произвольных понятия, даже весьма отдаленные друг от друга, имеют тесную связь - смысловое расстояние между ними составляет не более шести шагов.

Балда. В этой, пожалуй, самой популярной словесной игре можно обойтись даже без карандаша и бумаги, а играть, как говорят шахматисты, вслепую. Первый игрок называет произвольную букву, второй добавляет букву слева или справа, имея в виду некоторое слово. Следующий игрок (или снова первый, если играют двое) также приписывает букву с одной из сторон, имея в виду свое слово, и т. д. Тот, кто очередным ходом вынужден закончить слово, либо вообще не может приписать никакой буквы (потому что не догадывается, как уже написанные буквы продолжить до слова), проигрывает кон и в наказание получает "б". При вторичном проигрыше "б" превращается в "ба", затем в "бал", и в конце концов кто-то первым становится балдой.

Хотя, рассказывая об игре "отгадать слово", мы несколько снисходительно отозвались о "балде", в некоторых ситуациях более удачного словесного развлечения не придумаешь. Когда я прогуливаюсь по лесу со своим маленьким сыном и он говорит: "Папа, сыграем во что-нибудь", ничего более подходящего, чем "балда", в голову не приходит,- игра в "города" исчерпывается слишком быстро.

На первый взгляд занятие это бесхитростное, но и в "балде" есть свои мастера. А иногда искусство игры приобретает решающее значение... В книге М. Мироновой и А. Менакера "В своем репертуаре" Александр Семенович рассказывает о том, как страстно увлекались "балдой" в довоенные годы артисты Театра эстрады и миниатюр. Шутили тогда, что все они просто обалдели. Порой актеры так заигрывались, что опаздывали на сцену. Когда Менакер впервые попал в театр, его больше всего поразила удивительная находчивость Марии Владимировны, которая никогда не проигрывала в "балду" (только Рина Зеленая могла с ней соревноваться). Попытка раскрыть секрет ее непобедимости привела в конце концов к созданию замечательного семейного и эстрадного дуэта!

Буквы в игре принято приписывать с краю, хотя ничто не мешает вставлять их и внутрь "полуфабриката". Кстати, именно так играют в "антибалду". В этой игре все наоборот - каждый из двух участников стремится закончить слово, причем сделать это как можно большее число раз. В тот момент, когда противники не видят продолжения последнего слова, игра прерывается и идет подсчет очков.

Вернемся к нормальной "балде". Игра эта словесная, но присутствие в ней комбинаторных и логических элементов не вызывает сомнения. Не случайно известный советский математик, покойный профессор Г. Шилов и математик В. Берман увлекались игрой и написали о ней целое исследование.

Мастера игры умеют выкручиваться из самых трудных ситуаций. Вместо того чтобы закончить слово, намеченное партнером, они находят неожиданный ход, к слову добавляется приставка или суффикс, и оно меняет свое "направление".

Большую роль играет знание выигрывающих буквосочетаний. Пусть, например, вы начали игру буквой Б, а ваш партнер мгновенно ответил БШ. Вы мучительно ищете слово, в котором рядом стоят буквы Б и Ш, а он такое слово, да еще заканчивающееся на вас, знает заранее - ОБШИВКА.

Шилов и Берман ввели термин "разрешимое двубуквенное сочетание" - пара букв, которую можно дополнить до некоторого слова. В качестве примера они привели партию, состоящую всего из двух ходов.

1-й игрок: Г; 2-й игрок ГЗ (имея в виду ЗИГЗАГ); 1-й игрок сдался, так как не нашел продолжения.

Этот пример показывает, как важно владеть набором разрешимых сочетаний. Из 33 букв алфавита составляется 332=1089 пар, но многие из них неразрешимы по правилам русского языка - ГЙ, ОБ, ЖЫ и т. д. Авторы введенного термина обнаружили 801 "разрешение", а также составили список двубуквенных сочетаний, для которых пока не найдены допустимые слова. >

Вопрос о существовании "разрешений" имеет скорее теоретический интерес. Так, если бы в приведенном примере первый игрок "вычислил" слово ЗИГЗАГ, он бы выиграл партию, потому что оно заканчивается на втором игроке. Даже если допустимое слово устраивает нас, не исключен риск, что найдется другое слово, которое мы будем вынуждены закончить. Иное дело, если двубуквенное сочетание имеет единственное разрешение. Убедившись, что это слово безопасно для нас, можно смело называть вторую букву пары - победа гарантирована. Конечно, установить единственность разрешения еще сложнее, чем его существование.

Королевская балда. Обычная игра в балду допускает различные обобщения. Об одном из них - антибалде - мы уже упоминали. Иногда играют, приписывая буквы не только слева и справа, но и сверху, снизу, по диагонали и т. д. Если традиционная игра как бы линейна, то теперь получается плоский вариант. Интересную разновидность такой игры Э. Иодковский предложил назвать королевской балдой.

В квадрате 5*5 по средней горизонтали записывается произвольное пятибуквенное слово. Далее игроки по очереди вписывают по одной букве в любую пустую клетку "доски", соседнюю с одной или несколькими клетками (полями), где уже есть буквы. Из написанных букв (не обязательно всех) должно образовываться новое слово, которое читается как серия ходов шахматного короля по доске. Цепочка букв, из которых складывается слово, является неразрывной и несамопересекающейся, то есть одну и ту же клетку король не должен проходить дважды. За каждую букву образованного на данном ходу слова начисляется очко. После составления двадцати слов (число свободных клеток доски) игра заканчивается и ведется подсчет очков.

В этой игре от простой "балды" взят основной принцип - добавления одной буквы, а от шахмат - образование слов ходом короля. Забавный гибрид шахматной игры и словесной!

Играть в королевскую балду можно вдвоем, вчетвером или впятером, так как число 20 делится без остатка на 2, 4, 5, и, значит, у соперников будет поровну слов. Для игры втроем квадрат должен быть побольше - 6*6, а первоначальное слово шестибуквенным, в этом случае у каждого участника на финише будет по 10 слов. Разумеется, для победы на каждом ходу следует придумывать слова подлиннее, используя как можно больше ранее записанных букв.

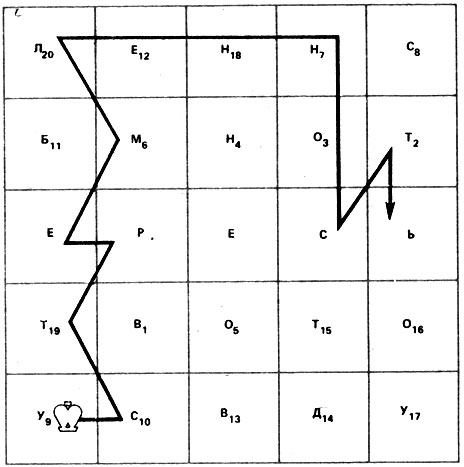
Рис. 14

В отличие от обычной в королевскую балду интересно играть и одному. Задача состоит в том, чтобы, приписывая букву за буквой, набрать как можно больше очков Рекордная "партия" показана на рис. 14. Исходное слово "ересь", номера ходов указаны на полях квадрата. Вот те 20 слов, которые появляются в процессе игры (выделены буквы, добавленные при образовании этих слов):

1. Север. 2. Весть. 3. Отсев. 4. Верность. 5. Соверен. 6. Мерность. 7. Временность. 8. Современность. 9. Уверенность. 10. Суверенность. 11. Бренность. 12. Беременность. 13. Своевременность. 14. Доверенность. 15. Тостер. 16. Достоверность. 17. Удостоверенность. 18. Осовремененность. 19. Мертвенность. 20. Устремленность.

Итого 210 очков, полученных в результате сложения длин всех слов. Немало пришлось королю потрудиться, побродить по доске, чтобы набрать эту .сумму. На рисунке изображен его последний маршрут, сделанный на 20-м ходу. Как мы видим, образованное слово (как, очевидно, и все предыдущие) отвечает всем необходимым условиям.

Словесное лото. В наш бурный век, когда времени для общения остается так мало, классическое числовое лото можно рекомендовать как хорошее средство для дружеских встреч. Заполняя, не торопясь, числовые карточки бочонками лото, можно обсудить какой-нибудь интересный вопрос, как это делали герои чеховских пьес. Но как интеллектуальное занятие лото не самый лучший объект, здесь не надо напрягаться, ломать голову. Другое дело, словесное лото. Как и в королевской балде, на листе бумаги рисуется квадрат, например 6*6. В процессе игры его клетки заполняются буквами так, чтобы при чтении по вертикали и горизонтали можно было прочитать побольше слов. При своем ходе игрок произносит любую букву, и все участники записывают ее в пустые клетки квадрата. Игра продолжается до заполнения всего квадрата, после чего подсчитываются очки. Чтобы поощрить более длинные слова, можно ввести такую шкалу: за слово из шести букв начислять 20 очков, из пяти - 10, из четырех - 5, из трех - 2 очка. Двубуквенные слова и слова, являющиеся частями более длинных слов, не учитываются.

Эрудит. Игра "эрудит" - ее предшественник американский "скрэбл" - пожалуй, одна из самых интересных игр в слова, сочетающая в себе логические и комбинаторные моменты с элементами кроссворда и даже домино.

Игра ведется на доске 15*15. "Базар" содержит 131 фишку, на которых изображены буквы и оценивающие их числа. Как и в домино, каждый игрок берет по семь фишек и держит их в тайне от партнеров. За один ход можно составить несколько слов из фишек, имеющихся на руках и расположенных на доске. Новое слово нельзя образовывать без завязки со старыми, то есть оно должно получаться из написанного слова плюс одна или несколько новых букв. Таким образом, все слова пересекаются, как в кроссворде. После сделанного хода игрок, как в домино, дополняет из базара свой запас фишек до семи.

За каждое новое слово начисляется столько очков, сколько записано на буквах, входящих в его состав. На доске имеется ряд цветных полей, которые меняют оценку. Очки буквы, занимающей зеленое поле, удваиваются, желтое - утраиваются. Если одна из букв на синем поле, удваивается сумма очков всего слова, а если на красном - утраивается. Игра продолжается либо до определенного числа очков, например 200, либо до полного опустошения базара. Мы не приводим здесь рисунка разукрашенной доски, потому что комплект игры продается в магазинах игрушек, и вряд ли вы будете делать доску и фишки самостоятельно.

Любопытно, что при разработке "эрудита" не обошлось без математического вмешательства! При решении вопросов о том, сколько фишек с той или иной буквой должно быть на базаре и какие цены назначить буквам, необходимо было провести частотный анализ русского языка. Материалом для такого исследования служат различные тексты, на основании вторых судят о частоте повторяемости отдельных букв. Существует много работ на этуктему, даже созданы специальные частотные словари. Однако воспользоваться ими для "эрудита" не так просто. Ведь помимо частоты букв, надо учитывать их положение в слове - одни буквы чаще встречаются в начале слов, другие - в конце. Кроме того, у нас допускаются лишь существительные в единственном числе именительном падеже. Распределение же букв в них отличается от распределения букв в других частях речи, которыми не рарешается пользоваться в игре. Все эти нюансы были учтены при создании "эрудита".