1.5.1. Cпособы задания топологии

Задать топологическое пространство - значит задать носитель Х и топологию τ, то есть указать те подмножества Х, которые будем считать открытыми.

Примеры.

1. Произвольное множество X можно сделать топологическим пространством, если называть открытыми все его подмножества, то есть на любом X включим в топологию вообще все подмножества X (в том числе и все его точки, то есть одноточечные подмножества), само X и пустое подмножество. Такая топология называется дискретной: τ = {X,∅, 2^X}, где 2^X - все подмножества множества Х.
2. Второй крайний случай - антидискретная (тривиальная) топология или топология слипшихся точек: на любом носителе X рассмотрим топологию, в которой всего два множества: все X и пустое: τ = {X,∅}.
3. Вещественная прямая R является топологическим пространством, если назвать открытыми множествами произвольные (пустые, конечные или бесконечные) объединения конечных или бесконечных интервалов. Действительно, вся числовая прямая очевидным образом открыта, пустое множество включают в число открытых по определению (это непротиворечиво, поскольку в пустом множестве нет точек, тогда можно считать, что каждая из них (!) входит в пустое множество с некоторой ε-окрестностью). Топологию, состоящую из обычных открытых множеств на числовой прямой, называют нормальной (обычной) топологией. Точно также строится нормальная топология в Rⁿ. Таким образом, нормальная топология - это топология стандартных метрических пространств.
4. Топология Зарисского на числовой прямой. В эту топологию включены вся прямая, пустое множество и все множества на прямой, дополнения которых до R состоят из конечного числа точек. То есть открытые интервалы получены выбрасыванием из прямой конечного числа точек.
5. Правая стрелка R _→. Эта топология на числовой прямой состоит из всей прямой, пустого множества и всех открытых интервалов вида (a,+∞), где a - точка прямой. Аналогично можно задать и левую стрелку.
6. X = {a,b} - топологическое двоеточие. Дискретная топология: τ₁ = {X,∅,{a},{b}}, антидискретная топология: τ₂ = {X,∅}. На двоеточии возможны ещё две топологии: τ₃ = {X,∅,{a}} и τ₄ = {X,∅,{b}}. Метризуема (то есть можно ввести расстояние) только дискретная топология: 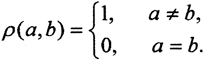Остальные - нет. В случае, например, τ₄ = {X,∅,{b}} открыты следующие множества: X = {a,b}, пустое множество ∅ и {b}, замкнуты X = {a,b}, пустое множество ∅ и {a}.