I. Пространства носителей

1.1. Линейная структура

Определение 1.Линейной структурой L (линейным пространством, векторным пространством) называют абелеву аддитивную группу (её элементы x∈L называют векторами), определённую над полем произвольной природы (элементы поля называют скалярами α,β,..λ...), причём αx∈L, а естественное согласование между группой и полем обеспечивается аксиомами дистрибутивности: λ(x+y)=λx+λy, (λ+μ)x=λx+μx, ассоциативности по элементам поля (λμ)x=λ(μx) и унитарности 1*x=x. (Символом 1 обозначен нейтральный элемент поля по умножению). Поле вещественных чисел R и поле комплексных чисел C называют основными полями, полагая, что поле R стандартно вложено в поле C. Если основное поле любое, то его обозначают буквой F. То есть линейная структура - это четвёрка (L, F, +, ·).

Комментарий. (Для краткости обычно вместо (L, F, +, ·) говорят L. Если абелева аддитивная группа определена над любым кольцом, то такая структура называется модулем. Иногда под векторным пространством понимают абелеву аддитивную группу, определённую над телом.)

Примеры групп. Примерами групп являются целые, рациональные, действительные, комплексные числа по сложению, ненулевые рациональные, действительные, комплексные числа по умножению. Все эти группы являются абелевыми. Следующий пример групп возникает из векторных пространств. Пусть L - векторное пространство над полем F. Множество невырожденных линейных преобразований векторного пространства L образует группу. Легко проверить, что векторные пространства одинаковой размерности n над одним и тем же полем изоморфны пространству строк длины n, а множество невырожденных линейных преобразований изоморфно множеству невырожденных матриц при обычном понимании сложения и умножения на число.

Примеры линейных структур.

• Два тривиальных пространства: вещественные числа над полем вещественных чисел и нулевое пространство, состоящее из одного нулевого элемента.
• Вещественные числа над телом рациональных чисел; вещественные числа над полем комплексных чисел не образуют векторное пространство (умножение комплексного числа на действительное есть число комплексное).
• Комплексные числа над полем вещественных чисел.
• Полиномы с степени не выше чем n над полем вещественных чисел с обычными операциями сложения и умножения на число.
• Множество конечномерных линейных операторов над полем вещественных чисел с обычными операциями сложения и умножения на число.
• Множество квадратных матриц над полем вещественных чисел с обычными операциями сложения и умножения на число.
• Множество геометрических векторов на плоскости или в 3-мерном пространстве с обычным понятием равенства (совпадение при параллельном переносе) и обычными операциями сложения векторов и умножением вектора на число.
• Множество, состоящее из всевозможных упорядоченных наборов из n чисел, действительных или комплексных с обычными операциями сложения и умножения наборов на число.
• Множество всех непрерывных на заданном промежутке [a,b] функций. Это пространство можно рассматривать как линейное, если определить сумму элементов и умножение на вещественное число обычным образом. Нулевым элементом этого пространства является функция, тождественно равная нулю.
• Последовательности {x_n} вещественных чисел над полем вещественных чисел с обычными операциями сложения и умножения на число, удовлетворяющие условию .
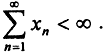• Расширение поля как линейное пространство. Пусть поле F включено в поле G, то есть F⊂G. Тогда поле G можно рассматривать как линейное пространство над полем F, так как ∀λ∈F и ∀x∈G определено произведение λx по определению поля G, а все аксиомы линейного пространства над полем F выполнены, так как это аксиомы поля G.

Комментарий. (Для произвольного линейного пространства L, как и для знакомого из линейной алгебры пространства Rⁿ, можно ввести понятие линейной зависимости и независимости системы векторов линейного пространства L и, соответственно, понятие о размерности линейного пространства L. Достаточно вместо векторов из пространства Rⁿ говорить о векторах из линейного пространства L.)

Определение 2.Линейное пространство L называют бесконечномерным, если для любого натурального числа N в нём имеется система из N штук линейно независимых векторов.

Пример. 1. Покажем, что бесконечномерным является линейное пространство всех непрерывных (как и интегрируемых) на сегменте [0,1] функций.

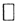
1. В силу определения 2 достаточно доказать, что на сегменте [0,1] существует любое целое положительное число линейно-независимых элементов. Покажем, что функции 1,x,x²,...,xⁿ, принадлежащие этому пространству, и образуют систему линейно-независимых векторов для любых n∈N. Действительно, возьмём произвольные вещественного числа γ₁,γ₂,...γ_n, и составим линейную комбинацию γ₀*1+γ₁*x+γ₂*x²+...+γ_n*xⁿ. Приравняем её к θ - вектору, а нейтральным элементом будет функция, тождественно равная нулю на [0,1]. Многочлен степени n на сегменте [0,1] может иметь не более чем корней, а он тождественно равен нулю. Следовательно, нулевыми являются коэффициенты. Итак, равенство нулю линейной комбинации влечёт за собой равенство нулю всех коэффициентов линейной комбинации, значит, система векторов 1,x,x²,...,xⁿ линейно независима.

2. Покажем это иначе. Пусть n - произвольное натуральное число. Положим:

y₁=x,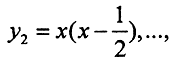

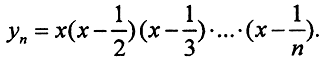
Докажем, что система векторов {y₁,y₂,...,y_n} является линейно независимой. Запишем равенство:

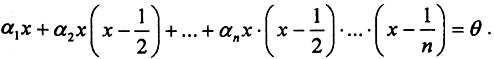
Положив последовательно 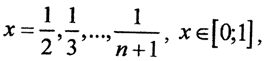получим α₁=α₂=...=α_n=0. Таким образом, равенство α₁y₁+α₂y₂+...+α_ny_n=θ влечет за собой равенство α₁=α₂=...=α_n=0. Следовательно, векторы {y₁,y₂,...,y_n} линейно независимы. Так как n - любое натуральное число, то векторное пространство всех непрерывных функций, заданных на отрезке [0,1], не имеет конечной системы линейно независимых векторов, для которых всякая система, содержащая на один вектор больше, была бы линейно зависима. Поэтому в этом пространстве нельзя ввести понятие конечной размерности.