Введение

Функциональный анализ возник в результате взаимодействия и обобщения идей, концепций и методов математического анализа, геометрии, высшей и линейной алгебры. С одной стороны, он объединяет сейчас чуть ли не все области математики, а с другой стороны, потребности теоретической физики, численных методов, математического программирования делают его необходимым для физиков, прикладников и инженеров, использующих в своей практике современные математические методы.

Многие задачи из различных областей, как математики, так и приложений, часто обладают одинаковыми особенностями и свойствами. Это позволяет строить их абстрактные модели, избегая несущественных деталей. При таком подходе рассматривается множество элементов, природа которых не указана, но они удовлетворяют заданным аксиомам. Теория тогда состоит из логических следствий, то есть теорем, которые следуют из аксиом. Эти теоремы можно применить к каким угодно множествам, удовлетворяющим тем же аксиомам. У любой такой абстрактной модели будут различные конкретные реализации. В алгебре этот подход приводит к появлению полей, колец, групп и так далее.

В функциональном анализе используется понятие абстрактного пространства как множества элементов, удовлетворяющих определенным аксиомам, различные наборы которых дают различные типы абстрактных пространств. В зависимости от природы пространства его носители называют точками, векторами, операторами, событиями и т. д. На этих множествах должна быть задана возможность непрерывного перехода от одних элементов к другим. Поэтому ключевое понятие функционального анализа, одна из его главных конструктивных идей, это идея сходимости последовательности элементов носителя (точек) пространства, которая опирается на идею бесконечности. Идея сходимости позволяет ввести понятие непрерывности отображения, однако в самом общем случае это делается на языке топологических пространств. Все остальные пространства функционального анализа можно рассматривать как частные случаи топологических пространств.

Рассмотрим стандартные пространства функционального анализа. На носителях Х, не наделённых линейной структурой, можно ввести понятие метрики, которое обобщает понятие расстояния между элементами х∈Х в обычном геометрическом пространстве, и построить, таким образом, метрические пространства. Обобщением метрических пространств являются топологические пространства. Любое метрическое пространство - топологическое, обратное, вообще говоря, неверно. На носителях Х, наделённых линейной структурой, можно ввести как метрику, так и норму (длину) векторов, свойства которой являются обобщением свойств длины векторов в обычном геометрическом пространстве, и построить, таким образом, нормированные пространства. Нормированные пространства всегда метрические и, следовательно, топологические. Обратное, вообще говоря, неверно. Это такие пространства, как эвклидовы, гильбертовы и банаховы. Эвклидово пространство - это нормированное пространство, в котором норма вводится через скалярное произведение. Часто бесконечномерные эвклидовы пространства называют предгильбертовыми, потому, что гильбертовы пространства - это полные эвклидовы пространства. Банаховы пространства - это полные нормированные пространства. То есть гильбертовы пространства это банаховы пространства, в которых норма вводится через скалярное произведение. Часто удобно говорить о пространствах со скалярным произведением. Наиболее общими пространствами, фигурирующими в функциональном анализе, являются топологические пространства. Соотношения между бесконечномерными пространствами отображены на рисунке.

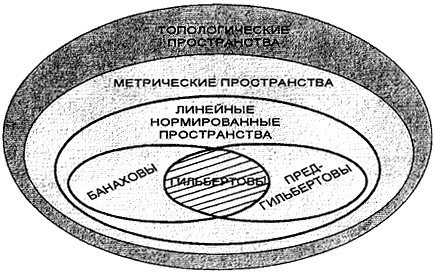
Введение в функционированный анализ

Этот текст следует рассматривать как программу, потому что задачей этой книги и является определение всех этих пространств и их простейших свойств. Коротко напомним то, что понадобится в дальнейшем.

1. Отображения и отношения. Отображение (функция) f из X в Y (обозначается 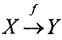) - это правило, которое каждому элементу множества D(f)⊂ X, где D - область определения отображения f, ставит в соответствие единственный элемент множества R(f)⊂ Y, где R(f) - множество значений отображения f. Если X и Y - числа, то f - числовая функция. Если X и Y - не числа, то f - оператор, если X - не числа, а Y - числа, то f - функционал. Отображение сюръективно, если R(f)=Y, инъективно, если x₁≠x₂⇒f(x₁)≠f(x₂), биективно, если оно одновременно инъективно и сюръективно.

На некотором множестве X задано отношение ρ, если ∀x,y ∈ D(X)⊂X*X можно сказать, находятся ли они в отношении ρ или нет. Здесь X*X - декартово произведение, как и в курсе дискретной математики. Отношение рефлексивно, если ∀x∈ D(X) имеет место xρx. Отношение симметрично, если ∀x,y ∈ D(X)⊂X xρy→ yρx. Отношение транзитивно, если ∀x,y ∈ D(X)⊂X из xρy и yρz следует, что xρz. Отношение, обладающее свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности. Это обозначается так: ∀x,y ∈ D(X)⊂X x∼y. Отношение эквивалентности разбивает множество на непересекающиеся подмножества - классы эквивалентности. В самом деле, пусть A≠ B - два множества и D = A∩B≠∅. То есть ∃ d∈D: (d∈A)∧(d∈B). Тогда ∀a ∈A d∼a и ∀b∈B d ∼b. Отсюда в силу транзитивности a∼b, но тогда A=B. Множество классов эквивалентности данного множества называется фактор-множеством, а операция построения фактор-множества называется факторизацией.

2. Бесконечные множества. Множества A и B называются эквивалентными или равномощными, если существует хоть одна биекция f: 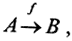то есть отношение равномощности есть отношение эквивалентности. Множество, допускающее биекцию с любым куском натурального ряда чисел N, называется конечным. Число элементов n в конечном множестве А называют его мощностью: cardA=n. Множество, допускающее биекцию со всем натуральным рядом чисел N, называется счетным. Мощность счетного множества называется алеф ноль. Легко показать следующие утверждения:

1. Любое подмножество счётного множества A конечно или счётно.
2. Из любого бесконечного множества A можно выделить счётное подмножество B⊂A так, что множество A/B останется бесконечным.
3. Объединение 1) конечного числа конечных множеств конечно, 2) счётного числа конечных множеств счётно, 3) конечного числа счётных множеств счётно, 4) счётного числа счётных множеств счётно. (Доказательство заключается в указании процедуры пересчёта.)

Точно так же, указав способ пересчёта, можно показать счётность множества рациональных чисел, расположив их в виде бесконечной матрицы, выбрасывая совпадающие элементы. Однако множество точек отрезка [0,1] не счётно (теорема Кантора). Мощность несчётного множества A точек отрезка [0,1] cardA=A₁называется мощностью континуума или алеф один. Существуют множества с мощностью, большей, чем A₁. Согласно теореме Кантора о больших алефах,каково бы ни было множество A, множество его подмножеств P(A) имеет большую мощность.Дедекинд определил бесконечное множество, как такое, которое эквивалентно хоть одному собственному подмножеству.

3. Алгебраические структуры. В простейшее варианте рассмотрим два множества М и S произвольной природы, a x,y,z - три элемента этих множеств. Правило (закон), по которому упорядоченной паре элементов х и у ставится в соответствие элемент z (один и только один), называется бинарной операцией или законом композиции, результат этой операции (элемент z) называется композицией, а элементы х и у называются операндами. Если x,y,z∈M (одному из множеств), то закон композиции называется внутренним, а множество М называется замкнутым относительно этого закона (этой бинарной операции), а если операнды принадлежат разным множествам, а композиция одному из них (например, x,y∈M, z∈S), то такая бинарная операция называется внешним законом. Алгебраической структурой называется множество (носитель структуры) М с заданными на нём одним или двумя внутренними законами композиции, которые обозначаются * и ○ и часто называются "сложение" и "умножение". Эти законы композиции могут обладать или нет определенными свойствами, которые, в свою очередь, задают ту или иную структуру множества М, которое называется носителем алгебраической структуры. Имея дело с алгебраической структурой (АС), следует соблюдать три правила и знать свойства законов.

1. Природа и характер носителя алгебраической структуры не обсуждается.
2. Природа и характер операций, порождающих данную алгебраическую структуру на множестве М, не обсуждается.
3. Все рассуждения проводятся только на абстрактном уровне.

Свойства внутренних законов композиции:

x*y=y*x - коммутативность;

x*(y*z)=(x*y)*z - ассоциативность;

x○(y*z)=(x○y)*(x○z) - дистрибутивность слева операции ○ относительно операции *;

(x*y)○z=(x○z)*(y○z) - дистрибутивность справа операции ○ относительно операции *.

Аналогично определяется дистрибутивность относительно операции . Законы композиции наделяют элементы множества М некоторыми свойствами, верными или нет только при этих законах. Другими словами, на множестве М при действии данного закона с его свойствами появляются выделенные элементы, т.е. оно становится структурированным (откуда и понятие АС). Элемент e∈M называется нейтральным относительно данного закона *, если e*x=x*e=x ∀x∈M. Если нейтральный элемент есть, то он единственен. Пусть множество М содержит нейтральный элемент e∈M относительно операции *. 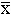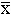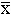Элемент ∈M называется симметричным (обратным, противоположным) элементу x∈M, если *x=x*=e.

Определяя на множестве произвольной природы M один или два закона композиции, наделяя эти законы какими-то из перечисленных свойств и задавая структуру M относительно этих свойств, мы получим различные алгебраические структуры, перечисленные в таблице, задающей аксиомы алгебраических структур.

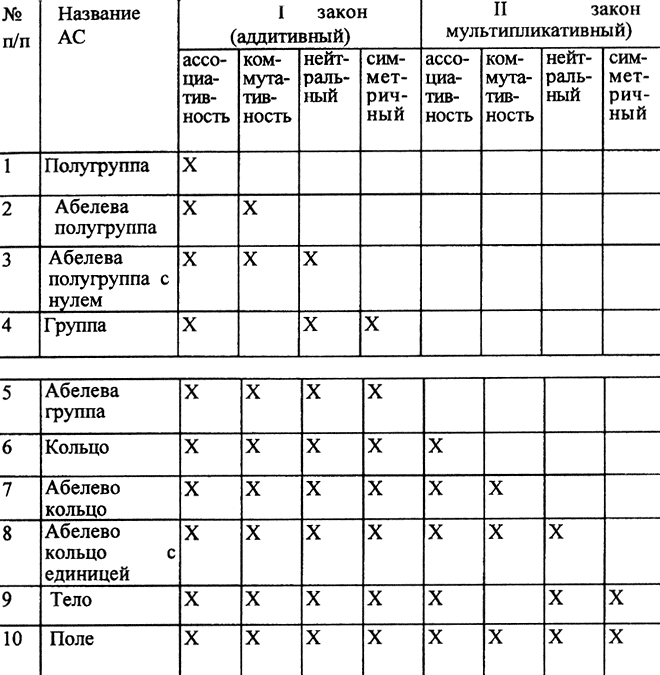
Значок Х означает, что данный закон обладает этими свойствами, а множество М имеет относительно этого закона соответствующие элементы. При этом полагается, что:

1) мультипликативный закон, если он определен, дистрибутивен слева и справа относительно аддитивного.

2) симметричный элемент мультипликативного закона определен для всех элементов носителя АС (множества М), кроме нейтрального относительно аддитивного закона.

Замечание.В дальнейшем тексте начало и конец любого рассуждения будем отмечать значком , а если рассуждение проводится "от противного", то это отмечается значком 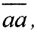от латинского ad absurdum приведение к нелепице.