72. Восстановление записи

В памятной книжке найдена запись, воспроизведенная на рис. 62. Эта запись оказалась залитою в некоторых местах чернилами так, что нельзя разобрать ни числа проданных кусков, ни первых трех цифр полученной суммы. Спрашивается, можно ли по сохранившимся данным узнать число проданных кусков и всю вырученную сумму?

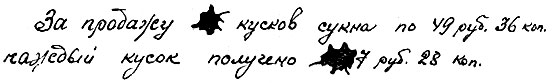
Рис. 62

Решение. По условию вся вырученная сумма, очевидно, не превышает 9997 руб. 28 коп. Значит, число проданных кусков не более 999728 : 4936, т. е, не более 202 кусков.

Последняя цифра неизвестного числа кусков должна быть такова, чтобы она, будучи умножена на 6, давала произведение, оканчивающееся на 8; такая цифра может быть 3 или 8.

Положим, что последняя цифра неизвестного числа кусков равна 3. Стоимость трех кусков равна 14808 коп. Вычитая это число из вырученной суммы, мы должны получить число, оканчивающееся на 920.

Если предположить, что последняя цифра равна 3, то вторая от конца цифра может быть или 2, или 7, так как только эти цифры, будучи умножены на 6, дают произведения, оканчивающиеся на 2.

Положим, что неизвестное число оканчивается на 23. Вычитая стоимость 23 кусков из всей вырученной суммы, получим число, оканчивающееся на 200. Третья цифра может быть или 2, или 7; но так как неизвестное число не превосходит 202, то наше предположение неверно.

Если бы мы предположили, что неизвестное число оканчивается на 73, то третья цифра была бы равна 4 или 9; такое предположение тоже неверно.

Итак, последняя цифра не может быть 3; остается предположить, что она равна 8. Рассуждения, подобные предыдущим, покажут нам, что вторая цифра может быть или 4, или 9; из этих двух предположений верным может быть только второе.

Задача имеет одно решение: число проданных кусков равно 98, вся вырученная сумма равна 4837 руб. 28 коп.