Математическое моделирование биологических сообществ (Ю. М. Свирежев, доктор физико-математических наук)

Математическое моделирование биологических сообществ

За последние годы поток работ, посвященных математическому моделированию в биологии, резко возрос. Сложилась ситуация, при которой любой человек, мало-мальски овладевший тем или иным математическим аппаратом, обязательно строит "модель", и обязательно "математическую" или "кибернетическую". Казалось бы, что это явление можно только приветствовать. Однако Дело обстоит не так просто, как этого хотелось бы.

В биологии, кроме большого объема чисто описательного материала, существует много различных моделей, достаточно строгих и логически безупречных, но изложенных на языке, отличном от математического, причем прямой перевод зачастую невозможен. Необычайно повезло, может быть, генетике, где менделевские законы записываются на математическом языке (вплоть до того, что для их описания могут быть использованы формальные алгебраические структуры).

Теория микроэволюции - это также чисто математическая теория, которая легко и изящно может быть изложена в рамках некоторой аксиоматической формальной теории. По-видимому, в силу этих причин наибольшее развитие получили математическая генетика и теория микроэволюционных процессов, где чисто математическими средствами получен ряд очень хороших результатов. В остальных областях биологии успехи математического моделирования гораздо скромнее. (Мы специально не рассматриваем модели чисто физических и химических процессов, происходящих в биологических системах, поскольку здесь используются хорошо известные закономерности и уже достаточно разработанный язык.) Правда, в этих областях мы можем идти по пути создания феноменологических моделей, моделей, позволяющих использованием нового языка для описания уже известных фактов более удачно и удобно представить имеющуюся информацию. И делать более разумные выводы, которых в противном случае мы просто не смогли бы сделать из-за обилия информации. Другими словами, за деревьями не увидеть леса...

По-видимому, одна из основных задач моделирования в биологии - это представление больших объемов информации в виде небольшого числа блоков, описывающих некоторые глобальные характеристики биосистем, с которыми удобно было бы работать. Перефразируя известное высказывание Р. Беллмана, можно сказать, что эта задача - борьба с "проклятием размерности", борьба с многомерностью существующей информации, умение так ее агрегировать, чтобы, с одной стороны, не потерять ничего существенного, а с другой - не утонуть в ней. Ясно, что принцип выделения таких блоков должен учитывать реально существующее в природе деление биосферы на некоторые элементарные единицы (функциональные или пространственные).

Вторая важная задача - как из этих элементарных блоков строить модели более сложных систем, так, чтобы они не "разваливались", т. е. чтобы результаты моделирования были похожи на реальную действительность. Здесь можно сформулировать следующее, пользуясь термином В. И. Вернадского, "эмпирическое обобщение": любое достаточно долго существующее биологическое сообщество представляет собой устойчивую гомеостатическую систему. Механизмы, обеспечивающие устойчивость сообщества, могут быть самыми разнообразными. По-видимому, требование устойчивости модели может служить тем основным принципом, которому должна удовлетворять модель реально существующей биологической системы.

Понятие устойчивости сообщества

В экологии уже давно предпринимались попытки экспериментального определения такой, кажется, понятной характеристики сообщества, как его стабильность или устойчивость.

Интуитивно ясно, что биогеоценоз, экосистема, биологическое сообщество, существующие в более или менее неизменном виде достаточно длительное время, обладают некоторой внутренней способностью противостоять возмущающим факторам, которые в изобилии поставляет внешняя среда (в том числе и человек). Именно эту способность биологических систем обычно называют "устойчивостью", или "стабильностью". Естественно, что прежде чем использовать это свойство при построении или отборе моделей, необходимо дать ему операционное определение, которое позволило бы измерять это свойство и сравнивать по нему различные системы.

С другой стороны, существует развитая математическая теория устойчивости, в которой определение устойчивости дается совершенно строго. Если мы имеем достаточно "хорошую" (в смысле адекватности и полноты описания) математическую модель биологического сообщества (в терминах дифференциальных или разностных уравнений), тона вопрос об устойчивости реального сообщества (точнее, об устойчивости его некоторого стационарного состояния) можно ответить, исследуя нашу модель обычными методами теории устойчивости. Система будет устойчива, если ее траектория в фазовом пространстве не будет выходить за пределы заданной ограниченной области при некоторых конечных возмущениях достаточно широкого спектра. Подобное определение отвечает интуитивным представлениям экологов, и часть из них вполне устраивает. Но в практике этот путь исследования зачастую невозможен, поскольку создание хорошей модели - задача непростая. Поэтому весьма заманчивой представляется идея найти такую достаточно простую и легко определяемую из эксперимента величину, что по ее значению для конкретного сообщества можно было бы судить о степени его устойчивости или стабильности.

Очевидно, что общие термодинамические концепции (например, связанный со вторым законом термодинамики принцип стабильности) должны быть приложимы и к экологическим системам. Согласно этим концепциям любая замкнутая система с протекающим через нее потоком энергии (будь то биосфера или пруд) с большей вероятностью развивается в сторону некоторого устойчивого состояния и в ней с необходимостью должны вырабатываться саморегулирующие механизмы. Когда это состояние достигнуто, то перенос энергии обычно идет в одном направлении и с постоянной скоростью, что соответствует термодинамическому принципу стабильности. Классическим примером такой проточной системы является система "хищник - жертва". К сожалению (и в этом свойство всех слишком общих концепций), термодинамический принцип стабильности не дает нам метода, который позволил бы эффективно судить о степени стабильности конкретных биологических сообществ или экосистем.

В последнее десятилетие ведется оживленная дискуссия по вопросу об определении понятия "экологическая устойчивость (стабильность)" и о том, как ее измерять. Суммируя самые разнообразные высказывания экологов по этому вопросу, можно выделить некоторую систему требований к биологическим сообществам различных уровней организации. Все эти требования обычно называются одним словом - устойчивость.

Первое - это требование известной неизменяемости во времени целого географического региона. Вторая группа требований - сохранение числа видов в данном сообществе в течение достаточно длительного времени. Пожалуй, именно это экологическое определение ближе всего к математическому определению устойчивости. И наконец, третья группа требований относится скорее к популяциям. Считается, что сообщество устойчиво, или стабильно, если численности составляющих его популяций не испытывают резких колебаний. Это определение более близко к физическому, чем к математическому. (В статистической физике система считается стабильной, если малы вероятности больших флюктуации, могущих увести ее далеко от равновесного состояния и даже разрушить.)

Подобный разнобой в определении основного понятия говорит о том, что не существует еще ясного понимания в вопросе об устойчивости биологических сообществ В ходе дискуссий по этому вопросу возникают попытки как-то усовершенствовать понятие устойчивости. Расскажем об одной такой попытке. В последнее время в работах профессора К. С. Холдинга (Канада) развивается идея, что одной лишь устойчивости, понимаемой в смысле ее математического определения, недостаточно для характеристики поведения системы. Например, система может быть устойчивой в нескольких областях фазового пространства, но характер устойчивых состояний может быть принципиально различным. В частности, из-за случайных факторов или благодаря вмешательству человека может произойти вымирание одного или нескольких видов и, следовательно, исчезновение соответствующих трофических связей. Поэтому наряду с устойчивостью предлагается рассматривать еще и такое свойство, как "упругость" - способность системы сохранять свои внутренние взаимосвязи при возмущении ее состояния. Для нескольких областей устойчивости это означает, что система допускает лишь такие переходы из одной области в другую, которые не приводят к исчезновению популяций из сообщества.

Устойчивость и разнообразие

Очень распространены попытки связать устойчивость сообщества с какой-либо другой его характеристикой, которую можно было бы измерить. Например, среди экологов считается почти аксиомой, что более сложные по своей структуре, более богатые по числу входящих в них видов сообщества и более устойчивы. По-видимому, это объясняется следующим рассуждением. Различные виды По-разному приспособлены к изменениям окружающей среды. Поэтому широкий набор видов может лучше реагировать на разнообразные изменения внешней среды, чем сообщество, состоящее из малого числа видов, а следовательно, первое устойчивее, стабильнее второго.

Вероятно, этим и обусловлены попытки использовать в качестве меры устойчивости информационную энтропию (или некоторый ее аналог). Например, "разнообразие" сообщества определяется как

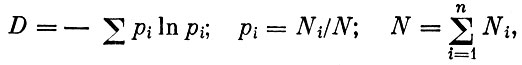
где n - число видов в сообществе, N_i - численность i-того вида, а "стабильность"

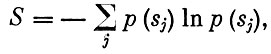
где р (s_j) - вероятность переноса энергии по определенному пути s_j. Считается, что элиминация какого-либо вида из сообщества и разрушение соответствующих трофических связей оказывает меньшее влияние на сообщество с большим S. Аналогично и для величины D: чем более "разнообразно" сообщество, тем более оно устойчиво. При этом эволюция должна приводить сообщество к некоторому устойчивому состоянию, или равновесию.

Исходя из этих концепций, можно сказать, что максимально устойчивое сообщество должно обладать в этом состоянии максимумом разнообразия.

Но максимально возможному значению разнообразия соответствует структура сообщества, где все виды встречаются с одинаковой частотой. Отсюда следует, что наиболее устойчивым является сообщество, в котором не существует количественной иерархии видов. Однако это противоречит результатам наблюдений над природными сообществами. (Аналогичные соображения можно высказать и по поводу S и по поводу других энтропийных мер, а их было предложено немало.) По-видимому, использование этих величин в качестве мер устойчивости все же не совсем оправданно. Но ради объективности нельзя умолчать о том, что во многих лабораторных (и не только лабораторных) сообществах на ранних стадиях развития при движении к устойчивому состоянию действительно наблюдается увеличение разнообразия. Из этого можно сделать вывод, что разнообразие на таких стадиях характеризует устойчивость сообщества (в том смысле, что вдоль траектории, ведущей к устойчивому нетривиальному стационарному состоянию, разнообразие возрастает; но не на всей траектории, а только лишь на начальном ее участке).

В чем же причина возникновения этих парадоксов? Скорее всего в формальном применении аппарата теории информации к системам, к которым он непримевим. Как больцмановская энтропия в статистической физике, так и информационная энтропия в теории информации имеют смысл лишь для ансамблей из слабо взаимодействующих частиц или каких-либо других объектов. Введение энтропийной меры для таких множеств вполне обоснованно. Но как только мы имеем дело с системами, элементы которых сильно взаимодействуют между собой, энтропийная мера неудовлетворительна. А биологические сообщества, где конкурентные взаимоотношения наиболее сильно проявляются вблизи положения равновесия и вся структура которых в основном определяется не характеристиками, присущими собственно виду, а характеристиками межвидовых взаимоотношений, представляют собой именно системы с сильными взаимодействиями.

С этой точки зрения понятна применимость энтропийной меры на ранних стадиях эволюции общества. Все дело в том, что на этих стадиях, вдали от положения равновесия, конкуренция еще слаба, конкурентные давления еще малы и сообщество вполне может рассматриваться как система со слабыми взаимодействиями.

Трофическая структура сообщества. Понятие сложности

Природа обнаруживает перед исследователями громадное разнообразие биологических видов. Отдельные группы видов, находясь в определенных взаимоотношениях между собой, образуют биологические сообщества той или иной структуры. Исследование структуры сообщества сводится к выяснению типов связей между составляющими его видами (межвидовых отношений). Что касается классификации типов межвидовых отношений, то здесь в экологии весьма плодотворно работает идея классифицировать их не по механизмам взаимодействия между особями видов - иначе классификация получалась бы необозримой,- а по тому количественному влиянию на Уровне целых популяций, которое оказывает прирост численности того или иного вида. Так возникает 5 типов взаимодействий между видами: "хищник - жертва" (или "паразит - хозяин"), конкуренция, симбиоз, аменсализм и комменсализм,- конкретная комбинация которых и определяет структуру сообщества. Например, травоядные поедают зеленую массу луговых цветов ("хищничество"), будущий урожай которых во многом зависит от насекомых-опылителей, питающихся пыльцой растений (симбиоз); насекомые поедаются птицами; близкие виды птиц питаются примерно одними и теми же видами насекомых (конкуренция) и т. д.

Первое и естественное приближение к анализу структуры сообщества, ставшее уже, можно сказать, общепринятым среди экологов, состоит в построении графа, вершины (узлы) которого соответствуют входящим в сообщество видам, а ребра - взаимодействиям типа "хищник - жертва" между видами (другими словами - кто кого ест). Этот граф носит название трофической сети, или пирамиды. В нем естественно выделяются различные трофические уровни - их может быть несколько; виды, принадлежащие одному уровню, находятся либо в состоянии конкуренции за одни и те же жизненные ресурсы, либо образуют коалицию. Виды одного уровня служат пищей видам более высокого уровня. На рис. 7 приведен пример такой трофической пирамиды из 6 видов, в которой выделяются три трофических уровня.

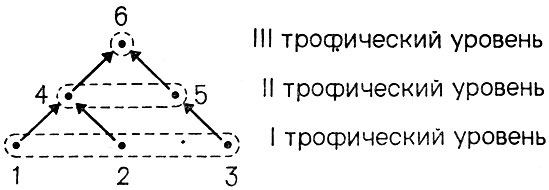
Рис. 7. Пример трофической пирамиды

Ясно, что подобные конструкции не в состоянии отобразить структуру сообщества с различными типами связей из вышеприведенной классификации - для этого требуются более сложные конструкции, которые носят название знаковых ориентированных графов. Однако несомненное преимущество трофических пирамид - в их простоте и наглядности.

Видно, что в таком сообществе естественно выделяются вертикальная и горизонтальная структуры. Вертикальная структура отражает взаимоотношения хищничества или, в общем случае, такие трофические связи, при которых рост биомассы одного вида подавляет рост биомассы второго и, в свою очередь, рост биомассы второго вида стимулирует рост биомассы первого. Горизонтальная структура задает взаимоотношение видов на одном уровне (коалиция или конкуренция). Трофическая пирамида не дает этого описания, хотя очевидно, что эти взаимодействия очень важны для стабилизации численности видов на одном уровне.

Анализу взаимоотношений видов на одном трофическом уровне весьма помогает понятие экологической ниши. Допустим, что каждый из видов, конкурирующих за некоторый ресурс, характеризуется определенной точкой в пространстве параметров данного ресурса и некоторой "функцией потребления", которая является, по сути дела, плотностью распределения на множестве значений параметров со средним в этой точке. Например, каждый вид имеет предпочтительный размер потребляемой пищи, а вероятность потребления пищи иного размера распределена нормально с предпочтительным размером в качестве среднего. Тогда точка в пространстве ресурсов и соответствующая ей "функция потребления" определяют экологическую нишу данного вида. Под пересечением ниш понимается пересечение "зон потребления" для видов в пространстве ресурсов. Естественно считать, что конкуренция тем сильнее, чем больше перекрытие экологических ниш конкурирующих видов.

По поводу иерархии уровней, которая существует в трофической пирамиде, следует отметить, что введение нового уровня в сообщество, или элиминация его, может существенно изменить поведение системы. Например, двухуровневая система, устойчивая в целом, может обладать неустойчивостью внутри одного уровня (при постоянном значении численностей другого уровня), и наоборот, система, устойчивая внутри каждого уровня, может оказаться неустойчивой в целом.

Интуитивно понятно, что чем более богатую и разветвленную трофическую сеть имеет биологическое сообщество, тем более сложно оно устроено. На этом интуитивном представлении основано и определение меры сложности:

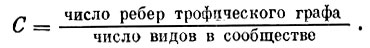
Для примера рис. 1 С = ⁵/₆. Для классической модели "хищник - жертва" 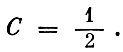Если предположить, что все n видов сообщества соединены между собой трофическими связями (максимально сложное сообщество), то 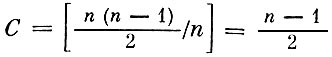- максимально возможное значение меры сложности. Очевидно, что для системы с несколькими уровнями значение С должно быть меньше (например, для гипотетической системы из n видов, на каждом трофическом уровне которой по одному виду ).

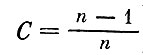Пока логика этих рассуждении не вызывает возражений (хотя и можно говорить, что здесь не учитывается количество энергии или биомассы, передаваемой по каждому трофическому пути). Но затем обычно делается логический скачок, и уже говорится, что чем сложнее сообщество, тем оно устойчивее, или стабильнее, т. е. снова одно понятие подменяется другим.

Устойчивость для моделей биологических сообществ

Мы предлагаем следующий выход из этого замкнутого круга противоречий. Вместо того чтобы рассматривать различные определения для одного и того же объекта, мы заменим сам объект и будем пользоваться существующими определениями устойчивости, но не для биологических сообществ, а для их математических моделей, записанных в виде дифференциальных, или разностных уравнений. Конечно, здесь мы также совершаем подмену, и остается открытым вопрос о мере адекватности модели моделируемому объекту. Остается утешаться тем, что этот вопрос разработан гораздо полнее как с математической, так и с гносеологической точки зрения.

Поэтому в дальнейшем всюду, говоря о биологических сообществах и биосистемах, мы будем иметь в виду их математические модели, в частности, модели, предложенные итальянским математиком В. Вольтерра в 20-х годах нашего века и их последующие модификации. Можно показать, что модели этого типа могут быть получены из общих законов сохранения и некоторых весьма правдоподобных гипотез о характере взаимодействия между составляющими сообщество видами.

Исследование устойчивости в рамках математических моделей динамики численностей биологических популяций, наряду с общими чертами, определяемыми спецификой моделируемого объекта, имеет и свои особенности в зависимости от математического аппарата, использованного при построении модели. Так, из "биологических" соображений следует, что в любой математической модели имеют смысл лишь те траектории системы, для которых значения численностей видов неотрицательны. С другой стороны, если мы имеем дело с моделями в виде систем обыкновенных дифференциальных уравнений, то под устойчивостью может пониматься устойчивость по Ляпунову некоторого стационарного решения; если модель построена в форме уравнений в частных производных, то устойчивость стационарного распределения в среднеквадратичном смысле, для стохастических дифференциальных уравнений - устойчивость по вероятностной мере и т. д.

Следует заметить, что результаты анализа устойчивости в моделях сообществ не всегда согласуются с привычными для экологов гипотезами. Такая ситуация наблюдается, например, в вопросе, влечет ли увеличение сложности экосистемы повышение ее стабильности. В ряде исследований показано, что вероятность устойчивости сложной экосистемы возрастает лишь в определенных пределах увеличения показателя сложности С, а в некоторых случаях с ростом С эта вероятность убывает. Эти противоречащие интуитивным представлениям экологов математические результаты привели к возникновению целого направления в исследованиях по математической экологии, которое получило название проблемы "сложность против устойчивости".

О соотношении между скоростями изменения общей биомассы сообщества его "квазиразнообразия"

Пусть мы имеем вольтерровскую модель биологического сообщества из n взаимодействующих видов, численности которых N_i(t). Если в этой модели существует нетривиальное положение равновесия с численностями N^*_i>0, то естественно поставить вопрос, при каких условиях это равновесие будет устойчиво (в математическом смысле) и эволюция сообщества не будет сопровождаться элиминацией видов? Оказывается, что если вдоль траектории эволюции сообщества выполняется неравенство 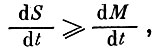то сообщество эволюционирует к этому нетривиальному равновесию, а виды не элиминируются. Здесь 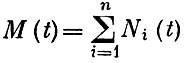общая биомасса сообщества, a 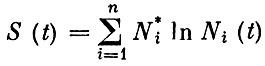некоторая энтропийная мера разнообразия, несколько отличающаяся от "разнообразия", введенного ранее. Мы назвали ее "квазиразнообразием" сообщества. Поскольку вдоль траектории, ведущей к устойчивому нетривиальному положению равновесия сообщества, 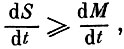то это означает, что при любой допустимой эволюции сообщества, в процессе которой не происходит элиминации видов, скорость возрастания суммарной биомассы не должна превышать скорости увеличения "квазиразнообразия" сообщества, а при уменьшении биомассы для сохранения устойчивости сообщества его "квазиразнообразие" должно падать медленнее, чем суммарная биомасса.

Доказанным утверждением вполне можно пользоваться для определения устойчивости сообщества. Если при достаточно длительных наблюдениях за флюктуациями численностей видов это неравенство выполняется, то можно говорить об устойчивом (или стабильном) сообществе. К сожалению, для этого необходимо заранее знать его нетривиальное стационарное состояние.

Поскольку в равновесии величина (S - М) достигает максимума, то, по аналогии с механикой, величину 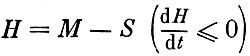можно назвать "энергией сообщества". Тогда при эволюции сообщества к нетривиальному равновесию его "энергия" либо монотонно убывает, стремясь к своему минимально возможному значению, либо вообще не изменяется; в последнем случае система может иметь замкнутые траектории. По-видимому, состояние сообщества можно характеризовать его "энергией", причем чем ниже значение "энергии", тем более устойчиво сообщество. По сути дела, Н является энергетической мерой устойчивости.

Об иерархической устойчивости биологических сообществ и временной стабилизации

Когда мы говорим, что у нас есть "достаточно хорошая" математическая модель биологического сообщества, это означает, в частности, что она обладает одним или несколькими стационарными состояниями и некоторые из них должны быть устойчивы. Требование это отражает тот факт, что реальные биологические системы находятся в состоянии некоторого динамического равновесия. Ниже на простом примере будет показано, что требование глобальной устойчивости всей системы не обязательно, а может быть заменено требованием "иерархической устойчивости", под которым понимается следующее. Система организована таким образом, что отдельные ее блоки устойчивы, но вся система может и не обладать устойчивостью. Однако эта неустойчивость либо проявляется на больших отрезках времени (превосходящих время существования системы), либо неустойчивость некоторой подсистемы стабилизируется блоком, расположенным иерархически выше.

Рассмотрим конкретную систему, которая состоит из растений и микроорганизмов, разлагающих опад и производящих питательный субстрат для растений. В пользу такого упрощения системы свидетельствует тот факт, что свыше 90% биомассы и энергии биогеоценозов заключено ИУШННО в этих компонентах, а остальные можно рассматривать как возмущения для этой системы.

Блок-схема довольно общего вида модели такой системы приведена на рис. 8. Заметим, что именно такая структура потоков вещества и энергии характерна для биогеоценозов и экосистем суши.

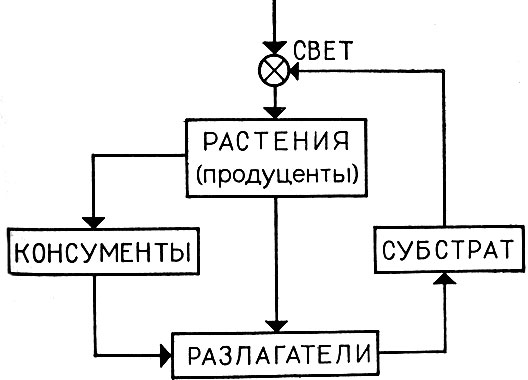
Рис. 8. Блок-схема потоков массы и энергии в экосистеме

Изучение этой модели показало неустойчивость ее стационарных состояний. По-видимому, дело в том, что в модели не принималась в расчет существенная разнома-сштабность времен каждой компоненты. Характерное время для компоненты "растения" фактически много больше характерного времени для микроорганизмов (и соответственно для субстрата). Если учесть это обстоятельство (введением малого параметра, изменяющего должным образом временной масштаб для отдельных компонент), то получается следующая картина. Биомасса растений медленно эволюционирует, подчиняясь в основном, вследствие Достаточно большого характерного времени, периодическим воздействиям изменяющихся внешних параметров (свет, температура, влажность и т. п.). Вокруг этой меняющейся траектории с гораздо большей скоростью, но никуда не уходя от нее, изменяется траектория подсистемы "микроорганизмы - субстрат". Вводя временную иерархию, мы получили иерархию структурную, где поведение высшего члена определяет общее поведение низших, а само определяется причинами, внешними для всей системы. Этот частный пример показывает, насколько важно учитывать иерархичность временной структуры.

Еще один пример дает рассмотрение модели реальной биосистемы - популяции божьих коровок Adalia bipunctata, содержащей генетически детерминированные красную и черную формы. Эти формы отличаются тем, что одна из них интенсивнее размножается летом, а другая лучше переносит условия зимы. Таким образом, имеется периодически меняющееся давление естественного отбора на эти формы. Если бы постоянно поддерживались зимние или летние условия, то популяция содержала бы только одну форму - красную или черную. Но периодически меняющееся давление отбора поддерживает систему в промежуточном состоянии. Можно показать, что при определенных условиях это состояние устойчиво. Этот пример демонстрирует, как периодическое изменение условий внешней среды может стабилизировать систему, которая при постоянстве внешней среды была бы неустойчивой.

Рассмотренные примеры указывают на важную роль временной стабилизации в биологических системах, которые обычно характеризуются наличием большого числа возможных стационарных состояний. Некоторые из них соответствуют вырождению или гибели системы. Периодические же колебания внешней среды удерживают систему от перехода в эти состояния. Подобный механизм мы и называем временной стабилизацией. По-видимому, он широко распространен в живой природе.

Методы системного анализа при моделировании биологических сообществ и биосферных процессов

Использование методов системного анализа при моделировании биологических сообществ, экосистем, биогеоценозов и всей биосферы в целом - это необходимость, порожденная принципиальной сложностью проблемы. Если не останавливаться на сложности самих объектов исследования, какие трудности можно выделить при организации таких исследований?

Необходимость объединения специалистов разных типов и разных специальностей. До сих пор при изучении биогеоценозов, экосистем, популяций и т. п. организация исследований ставится таким образом, что (может быть, даже с излишней детализацией) изучаются отдельные и не всегда самые существенные компоненты биосферных систем. Энтомологи изучают насекомых, зоологи - животных, почвоведы - различные типы почв,- объект изучения определяется профессиональной ориентацией и зачастую личными интересами того или иного исследователя. Все это приводит к тому, что некоторые компоненты системы исследуются слишком подробно, а другие не исследуются совсем.

Необходимость объединения информации, различающейся как по способам получения, так и, что особенно существенно, по способам представления. Это естественно, поскольку в каждой узкой специальности уже сложились свои, ставшие традиционными методы получения и представления информации.

Необходимость учета разнообразных критериев. Требования различных "заказчиков" к одной и той же биосферной системе могут быть даже противоположными, а их "управления" могут привести к совершенно различным последствиям. Естественно, что только на модели можно проверить различные варианты управлений и выбрать некоторое компромиссное решение.

Единственным способом выпутаться из этих противоречий и существенно облегчить труд естествоиспытателей и экономистов является создание имитационных систем, работающих в режиме диалога "человек - машина". Причем работа в области моделирования должна сразу планироваться как разработка проекта. Какие выгоды можно ожидать от такой организации исследований?

• возможность объединения различных специалистов на базе одной системы;
• возможность совмещения информации;
• становятся видными пробелы, и ясно, какого гипа исследования необходимо заказать;
• появляется возможность не только координации, но и управления исследованиями;
• появление четкой целенаправленности резко увеличивает эффективность научно-исследовательских разработок и уменьшает затраты.

По-видимому, сама система может быть организована по следующему принципу (рис. 9). Нам представляется, что работа над блоком процедур - это выработка того, что называется "гомеостатическим равновесием".

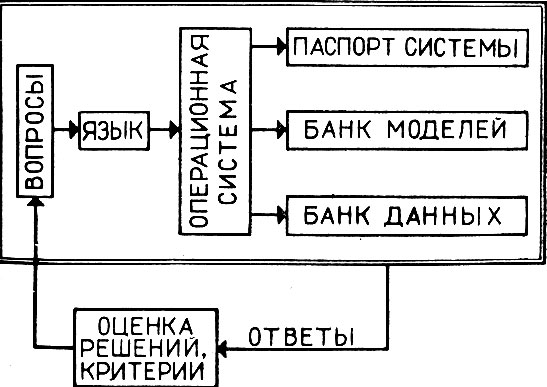
Рис. 9. Блок-схема имитационной системы

На начальной стадии работы модели превалируют над данными. При построении первичной системы моделей используются:

• законы сохранения (это тот костяк, который задает в дальнейшем неизменяемую часть общей структуры, но который не может полностью задать все поведение системы);
• самые общие представления о структуре потоков вещества, энергии и информации в системе (это может быть граф трофических связей, некоторые характеристики Поведенческих реакций и т. п.);
• некоторые представления о воздействии факторов среды на такие общие характеристики, как плодовитость, скорость роста и т. п.

Первичная система моделей содержит определенное число параметров и функций, которые должны быть определены из имеющейся экспериментальной информации - модель должна быть идентифицирована. При этом становится ясным, какой информации не хватает, а какая избыточная. Затем наступает этап верификации модели: проверки правильности модели на той информации, которая не использовалась при построении и идентификации модели. Здесь возникает важная проблема об оптимальном разбиении всей имеющейся информации на три независимых подмножества: 1) подмножество информации, необходимой для построения первичной модели; 2) подмножество информации, необходимой для идентификации; 3) подмножество информации, необходимой для верификации. Естественно, что возникает задача соответствующего планирования экспериментальных исследований, которые позволили бы сформировать эти подмножества. После этого наступает этап уточнения первичной модели и т. д.

Такая последовательная процедура позволяет из большого числа возможных моделей отобрать набор необходимых.

Принципы построения банка моделей

По-видимому, внутренняя организация банка моделей должна соответствовать той естественной классификации, которая имеется в самой биосфере. Согласно В. Н. Сукачеву и Н. В. Тимофееву-Ресовскому, элементарная биохорологическая единица биосферы, производящая в то же время элементарную "биогеохимическую работу", есть не что иное, как биогеоценоз (БГЦ). Существенно, что БГЦ - это реально существующая система, которую можно выделить и для которой характерно преобладание числа внутренних связей над внешними. Это дает основание считать БГЦ до известной степени изолированной системой. Отсюда следует один из подходов к организации банка моделей. В этом банке мы должны иметь достаточно представительный набор моделей "типовых" БГЦ, из которых, связывая их через модели геохимических циклов, можно строить модели систем следующего уровня (ландшафты, регионы и т. п.). Кроме того, в банке должны быть различные модели человеческой активности. Тогда система моделей может выглядеть следующим образом (рис. 10). Предполагается, что модели верифицированы. Задача операционной системы в этом случае заключается в сборке модельной системы из блоков, ее идентификации с использованием банка данных (подготовка к диалогу) и в проведении дальнейшего диалога.

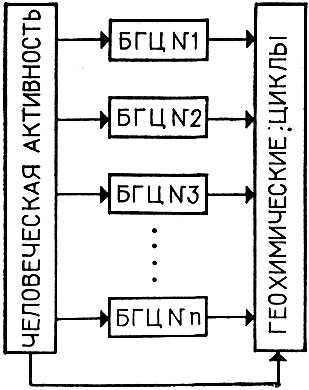
Рис. 10. Структура банка моделей (БГЦ - биогеоценоз)

Концепция БГЦ рассматривает биосферу как пространственно стратифицированную систему без функциональной иерархии подсистем. При этом часто высказывается мнение, что каждый БГЦ сугубо индивидуален, и невозможно выделить сравнительно небольшой набор типовых БГЦ. Но тогда становится бессмысленной сама идея о моделировании. По-видимому, все же это не так. При рассмотрении структуры потоков вещества и энергии в различных БГЦ обращает на себя внимание их "похожесть", которая повторяется и на глобальном уровне. В любом БГЦ можно выделить следующие круговороты: круговорот углерода, по которому БГЦ практически замкнут, круговороты азота и фосфора, круговорот воды. Все вышеперечисленные круговороты могут быть объединены одним энергетическим круговоротом. То, что динамическая структура всех БГЦ практически почти одинакова, позволяет надеяться на однотипность моделей, которые будут отличаться друг от друга в основном за счет различных значений входящих в эти модели параметров.

Методы "системной динамики" и критерии устойчивости

В последнее время большое распространение в моделировании сложных динамических систем получили методы так называемой "системной динамики" Форрестера. Эти методы существенно машинные, основанные на возможности диалога "человек - машина". Ничего принципиально нового в них не содержится - это обычные потоковые и балансовые соотношения с учетом некоторых эмпирических соотношений, правдоподобных соображений и причинно-следственных связей. Но этих уравнений много, сама модельная система имеет сложную структуру прямых и обратных связей, а в качестве выходных переменных рассматривается сравнительно небольшое число величин. Что происходит внутри самой модели при проигрывании различных вариантов - толком неизвестно. Для этих моделей (впрочем, как и для самих моделируемых систем) справедлив сформулированный Форрестером "принцип контринтуитивного поведения больших систем". Его сущность состоит в следующем. Наша интуиция основана на столкновении с системами, где связи между причинами и следствиями обычно весьма просты. В больших же системах, структура которых образована длинными цепями причинно-следственных связей, причина и следствие зачастую Разделены в пространстве и времени. И поэтому интуитивные прогнозы о поведении большой системы при применении того или иного воздействия (управления) обычно бывают ошибочными - система ведет себя контринтуитивно. Для оценки ее поведения необходима имитационная модель.

Успех подобного моделирования основывается, по-видимому, на каких-то присущих этим моделям статистических закономерностях, когда неточности и нестрогости в определении индивидуальных взаимозависимостей между отдельными компонентами модели гасятся, а значения выходных переменных можно рассматривать как некоторые термодинамические характеристики всей системы в целом. Но это пока интуитивные соображения.

Существует ли какой-либо критерий, позволяющий оценить "правильность", адекватность построенной модели? Обычно в качестве такого критерия предлагается критерий устойчивости. Считается, что если траектории модельной системы, описывающей некоторую реальную биосистему, устойчивы, то это является одним из необходимых условий правильности построения модели.

Однако требование устойчивости всей биосистемы в целом не обязательно, и оно может быть заменено требованием "иерархической устойчивости", когда нужна устойчивость отдельных блоков системы (а следовательно, и модели), а сами блоки увязываются в систему по принципу временной иерархии.

Возвращаясь к проблеме банка моделей, можно сказать, что выделение достаточно изолированных подсистем и их агрегирование в отдельные блоки должны идти не только по пути естественного выделения биогеоцено-тических систем, не образующих иерархической структуры (биосфера, составленная из различных биогеоценозов, представляет собой мозаичную пространственную одноуровневую структуру), но и по пути выделения иерархических уровней, задаваемых реально существующей иерархией характерных времен различных процессов. В этом случае одному иерархическому уровню могут принадлежать компоненты различных биогеоценозов.

О возможных путях нарушения стабильности биосферы

В этом параграфе мы выскажем несколько гипотез о возможных путях нарушения стабильности биосферы.

Поскольку биосфера представляет собой статистический ансамбль взаимодействующих элементарных структур - БГЦ, то для макроописания ее состояния естественно воспользоваться энтропийными мерами. Самая простая из них - информационная энтропия. Как уже указывалось выше, в экологии она стала почти аксиоматической мерой стабильности сообществ. И, по-видимому, несмотря на все ее недостатки, эта мера более применима ко всей биосфере в целом, чем к отдельным ее элементарным единицам. На это нам позволяет надеяться сравнительно слабая связанность ее элементарных единиц - биогеоценозов.

Согласно энтропийной мере стабильность биосферы возрастает с ростом числа БГЦ (как логарифм их числа). Воздействие человека на биосферу приводит как к уменьшению абсолютного числа БГЦ, так и к обеднению их разнообразия - оба эти процесса ведут к уменьшению информационной энтропии и, как следствие, к уменьшению глобальной стабильности биосферы.

Если учесть, что характерное время замены одного БГЦ другим порядка сотен лет (примерное время формирования лесного биогеоценоза), а характерное время роста человеческой популяции, определяющее скорость роста "энергетической мощи цивилизации, гораздо меньше, то очевидно, что неконтролируемое развитие цивилизации неизбежно должно привести к нарушению стабильности биосферы. Уменьшение энтропии означает, что резко возрастает вероятность больших флюктуации в биосферных процессах, в том числе и таких, которые сделали бы невозможным существование человека как одного из миллионов биологических видов (и это может произойти задолго до потери устойчивости всей биосферы).

Очень грубая модель эволюции любого биологического сообщества (в том числе и живого вещества биосферы в целом) показывает, что на первом этапе, когда виды конкурируют между собой, а общая биомасса возрастает, виды стремятся максимизировать свой репродуктивный потенциал (скорость размножения) и минимизировать средние затраты на конкуренцию, т. е. каждый вид стремится занять свою экологическую нишу и там (насколько ему позволяют ограничения) размножиться. В процессе такой эволюции в биосфере образуется так называемая "горизонтальная" структура, в которой отсутствует иерархия, а трофические цепи имеют наименьшую длину. Именно на этом этале закладывались основные запасы "полезных ископаемых" и формировалась геохимическая среда биосферы, поскольку короткость и простота энергетических цепей обусловливали слабую замкнутость вещественных циклов. На втором этапе необходимо должны были возникнуть более сложные цепи с вертикальной структурой, с большим количеством пар "хищник - жертва", с хорошо развитой системой "разлагателей", позволившей замкнуть биогеохимические циклы. При этом неизбежно должны были возникнуть колебания как численностей отдельных видов, так и общей биомассы. Но чтобы эта система сохранилась, должно было существовать определенное соотношение между массовыми и информационными характеристиками живого вещества биосферы. По-видимому (хотя и очень грубо) живое вещество биосферы можно рассматривать как некоторое биологическое макросообщество и считать, что для него справедливы ранее приведенные соотношения. Если это так, то в процессе эволюции биосферы, не приводящей к исчезновению большого числа видов, должно выполняться неравенство 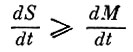где М - суммарная биомасса живого вещества биосферы, S - некоторая информационная характеристика, связанная с числом и обилием биологических видов, с разнообразием живого вещества биосферы. Отсюда следует, что флюктуации живого вещества, которые не разрушают самой системы, должны происходить таким образом, чтобы, например, уменьшение общей биомассы шло не медленнее уменьшения разнообразия биосферы; только при этом не будет происходить уменьшения числа видов.

Этот вывод позволяет сформулировать следующую гипотезу о возможном механизме разрушения биосферной системы человеком. Несмотря на то, что энергетической мощи человеческой цивилизации недостаточно для значительного уменьшения общей биомассы, ее уже хватает для существенного уменьшения видового разнообразия (загрязнение, использование монокультур в агроценозах, урбанизация). В этой ситуации уменьшение разнообразия может происходить более быстрыми темпами, чем уменьшение биомассы (а при интенсификации сельского хозяйства убывание "разнообразия" сопровождается даже ее увеличением). Все это может привести (при нарушении соотношения 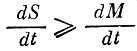) к разрушению современного стационарного состояния биосферы даже при весьма слабых усилиях со стороны человека.

Возможен и другой механизм нарушения устойчивости биосферы, связанный с высказанным выше предположением об иерархической стабилизации биосферных процессов. Вся биосфера Земли есть некоторая иерархическая структура, не обладающая внутренней (структурной) устойчивостью. Стабилизация нижнего уровня обеспечивается следующим уровнем и т. д. вверх по иерархической лестнице. В последнее время энергетическая мощь технологической цивилизации стала сравнима с некоторыми явлениями биосферного масштаба (хотя, как указывалось, эта мощь еще мала по сравнению с энергетикой всей биосферы в целом). Но поскольку характерное время технологических процессов намного меньше времени процессов биосферных, то именно это рассогласование временных масштабов может привести к нарушению стабильности всей биосферы. Вероятно, в настоящее время уже действуют оба этих механизма.

Мы попытались проанализировать подходы к определению такого важного и интуитивно понятного свойства биологических сообществ, как устойчивость или стабильность. Мы не стремились дать набор готовых рецептов, поскольку в большинстве своем изложенные подходы требуют дальнейшего развития. В целом же должно быть ясно, что проблема устойчивости биологических сообществ еще весьма далека от завершения.

Сейчас в этой проблеме можно выделить два основных подхода. С одной стороны, экологи и экспериментаторы, имеющие дело с реальными сообществами, больше тяготеют к оценке устойчивости через различные меры разнообразия. Другой подход, характерный для теоретиков, основывается на исследовании устойчивости математической модели сообщества. Оба этих подхода обладают своими достоинствами и недостатками, но пока не видно пути, который бы их объединил. Может быть, таким мостиком будут идеи и методы системного анализа, в частости, имитационные модели, которые, оставаясь, по существу, математическими моделями, в то же время является почти двойниками реальных систем.