
В поисках третьего измерения (Г. Р. Иваницкий, доктор физико-математических наук. А. С. Куниский, кандидат технических наук)
В поисках третьего измерения
В 1884 г. в Лондоне вышел в свет фантастический роман английского писателя Е. А. Эббота, скрывшего свое имя под псевдонимом Квадрат. Этот роман назывался "Плоский мир" и рассказывал о двумерном мире, населенном существами, которые в зависимости от уровня организации имели различную форму. Наиболее развитые из них представляли собой многоугольники, наименее развитые - отрезки.
Существовали и другие попытки представить себе физический мир с меньшим или большим числом измерений.
Предметы, окружающие нас, трехмерны. Однако изображение этих предметов на сетчатке нашего глаза двумерно. Формирование зрительного образа трехмерного объекта - процесс далеко не простой. В нем участвуют как бессознательные, чисто рефлекторные акты, связанные с оценкой углового положения глаз и степени аккомодации хрусталика, так и логические операции. Как же человек осваивал трехмерный мир, данный ему в ощущениях? Как пытался найти закономерности при изображении его на плоскости, каким путем интерпретировал пространственные объекты, невиданные им ранее, как путем точных вычислений и современной техники научился реконструировать объем по сечениям и проекциям, наконец, как изобрел физические методы, способные создать в отсутствии предмета видимый его эквивалент, его объемный фантом?
Соотношение между зрительным ощущением перспективы и третьим измерением предметов интересовало еще древних греков. Пифагорийцы впервые выдвинули гипотезу об особом флюиде, который испускается глазами и "ощупывает" предметы. Атомисты, напротив, были сторонниками испускания предметами "призраков", которые, попадая в глаза, приносят ощущение формы и глубины. Платон попытался примирить обе теории.
Согласно Платону, от предметов исходит специальный флюид, который встречается со "светом дня", бьющим из наших глаз. Если оба флюида подобны друг другу, то, встречаясь, они "связываются" и глаза получают ощущение глубины видимого. Если же "свет очей" (выражение, сохранившееся от теории Платона) встречается с несхожим флюидом, он гаснет и не дает ощущений.
Несмотря на наивность физической трактовки восприятия, древние греки достигли больших успехов в геометрической оптике. Эвклид старался подчеркнуть геометрический характер оптических изображений. Великий астроном Птолемей не ограничился, как Эвклид, рассмотрением геометрической оптики, он обсуждал физические процессы, лежащие в основе зрения и связанных с ним оптических иллюзий.
Во второй половине первого века вследствие нашествия варваров традиции греков были забыты. Понадобилось десять веков, чтобы человек вновь спросил себя - какова связь между моими ощущениями и реальным миром?
Знаменитый францисканский монах Роджер Бэкон, живший в XIII в., писал о том, что опыт может быть двояким: один посредством внешних ощущений... но этот опыт недостаточен для человека, потому что он не полностью говорит о вещах телесных и ничего не говорит о духовных. Громадную роль в пространственной ориентации играет наше сознание.
В мозгу производится синтез зрительного образа и извлечение информации о его геометрической протяженности и пространственной ориентации из двух в общем-то несовершенных, перевернутых и искривленных шарообразной формой глазного яблока изображений. Чтобы получить информацию о глубине (протяженности предметов), необходимо иметь по крайней мере два плоских изображения, смещенных на некоторый угол.
Направляя оси обоих глаз на данный предмет, мы устанавливаем их под определенным углом, а наш мозг производит оценку этого угла и определяет расстояние в довольно широких пределах. Глаза человека могут поворачиваться в глазных впадинах более чем на 80° в вертикальном и горизонтальном направлениях.
Для пространственного ощущения и оценки расстояния большое значение имеет бессознательное восприятие степени аккомодации хрусталика, фокусирующего на сетчатке изображение различных по удаленности предметов, а также мелкие движения глаз - тремор.
Корректирующая работа мозга при пространственном восприятии чрезвычайно велика. Именно этим объясняется постоянство в восприятии нами размеров предметов в некотором диапазоне расстояний, когда изображения на сетчатке, безусловно, претерпевают изменения. Иногда наблюдается обратное явление. Известно не нашедшее еще объяснения кажущееся увеличение размеров солнца и луны У линии горизонта. Этот парадокс был известен Архимеду.
Стремление человека зафиксировать то, что он видит вокруг себя, склонность к рисованию - одно из самых древних проявлений человеческих способностей. Однако передача глубины, выявление точных пространственных отношений в изобразительном искусстве появились не сразу.
Изображение на сетчатке построено по законам строгой еометРической перспективы (удаленные предметы уменьшаются в размерах). Однако художники, как правило, воспроизводят структуру ретинального изображения на полотне. Древнее египетское искусство вообще не пользовалось приемами передачи глубины. Отсюда вовсе не следует, что египетские художники видели мир плоским. Существует предположение, что отсутствие глубины в картинах египтян связано с какой-то традицией или религиозным запретом. Однако вероятно, что они просто не знали законов перспективы и не умели изображать объемные предметы на плоскости.
Греческие художники при росписи ваз уже пользовались некоторыми примитивными приемами пространственного отображения, в частности сокращением размеров отдаленных деталей. Но строгой геометрической перспективы они не знали.
В древней русской живописи, так же как и в византийской живописи, передача глубины носила своеобразный, необычный для теперешнего зрителя характер, получивший название обратной перспективы. Суть этого метода состояла в увеличении линейных размеров участков изображения с удалением по глубине. Поскольку средневековая живопись основное внимание уделяла изображению "божественных сюжетов", существует мнение, что обратная перспектива была призвана подчеркнуть ирреальность происходящего на картинах, указать на другие физические закономерности, которым подчиняется изображаемый художником "иной мир".
Не отрицая обоснованности такой точки зрения, следует отметить, что имеется и другая, более "земная" гипотеза, связывающая обратную перспективу с эмпирическими поисками средневековым художником закономерностей человеческого восприятия пространства.
Планомерное изучение законов перспективы началось лишь в эпоху Возрождения. Связано это было с развивающимися потребностями архитектуры, с необходимостью представить достоверное изображение объекта в рисунке. Лишь в первой половине XIV в. итальянский художник и архитектор Джотто приступил к решению задачи пространственного отображения предметов на плоскости. Леонардо да Винчи сформулировал закономерности геометрической перспективы, использовал в живописи принципы воздушной перспективы.
Искусство Возрождения в центр мира поставило человека. Изменилось восприятие, а затем и изображение окружающего. Идея конечности и познаваемости Вселенной, хозяином которой является человек, стала главенствующей. Живопись того времени интерпретировала мир по законам геометрической и воздушной перспективы: предметы по мере их удаления равномерно уменьшались, теряли четкость очертаний, приобретали более мягкий, голубоватый тон. Ощущение доступности, познаваемости этого мира, который так удобно наблюдать, смещая взгляд в глубину изображенного пространства,- главные уроки искусства этого времени.
Позднее, в XVII в., изображение глубины становится более изощренным, расширяется горизонтальная протяженность изображаемого пространства. Картины этого периода отличаются четко выраженными пространственными композициями.
Сложно построена композиция картины Рубенса "Поклонение пастухов" (рис. 2). Здесь используется спиральная модель заполнения пространства. Образ маленького Христа находится в центре спирали.

Рис. 2. Пример композиционного построения картины Рубенса 'Поклонение пастухов'
Несмотря на сложность геометрических построений, предметы и вещи, изображаемые на холстах, продолжают оставаться прочными и устойчивыми, а объемные признаки их - неизмененными. Художник изображает (естественно, с учетом масштаба дарования и темперамента) пространство, прежде всего, каким он его видит, и лишь затем - каким знает. Конечно, для этого нужен тренированный глаз, способность увидеть все более краткие мгновения. И тут совершенное оптическое видение заводит в тупик. Поскольку мир пребывает в постоянном движении, пространство оказывается "деформированным" временем. Рушится понятие неизменности, незыблемости.
Импрессионисты предлагают свою трактовку меняющегося мира. Вместо мира, каким мы его видим, они изображают свое впечатление от него. Изображение объективных пространственных закономерностей подменяется гениально схваченными субъективными представлениями о меняющемся мире. Пространственные отношения уступают временным.
Но поиски художественного воплощения пространственных отношений в живописи продолжаются. Гениальный французкий художник Поль Сезанн пытается расширить и углубить задачи живописи. По его представлениям, картина должна вмещать не только результаты наблюдений, но и размышлений. Изображать мир не только таким, каким мы его видим, но в первую очередь, каким его знаем - вот творческая установка Сезанна. Его картины (будь то портрет, пейзаж или натюрморт) - результат длительного, тщательного изучения натуры. "Время и размышления изменяют мало-помалу впечатления от виденного, и, наконец, к нам приходит понимание... Изучение изменяет наше зрение",- писал Сезанн в письме к французскому художнику Э. Бернару. Как это ни парадоксально, но метод Сезанна в живописи близок науке. Главные его этапы - это анализ, систематизация и, наконец, синтез. Динамизм природы Сезанн пытается представить не мгновенным, "стробированным", субъективным впечатлением, как импрессионисты, а путем художественного осознания всей глубины этого процесса. Линейная перспектива уже не может вместить его усложненных представлений о пространственно-временных отношениях окружающего мира. Искусствоведческий анализ полотен Сезанна приводит к мысли о применении Сезанном новых принципов отражения пространства с использованием сфероидной перспективы.
Таким образом, художник дает свою интерпретацию окружающего мира, в том числе и пространственных отношений предметов, расширяя и углубляя наши представления о природе.
Параллельно (так уж всегда получается в истории человечества) исследованием трехмерной организации объектов занимались не только художники, но и ученые. Только здесь это были не виды горных цепей и речных долин, не портреты знаменитостей или близких людей, не груды битой дичи или яблок, это были странные, фантастические, не привычные человеческому глазу изображения далеких планет и микроскопических существ.
Развитие астрономии и микроскопии заставило ученых искать пути трехмерной интерпретации увиденных ими карликов и гигантов. Причем прошлый, приобретенный в обыденной жизни опыт, уже не мог им пригодиться, настолько необычные картины, не похожие на все, что они видели раньше, открывались им. Несовершенные еще приборы они делали сами: Галилей собрал первый телескоп (это был рефрактор с апертурой в 2,5 см), в первых микроскопах Левенгука в качестве линз использовались капельки меда. Но человечество так мало знало тогда, что даже эта примитивная техника сулила великие открытия. Когда Галилей увидел планету Сатурн, то не смог понять, что он видит. Он не мог представить себе, что планета может быть окружена кольцом. Поэтому увиденное он описал как "тройственный объект". Исследование Сатурна продолжил Христиан Гюйгенс. Долго и настойчиво вел Гюйгенс поиски правдоподобной гипотезы. Серии зарисовок планеты, которую ученый наблюдал в разных ракурсах, помогли, наконец, ему прийти к правильному выводу. "Планета окружена,- решил Гюйгенс,- тонким кольцом, нигде не прикреплена к телу планеты".
Непосредственно увидеть кольцо Сатурна в небольшой телескоп, которым пользовался Гюйгенс, да еще с учетом атмосферных флюктуации, весьма затруднительно (об этом свидетельствуют зарисовки Гюйгенса). Поэтому здесь вполне очевидна анализирующая работа мозга tB процессе "видения" трехмерных объектов.
С развитием техники наше зрение получило возможность не только видеть предметы, удаленные на громадные расстояния, но и проникать в глубины материи, наблюдая мельчайшие элементы живой и неживой природы. И поскольку ученые в своих исследованиях всегда находятся в области неизвестного, где прошлый опыт почти всегда бессилен, а будущие знания еще эфемерны, единственное, на что исследователь может надеяться,- это хорошо и точно работающие приборы, надежные, проверенные методики. Именно поэтому годами тщательно шлифовал свои линзы Левенгук, поколения микроскопистов шаг за шагом разрабатывали методы коррекции различного рода искажений (аберраций) микроскопических систем. Именно поэтому в современной микроскопии ведутся работы по точной количественной интерпретации трехмерной организации микроструктур.
* * *
1960 г. Нью-Йорк. Идет Международный конгресс анатомов. В перерыве между заседаниями участники конгресса осматривали город или стремились к прохладным водам океана. Прогулка под парусом вокруг острова Манхэттен - прекрасное развлечение. Судьба случайно свела в одной яхте европейца и американца. Разговорившись, они выяснили, что оба, исследуя срезы трехмерных биологических структур, используют количественные статистическо-геометрические методы, однако эти методы развиты слабо, и из-за этого возникает ряд трудностей с их применением. Короче, собеседники пришли к выводу, что желательно обсудить с коллегами, интересующимися количественным исследованием трехмерных структур, задачи, которые при этом возникают. Объявление в нескольких научных журналах собрало 11-12 мая 1961 г. в горах Фельдберга (Шварцвальд) 11 ученых. Такпоявился термин "стереология" и "Международное стереологическое общество". Американский морфолог Ганс Элиас именно так описывает историю возникновения стереологии - молодой ветви прикладной математики, разрабатывающей методы исследования трехмерной структуры тел, когда известны только их сечения или проекции на плоскость.
Молодая наука нашла почитателей. Стереологическое общество объединило деятелей таких, казалось бы, разных областей знаний, как биология, минералогия, металлография, математика, и даже представителей искусства. В Швейцарии появился журнал "Стереология", "Журнал по микроскопии" Лондонского Королевского общества ввел у себя раздел по стереологии; были выпущены труды конгрессов.
Очевидно, что возникновение стереологии было продиктовано всей предшествующей историей развития науки. Встрече в Нью-Йорке Элиаса и Эвальда Вейбела предшествовали работы наших соотечественников.
19 июля 1932 г. молодой советский математик А. А. Глаголев подал заявку на изобретение, а через два года опубликовал статью о новом микроскопическом анализе горных пород "методом точек". (Спустя 30 лет этот метод станет классическим в стереологии.)
Другой советский специалист С. А. Салтыков в 1938 г. применил метод "точек" в исследовании металлов, затем им были созданы многие другие количественные способы описания структуры. В 1950 г. появилась его книга "Стереометрическая металлография", которая выдержала три издания и была переведена на несколько языков. В 1961 г., через три года после выхода в свет второго издания этой монографии, известный американский металловед, один из президентов стереологического общества Андервуд писал: "Русские нашли эту тему достаточно ценной, чтобы опубликовать целую книгу..."
Весной 1959 г. академик Г. М. Франк в Институте биологической физики АН СССР поставил задачу группе специалистов: "Создать семейство специализированных вычислительных автоматов для исследования геометрии и химического состава биологических микроструктур". В результате сложной работы была создана целая серия приборов, разработаны многие машинные стереологические алгоритмы. Английская фирма "Металле Рисёч" приступила к разработке подобных устройств лишь спустя несколько лет.
Если мы поднимемся на следующий размерный уровень и даже перенесемся в другую область знаний, то тоже столкнемся с необходимостью подобных исследований. О чем может сказать структура обычного града? Она помогает понять механизм образования ледяных "камней". Понять механизм образования - это научиться бороться с градом...
Фотография, сделанная с искусственного спутника Земли, переносит нас в область макроразмеров. Исследовать структуру атмосферы, определять анизотропию воздушных потоков, изучать перемещение воды, вычислять величину и процентное соотношение областей с различным по возрасту складчатым основанием поверхности Земли по аэрофотоснимкам и решать множество других "глобальных" проблем можно с помощью стереологии, которая так удобна при изучении микрообъектов. Разница размеров в 1016 отнюдь не помеха. Методы изучения остаются общими.
Стереология - наука математическая. Теория геометрических вероятностей и аналитическая геометрия составляют ее основу.
Внутреннее строение твердых непрозрачных тел можно исследовать лишь при условии, что изучаемый материал как-то "приоткрыт". Самый простой способ "открыть" его - разделить на куски. Правда, при этом приносится в жертву целостность трехмерной структуры. Однако в плоскости сечения сохраняются "следы" внутреннего строения. По ним и нужно восстановить количественные характеристики компонентов тела.
Для получения "следов" непрозрачных объектов (металл, керамика, горные породы) приготовленные сечения шлифуют, полируют, а иногда и протравливают кислотами. Отсюда название таких препаратов - шлифы. Их можно наблюдать только в отраженном свете. Из полупрозрачных биологических объектов приготавливают тонкие срезы, их наблюдают в проходящем свете. Срез имеет конечную толщину, иногда довольно существенную по сравнению с размером исследуемых структур.
Попробуйте определить длину нарисованной на рис. 3, а линии. Не зная о задаче Бюффона, определить ее окажется довольно сложно. Задача Бюффона была известна еще в 1770 г. Позднее она вошла во все учебники по теории вероятностей. Автором ее был француз Жорж Луи Леклерк Бюффон - директор Ботанического сада в Париже.
Сформулировать эту задачу можно так: если уронить на пол иглу (длиной l, где l равно, например, 10 см), то какова вероятность того, что она упадет на щель между двумя соседними досками (ширина половиц ρ, например, ρ = 20 см)? Положение иглы при каждом бросании можем отмечать по месту нахождения середины иглы на половице и углу, образованному иглой и щелью (рис. 3, б). Изобразим всевозможные положения иглы с помощью диаграммы (рис. 3, в). Высота прямоугольника равна ширине половицы, а на основании откладываются углы в радианах.
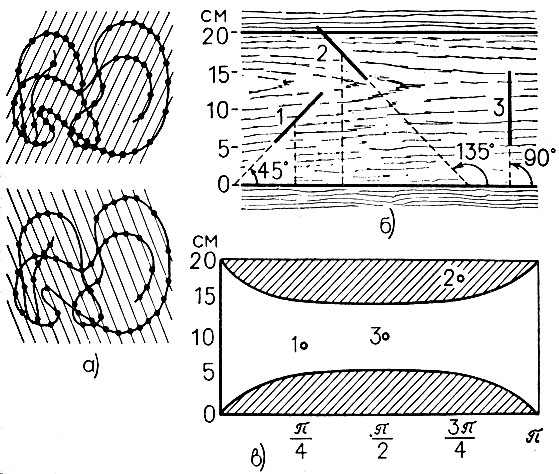
Рис. 3. Задача Бюффона: а - линия, длину которой необходимо определить; б - угловые положения иглы по отношению к половицам; в - поле выборки в задаче Бюффона, точками отмечены три положения иглы по рис. 3,б
Возможные положения иглы составляют множество, которое можно интерпретировать как прямоугольник, площадь которого равна яр. Этот прямоугольник будет "пространством выборок", или "пространством вероятност-ноймеры". Какая же часть площади прямоугольника соответствует в нашем опыте тем положениям иглы, при которых она пересечет щель? Интересующая нас площадь состоит из двух участков внутри прямоугольника с криволинейной границей. Их совместная площадь (ее можно подсчитать путем элементарных тригонометрических выкладок) оказывается равной двум длинам иглы, т. е. 21. Вероятность того, что игла при падении пересечет щель, равна отношению заштрихованной площади на рис. 3,в ко всей площади прямоугольника, или 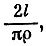 .
.
Если окрашенная игла падала на пол много раз и каждый раз оставляла "след", то в конечном счете следы сольются в линию причудливой формы. Итак, мы бросили иглу N раз (где N - достаточно велико), и она пересекла щель n раз. Отношение n/N равно вероятности пересечения, с другой стороны, вероятность равна 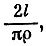 отсюда
отсюда 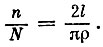 Кроме того, длина линии, составленной из следов иглы при N бросаниях, равна Nl; обозначим ее буквой L. Сделав элементарные преобразования, получим выражение длины линии:
Кроме того, длина линии, составленной из следов иглы при N бросаниях, равна Nl; обозначим ее буквой L. Сделав элементарные преобразования, получим выражение длины линии:
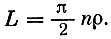 (1)
(1)Как же пользоваться этой формулой? Наложим на линию (рис. 3, а) набор параллельных прямых с расстоянием между ними р (это половицы в задаче Бюффона) и подсчитаем число пересечений п прямых с линией, далее, по формуле (1) найдем длину линии.
Следует помнить, что все положения иглы на полу должны быть в равной мере правдоподобны, а на практике могут встретиться кривые, которые имеют неслучайную ориентацию элементарных отрезков, например вытянутые фигуры. Чтобы в этом случае можно было применить метод Бюффона, нужно несколько раз наложить на кривую набор параллельных линий (рис. 3, а), а результат усреднить.
Мы рассмотрели элементарный случай из геометрических вероятностей - определение длины изогнутой линии. Однако подобные рассуждения позволяют решать задачи по определению длины перепутанных волокон в пространстве. Примером таких волокон могут служить корни растений, капиллярная кровеносная сеть и т. д.
Как и в любом разделе прикладной математики, в стереологии часто идут на упрощения, без которых невозможно обойтись при замене реального объекта его математической моделью. Многие стереологические методы предполагают "однородность" структуры в том смысле, что она должна быть составлена из геометрических тел одного типа, например только из шаров (рис. 4) или из эллипсоидальных фигур. Размеры их могут быть различны.
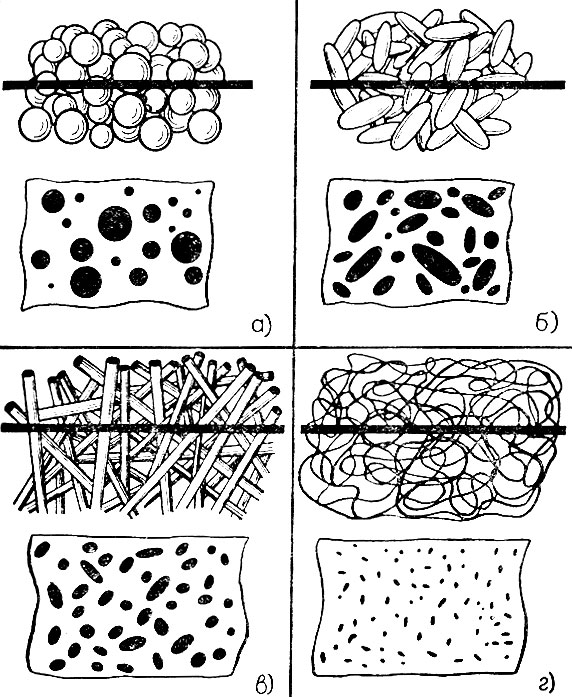
Рис. 4. Несколько типичных задач, которые решаются с помощью стереологических методов: а) Померив распределение сечений шаров по диаметрам, определить распределение самих шаров по их диаметрам. б) По сечениям случайно ориентированных эллипсоидов вращения сигарообразной или дискообразной формы вычислить коэффициент эллиптичности, число эллипсоидов в единице объема, среднюю длину осей, отклонение истинных длин от среднего значения, средний объем эллипсоида й общий объем всех эллипсоидов. в) По эллиптичности сечений определить тип рассеченных тел - круговые цилиндры, плоские диски или волокна. г) Вычислить для тонких случайно ориентированных волокон их удельную длину на единицу объема
Как же сделать формулы, выведенные для идеализированных однородных структур, применимыми к реальным препаратам? Существует, во-первых, избирательная обработка, например окраска. Этот путь широко применяется в биологии: покрасьте только ядра клеток, и вы получите идеализированный препарат, составленный из шаров или эллипсоидов; наполните кровеносные сосуды исследуемой ткани тушью - перед вами препарат, состоящий из цилиндров или волокон. Второй путь состоит в том, что сам исследователь или анализирующее автоматическое устройство выбирает фигуры одного типа, производя их измерение.
В подписях под рис. 4 сформулированы некоторые типичные задачи, которые решаются с помощью стереоло-гических методов.
Сегодня решено свыше двух десятков аналогичных задач. Получены формулы для количественного описания ориентации структур, для определения формы включений, для исследования топологических характеристик трехмерных структур и многие другие. Формулы стереологии существенно облегчают количественное исследование трехмерных структур. Правда, порой они вызывают у специалистов недоверие из-за своей простоты. В этом смысле примечательна история, которую рассказал профессор С. М. Блинков. Лет десять назад он совместно с одним математиком опубликовал в "Докладах Академии наук" формулу для определения удельной длины кровеносных сосудов в мозгу по их следам на срезах. Это было обобщение формулы Бюффона на трехмерный случай, когда ориентация кривой в пространстве имеет предпочтительное направление. Через три года профессор получил письмо от немецких морфологов. Они писали, что "проверили" применимость формулы: взяли длинную капроновую нить известной длины и свили ее в клубок, затем, растянув клубок в определенном направлении, залили его парафином, приготовили срезы и посчитали по формуле удельную длину нити. Расхождение не превышало нескольких процентов. Отсюда они сделали заключение, что формулу можно рекомендовать для морфологических исследований.
В 60-х годах в журналах часто встречались такого рода проверки стереологических положений. Впрочем, в последнее время такие проверки появляются все реже и реже.
С помощью стереологических методов решены многие ррактические задачи по определению параметров строения тел, например, но изменению фазовой структуры металлов, ло вычислению удельной поверхности коры головного мозга животных и т. д.
Следует указать, что при выводе стереологических формул необходимо ввести систему координат. Однако выбор системы выделяет в пространстве некоторые направления, соответствующие осям координат, что противоречит "изотропности и однородности" пространства, т. е. равноправности всех его направлений. Поэтому практический интерес могут представлять параметры, которые не зависят от выбора направления осей. К таким параметрам относятся: линейные размеры, площади и объемы структурных элементов. Они обладают пятью важными свойствами: инвариантны относительно движений; аддитивны (например, при разложении тела на части сумма объемов частей равна объему тела); не могут принимать отрицательных значений; при равномерном растяжении тела в r раз они увеличиваются в гn, где n - размерность пространства (n = 1 для прямой, п = 2 для плоскости, n = 3 для трехмерного пространства); инвариантны относительно равносоставленности (например, объемы двух тел, составленных из одних и тех же частей, равны, хотя форма их может быть различна).
Из этих свойств вытекают как достоинства, так и недостатки использования этих параметров описания структур. Для определения количественных параметров нам необходимо оперировать сразу со всей совокупностью структурных элементов. Плоскость наблюдения (плоскость среза) в этом случае проходит случайным образом и не зависит от структуры объекта. При решении указанных задач математик сталкивается с интегральными уравнениями такого вида:
g(p) = ∫ K (pQ) G(Q) dQ, (2)
где g(p) - распределение параметра, измеряемого на срезе, G(Q) - распределение параметра в объеме, K(pQ) - некоторая функция, зависящая от вида структуры, ее называют ядром уравнения, А - область интегрирования. Подобные уравнения имеют однозначное решение только при определенных видах функции K(pQ). Например, Уравнение, связывающее распределение сечений шаров в срезе с распределением их диаметров в объеме (рис. 4, а), имеет вид:
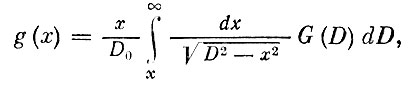 (3)
(3)
где g (х) - функция распределения сечений по радиусам (измеряется в эксперименте), D0- средний диаметр шара, выбранный наудачу; G(D) - функция распределения шаров по диаметрам (вычисляется). Ядро этого уравнения есть 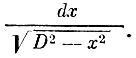 После подстановок уравнение (3) можно привести к уравнению вида
После подстановок уравнение (3) можно привести к уравнению вида
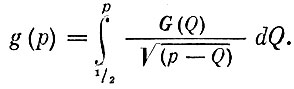
Такое уравнение известно под названием интегрального уравнения Абеля (Нильс Абель - норвежский математик начала XIX в.). Решением его будет выражение
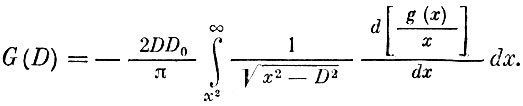
(4)
Однако мало найти математическое решение уравнения, необходимо, чтобы оно было корректным. Здесь мы сталкиваемся с проблемой "корректности обратных задач". Обратными задачами в широком смысле этого слова называются задачи, которые решаются в обратном порядке причинно-следственных отношений (по следствию необходимо выяснить причину). Почти все научные исследования - это решения обратных задач; наблюдается эффект, производимый изучаемой системой (следствие), а восстанавливается ее строение (причина). Параметры сечений структур на срезах - это следствие нарезания, а по ним необходимо восстановить параметры трехмерной структуры. Обратным задачам уделяли много внимания крупные математики прошлого (Анри Пуанкаре, Жак Адамар), этой проблемой интенсивно занимаются и сегодня. Обратим внимание на особенности таких задач. Они часто не имеют решения, т. е. в результатах наших наблюдений может не оказаться необходимой информации (другими словами, эксперимент поставлен неверно). Иногда из-за неоднородности структуры возникает неоднозначность решения; и наконец, третья особенность - некорректность задач, т. е. большая чувствительность к ошибки. Если функция g (x) измеряется с ошибкой (а при измерениях погрешность всегда существует), то вычисляемая функция G (D) может сильно отличаться от истинного значения.
Механизм такой слабой помехозащищенности очевиден. Параметры объемной структуры вычисляются как разности близких величин, измеряемых в сечениях (обратите внимание на второй сомножитель в уравнении (4) - там стоит производная от функции g (x)). Способ уменьшить ошибку один - значительно увеличивать статистику измерений при определении функции g (x).
Резюмируя, следует подчеркнуть, что при выводе стереологических формул встают два препятствия: ошибка при построении вероятностной модели структуры и сложность решения обратных задач.
Оптический микроскоп исчерпал свои возможности в середине XX в. Для повышения его разрешения ученые решили использовать излучение с более короткой длиной волны. При исследовании трехмерных объектов излучение, дифрагированное на внутренней структуре объекта, создает в дальней дифракционной зоне поле, распределение амплитуд и фаз в котором связано с распределением плотности в структуре объекта преобразованием Фурье. Эти строгие количественные соотношения между структурой объекта и рассеянным им излучением навели ученых на мысль о возможности расчетного формирования изображения. Для этого используются данные о распределении амплитуд и фаз в обратном пространстве.
Круг задач такого плана довольно распространен в структурных исследованиях и получил название обратных дифракционных задач. Возникают они в тех случаях, например, когда по условиям эксперимента невозможно сформировать увеличенное изображение объекта. Так, из-за высокой проникающей способности рентгеновских лучей трудно изготовить линзы, которые могли бы обеспечить формирование в этом диапазоне изображения. Однако зарегистрировать распределение поля в дальней дифракционной зоне можно, так как для этого не требуется никакой "оптики". Выполнив обратное преобразование Фурье от распределения амплитуд и фаз в обратном пространстве, можно расчетным путем восстановить изображение структуры. На этой идее основывается такое мощное направление исследований, как рентгеноструктурный анализ. Этот метод, предложенный Лауэ и Книппингом в 1912 г., нашел продолжение в известных работах отца и сына Брэггов и других ученых.
Одна из основных сложностей рентгеноструктурно-го анализа состоит в том, что детекторы, используемые для регистрации рассеянного излучения,- квадратичны (т. е. регистрируют лишь интенсивности - квадраты амплитуд и не регистрируют фаз). Для расчетного восстановления структуры необходимо знать распределения не только амплитуд, но и фаз в обратном пространстве. Поэтому фазовая проблема считается одной из главных в рентгеноструктурном анализе. Решить ее удается пока далеко не для всех объектов, и методы решения выглядят весьма трудоемкими.
Электронный микроскоп, в котором объект "освещается" пучком электронов, также повышает разрешение по сравнению с оптическим микроскопом, но появились и новые проблемы. Электромагнитные линзы, формирующие изображение объекта, оказались весьма несовершенными. Эквивалентное по качеству изображение в оптическом диапазоне могла бы создать обыкновенная дождевая капля. Сильные и, к сожалению, принципиально неустранимые сферические аберрации размывают электронно-микроскопическое изображение. Единственная возможность ослабить как-то искажающее действие аберраций состоит в использовании лишь центральной зоны электромагнитной линзы, другими словами, в уменьшении ее апертуры. Изображение при этом становится более четким, однако оно теряет при этом другую, не менее важную характеристику - глубину.
Трехмерная структура объекта представляется на электронно-микроскопическом снимке в виде плоской проекции. А информация о третьем измерении молекулярных структур, исследование которых ведется с помощью электронного микроскопа, представляется очень важной. Ведь функциональные свойства важнейших компонентой клетки - белков определяются во многом расположением атомов молекулы в пространстве. Конфигурация, которую приобретает последовательность аминокислот, формирующая полипептидную цепь, связана с тем, что молекула стремится принять форму, при которой ее свободная энергия минимальна. Основные жизненные процессы, такие, как дыхание, движение, связаны с изменением пространственной организации отдельных компонентов белковых молекул.
Размеры объектов, представляющих интерес для биологии, составляют десятки, сотни ангстрем. Глубина же фокуса электронного микроскопа за счет ограниченной апертуры значительно больше (примерно две тысячи ангстрем). В результате небольшие, но достаточно сложные объемные образования, наблюдаемые в электронном микроскопе, представляются в виде проекции трехмерной структуры на плоскость. Третье измерение оказывается утраченным за счет суммирования плотности в направлении распространения электронного пучка. В этом и состоит одна из основных сложностей в исследовании пространственной организации молекулярных структур с помощью электронного микроскопа.
До сих пор трехмерная интерпретация электронно-микроскопических изображений является наиболее уязвимым местом электронно-микроскопического анализа и во многих случаях базируется на интуиции и опыте исследователя. Часто прибегают к получению снимков структуры в различных ориентациях. Известно, что такой прием облегчает получение представления о пространственной организации объекта. Напомним хотя бы приведенную выше историю о том, как Христиан Гюйгенс открыл кольцо Сатурна, наблюдая за этой планетой в различные моменты времени, когда с Земли она видна в различных ориентациях. Можно ли использовать точные количественные методы для извлечения информации о третьем измерении, достоверно реконструировать трехмерную структуру? Оказывается, можно.
В последние годы в Англии, Советском Союзе и США появились описания различных методов точного, количественного восстановления трехмерной структуры по ее электронно-микроскопическим снимкам. Для этого необходимы электронно-микроскопические снимки объекта, снятого в разных ориентациях. Точно промеренные микроденситометром данные о степени почернения отдельных снимков вводятся в вычислительную машину, которая Рассчитывает распределение электронной плотности в ечениях структуры, совпадавших с направлением просвечивания.
Идею трехмерной реконструкции молекулярных структур по набору электронно-микроскопических изображений высказали Клуг и Де Розье в 1968 г. в Кембридже (Англия). Не случайно эта работа выполнена именно в Кембридже, месте, широко известном среди специалистов глубокими и оригинальными исследованиями по определению пространственной организации молекулярных структур. Позднее выяснилось, что в 1956 г. Брейсвеллом в Австралийском физическом журнале было предложено решение подобной задачи в радиоастрономии. В частности, им был рассмотрен вопрос о восстановлении распределения яркости в радиоисточниках по их проекциям, полученным под различными углами за счет вращения Земли.
Близость в формальном описании объектов разной природы привела ученых к одним и тем же решениям задачи восстановления их объемной организации.
Заслуга Клуга и Де Розье как раз и состояла в том, что они вспомнили об обратном пространстве и предложили использовать расчетные методы восстановления в электронной микроскопии. В Кембридже рассуждали примерно так: большая глубина фокуса, естественно,- недостаток электронного микроскопа, но исправить его, изменив конструкцию электронного микроскопа, сейчас вряд ли возможно. Нельзя ли из таких электронно-микроскопических изображений, какие они есть, извлечь все же информацию о третьем измерении структуры? Оказалось, можно. Причем недостаток может быть обращен на пользу. Выяснилось, что в электронном микроскопе формируется изображение, которое при определенных условиях может рассматриваться как проекция трехмерной структуры на плоскость, т. е. как интеграл от функции, описывающей распределение плотности в объеме по одной из переменных, совпадающей с направлением просвечивания. Если распределение плотности в трехмерном объекте описывается функцией ρ (х, у, z), то изображения, формируемые при разных направлениях просвечивания, представляют собой двумерные проекции трехмерной структуры на плоскость. Причем распределение плотности в проекциях пропорционально всякий раз интегралу от трехмерной функции. Так, проекция σ (х, у) вдоль направления z пропорциональна выражению ∫ ρ (x, у, z) dz. Преобразование Фурье от такой проекции есть центральное сечение трехмерного обратного пространства - Ф (X, У, О). Поскольку распределение плотности в проекции известно, а преобразование Фурье выполняется расчетным путем, то в центральном сечении обратного пространства будут известны и амплитуды, и фазы. Если теперь объект в электронном микроскопе повернуть под небольшим углом, то электронно-микроскопическое изображение будет представлять собой проекцию той же структуры, но снятую в другой ориентации. Преобразование Фурье такой проекции опять будет центральным сечением обратного пространства, но с другим угловым положением. Некоторый набор проекций объекта, снятых в разных ракурсах, при переходе в обратное пространство даст набор центральных сечений. Таким образом, имея достаточное количество проекций, можно заполнить обратное пространство пересекающимися по одной прямой плоскостями. Произведя интерполяцию между ними и выполнив обратное преобразование Фурье, можно восстановить распределение плотности в сечениях объекта, плоскость которых совпадает с направлением просвечивания. Другими словами, можно увидеть внутреннюю структуру объекта, которую не удается увидеть на электронно-микроскопических снимках, но информация о которой в закодированной форме присутствует в проекциях объекта. Одна проекция симметричного объекта уже содержит информацию, необходимую для восстановления.
Исследование таких спиральных структур, как волокна биополимеров, молекулы которых имеют нитевидную форму и образуют фибриллярные структуры сократительных белков (актина, миозина) и их комплексов, а также простейших структур, способных к сокращению, типа чехлов бактериофагов, представляют исключительный интерес в биологии.
В принципе возможна реконструкция трехмерной структуры по проекциям ибез перехода в обратное пространство. Очень много для развития подобных методов сделал советский ученый Б. К. Вайнштейн. Одно из возможных решений состоит в том, что каждая из проекций в дискретном представлении может рассматриваться как сумма значений плотности в одном из узлов решетки, на которой ведется восстановление.
Таким образом, могут быть составлены линейные уравнения вид
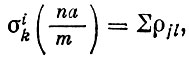
где a/m - шаг дискретизации, с числом неизвестных в каждом уравнении m. В общем случае, если имеется р проекций (i = р), то число известных - рm, а неизвестных значений - рjl - m2. Условие однозначного определения каждого из значений рjl (т. е. реконструкция одного из сечений структуры) - рm≥m2 или р ≥ m.
В реальном пространстве работает и другой метод трехмерной реконструкции, получивший название метода восстановления обратным проектированием, или синтезом проектирующих функций. Идея метода иллюстрируется на рис. 5, где показано двумерное восстановление функции ρ (х, у) (в полярных координатах ρ (r Ф) из последовательности N проекций σψ (x), расположенных через равные углы 2π/N. Для каждой точки в структуре все проектируемые плотности σψ [х' = rcos (Ф - ψ)] суммируются.
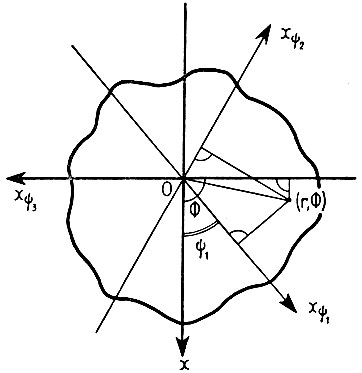
Рис. 5. Восстановление обратным проектированием
Можно показать, что даже при бесконечном числе проекций метод реконструкции обратным проектированием не будет восстанавливать истинной плотности ρ (r, Ф), а будет реконструировать ρ (r, Ф), свернутую с 1/r, где r - радиус объекта.
Причина, по которой метод обратного проектирования не может дать действительной реконструкции, состоит в том, что выборка преобразования объекта производится в неправильной пропорции для различных радиусов в обратном пространстве.
Модификацию описанного выше способа с целью устранения присущих ему ошибок предложили член-корреспондент АН СССР Б. К. Вайнштейн (модифицированный синтез проектирующих функций) и индийский ученый Рамачандран (метод свертки). Суть модификации сводится к следующему. Если выборочную функцию изменить так, чтобы она меняла свое значение в соответствии с радиусом обратного пространства, то можно осуществить верную реконструкцию, точность которой ограничена лишь тем, что используется конечное число проекций.
Оценка точности восстановления будет зависеть от числа проекций, характера вычислительных операций (степени усреднения, вида интерполяции) и достоверности данных при экспериментальном определении проекций.
Для расчетов на вычислительной машине распределения электронной плотности в сечениях структур со спиральной симметрией необходимо знать основные параметры спирали: заходность, период, число групп в обороте и др. Эти параметры могут быть определены при переходе опять-таки в обратное пространство. На этот раз используются не расчетные методы, а дифракционные двумерные спектры, полученные в когерентной оптической системе. В качестве примера можно привести восстановление пространственной организации отростка бактериофага Н-17, одной из самых элементарных сократительных структур, известных в природе. На рис. 6 показан дифракционный спектр отростка. Распределение оптической плотности в электронно-микроскопическом изображении структуры - исходный материал для машинной реконструкции - измеряется с помощью автоматического сканирующего денситометра, определяющего степень почернения фотопластинки.
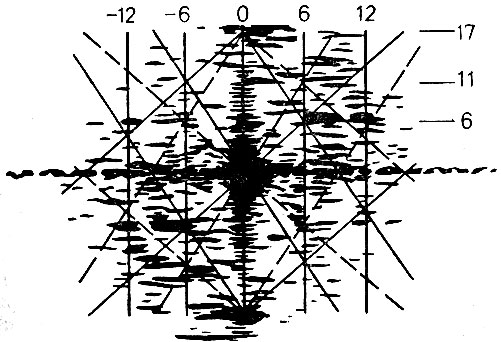
Рис. 6. Дифракционный спектр отростка бактериофага Н-17. Bacillus mycoides
* * *
С попыткой устранить влияние сферических аберраций в электронном микроскопе связано другое крупнейшее открытие в науке XX в.- открытие голографии.
Идея голографии была высказана Д. Табором в одном из номеров журнала "Нейчур" за 1947 г. Она касалась возможностей компенсации сферических аберраций в электронном микроскопе и состояла в двухступенчатом процессе регистрации изображения. На первом этапе фиксировалось распределение амплитуд и фаз дифрагированного излучения, а на втором осуществлялось восстановление волнового фронта в оптическом диапазоне, где и производилась коррекция аберраций. Регистрация фаз оказалась возможной за счет интерференции рассеянного объектом излучения с когерентным фоном. Несмотря на то что голограмма фиксировалась на фотопластинках, регистрирующих лишь интенсивности, за счет предложенной Габором интерференции с фоном, записанное распределение интенсивности все же сохраняло информацию о фазах.
Работа Габора была почти забыта до начала 60-х годов, когда изобретение лазера дало мощный толчок развитию голографии. Поразительный эффект трехмерности при восстановлении голограмм объемных объектов, впервые продемонстрированный Э. Лейтом и Ю. Упатниексом, был обязан высокой степени когерентности источника освещения. То, что пытались сделать импрессионисты в искусстве - остановить мгновение, удалось физике - голограмма останавливала ("замораживала", как часто говорят) волновой фронт, идущий от предмета, а затем в нужный момент времени, уже в отсутствии предмета, помещенная в когерентный пучок, вновь восстанавливала его. Этот волновой фронт и создавал объемное изображение предмета, его двойник.
Вот как Э. Лейт описывает первое необычайное впечатление от рассматривания голограммы: "Мы испытывали сильное волнение, хотя результаты были нам известны... Сама голограмма не производила впечатления, она представляла собой лишь наложения интерференционных картин, в котором не было видно никакого смысла, однако лишь только мы поместили ее в пучок когерентного света, появилось изображение. Результат был как раз таким, как мы ожидали, но его физическое осуществление было впечатляющим. Изображение - без видимого объекта! Наши коллеги были озадачены, отнесясь к этому с некоторым подозрением".
Голограммы диффузно отражающих трехмерных объектов обладают некоторыми уникальными свойствами, присущими лишь этому методу регистрации изображений. Они способны нелокально регистрировать информацию. Другими словами, по фрагменту, например осколку голограммы, можно восстановить целое изображение. В последнее время в связи с этим интенсивно обсуждается вопрос о формальной близости голографического процесса и явлений, связанных с ассоциативными формами запоминания.
В то время как мнимое изображение, восстановленное с голограммы, является точной объемной копией исходного предмета, действительное изображение обладает интересным свойством псевдоскопичности. Это изображение инвертировано по глубине и создает совершенно непривычные зрительные эффекты, когда более отдаленные участки изображения заслоняют собой более близкие его части при изменении направления наблюдения. Псевдо-рукописность действительного изображения может быть устранена, если на стадии регистрации голограммы использовать линзу, которая делает волну, распространяющуюся от объекта, сходящейся.
В 1962 г. советский физик Ю. Н. Денисюк предложил оригинальный метод голографической записи волновых фронтов в толстослойных эмульсиях. Предметная и опорная волна падает на эмульсию с противоположных сторон, образуя систему стоячих волн. Восстановление изображений с таких голограмм возможно вести в белом свете.
Сейчас даже трудно перечислить все приложения, которые нашла голография в научных исследованиях. Задача казавшаяся фантастической до появления голографии, сейчас может быть решена сравнительно простым техническим средством. Характерный пример - определение размеров частиц в выхлопных газах из сопла, движущихся со скоростью, вдвое превышающей скорость звука. Регистрация голограммы с помощью рубинового лазера с длительностью импульсов 20-30 нc, а затем микроскопический анализ трехмерного изображения потока, восстановленного с голограммы, с последовательной фокусировкой на различных частицах - вот решение такой проблемы. Подобными же методами оказалось возможным зарегистрировать всех инфузорий в полутораметровой толще мутной воды или же насекомых в метровом столбе воздуха. Американскими исследователями Ноксом и Бруксом был снят даже голографический фильм, воспроизводящий полет одного москита. Голограммы могут фиксироваться не только в световом диапазоне, но и в области ультразвука и СВЧ. Это открыло интересные возможности в медицинских исследованиях и в радиолокации. Вычислительная техника дает возможность рассчитать дифракционные картины от несуществующих объектов. Переведенные соответствующим образом на пластинки, эти машинные голограммы могут восстановить объемные изображения объектов, существующих только гипотетически. Интенсивно ведутся работы по созданию голографического кино и телевидения. Здесь, правда, имеются определенные сложности, но существуют и достижения. К числу их следует отнести получение трехмерных портретов человека с помощью импульсных лазеров, обладающих большой длиной когерентности (в несколько метров). Так изготовлен, например, голографический портрет Дениса Габора, демонстрировавшийся перед его Нобелевской лекцией. И наконец, появляются связи между детищем современной техники и изобразительным искусством.
Голография сможет сделать широкодоступными для наблюдения уникальные произведения искусства. Например, проводятся подготовительные работы по голографированию ценнейших экспонатов Эрмитажа.
Такая работа чрезвычайно важна и в области сохранения информации о памятниках культуры, подверженных разрушению. Так, по сведениям журнала "Сайенс", 35% произведений искусства в Венеции находятся под угрозой разрушения. Был произведен эксперимент по голографированию некоторых произведений венецианской скульптуры. Причем рассматривание восстановленных с голограмм изображений, по мнению специалистов, немногим уступало эстетическому впечатлению от оригинала. В будущем вэзможно создание голограммного хранилища известных произведений древнего искусства.
Иллюстрации зависимости 'структура - время'
Эффектная зрелищность голографических изображений используется часто на Западе в целях рекламы. Скандально известный сюрреалист Сальватор Дали заявил о создании им трехмерного голографического портрета рок-звезды Элиса Купера, для устрашения зрителя выступающего на сцене то в обличье дьявола, то в саване покойника.
В ноябре 1972 г. на Пятой авеню Нью-Йорка в течение нескольких часов движение было остановлено огромной толпой, рассматривавшей женскую руку, протягивающую из полутьмы витрины бриллиантовое ожерелье. "Таинственное" изображение восстанавливалось мощным лазером с голограммы изготовленной фирмой "Мак-Доннел Дуглас Электронике". Эффект объемности был настолько поразительным, что какой-то из нервных зрителей в конце концов разбил зонтиком витрину, заявив, что это работа дьявола.
Есть и еще один аспект в исследовании пространственной организации объектов окружающего нас мира.
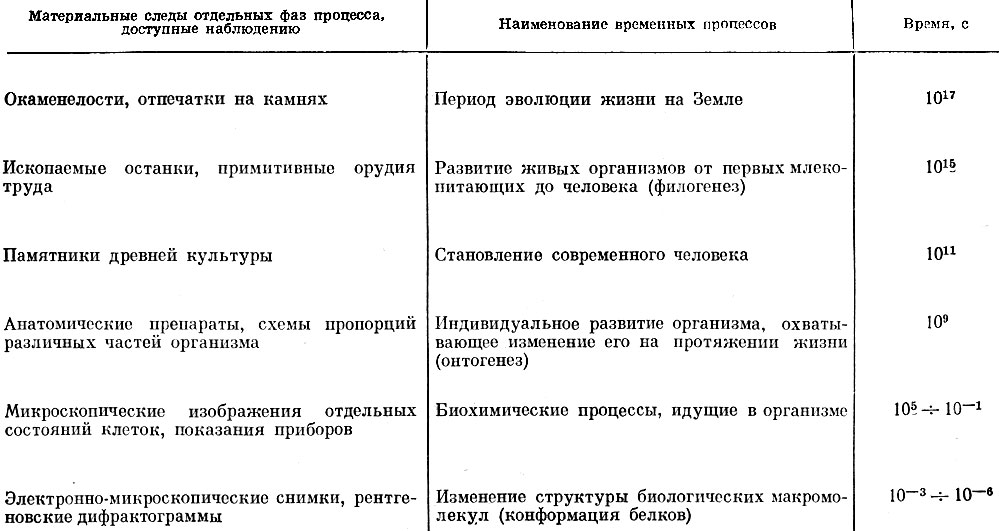
Препарируя объекты трехмерного мира, мы замечаем, что в строении их присутствует четвертое измерение - время. Геологические пласты земной коры, годовые кольца на срезе дерева, длина витков спирали на панцире улитки - все это вехи времени.
Однако секунды и минуты, часы и годы в растущей и сворачивающейся структуре в трехмерном пространстве превращаются в сантиметры и угловые градусы. Конечно, не всегда пропорциональность между единицей времени и единицей длины линейная. Появляется понятие "относительного времени", запечатленного в структуре. При изучении определенных этапов развития структуры время представляется прерывным (квантованным). Смена дня и ночи, времен года и солнечных циклов оставляет "зарубки" на структуре объектов. Для изучения сложных процессов необходимо препарировать трехмерное пространство и искать в нем автографы времени (см. табл.).
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'