Математика и описательные науки (А. А. Дородницын, академик)

Математика и описательные науки

Говоря об описательных науках, мы имеем в виду деление наук на две группы: точные науки и описательные.

Термин "точная наука" возник, по-видимому, из наивной веры физиков прошлых времен, полагавших, что открываемые ими закономерности являются абсолютно точными. Правильнее под точной наукой понимать такую, которая обладает средствами предвидеть с практически достаточной точностью развитие процессов, изучаемых данной наукой, на достаточно длительный (снова-таки по практическим соображениям) промежуток времени. Или, чтобы не связываться непременно с развитием во времени: предвидеть достаточно точно свойства и соотношения изучаемых объектов по некоторой частичной исходной информации о них.

Описательные науки представляют собой, по существу, перечень фактов об изучаемых ими объектах и процессах, иногда не связанных между собой, чаще связанных некоторыми качественными соотношениями. Хотя не исключены и разрозненные количественные (как правило, эмпирические) связи.

К точным наукам относят сейчас математику и науки физического цикла (механику, термодинамику, электродинамику, квантовую механику, химическую кинетику и др.).

Все остальные науки в большей или меньшей степени пока что относятся к классу описательных.

Я сказал "пока что" потому, что "точность", или "описательность", не есть свойство данной науки, а лишь характеристика этапа ее развития. Все науки когда-то были описательными, включая даже математику. Геометрия, например, в древние времена представляла собой "сборник рецептов", иногда чисто эмпирических. Скажем, у древних египтян для вычисления площади круга рекомендовалось брать ³/₄ площади описанного квадрата. Механика стала точной наукой примерно 300 лет назад, а большинство разделов физики - лишь в XIX в.

Создание электронных вычислительных машин, повысивших в миллионы раз вычислительные возможности человека, стимулирует попытки применения математических методов в описательных науках, например в экономике, биологии, медицине, геологии, и сейчас мы находимся, по-видимому, на этапе превращения экономики в точную науку.

Чтобы уяснить себе, какую роль смогут сыграть математические методы, опирающиеся на всю мощь современной вычислительной техники, в описательных науках необходимо проанализировать процесс развития наук. Я попытаюсь изложить, как этот процесс мне представляется.

Развитие науки происходит по ряду параллельных русел. Различные русла начинаются в разное время, но раз Начавшись всегда продолжаются.

Начинается каждая наука с целеустремленного накопления информации об объектах, которые она изучает (слово "объект" здесь применяется в общем смысле, это может быть явление, понятие или материальный объект в прямом смысле слова). Конечно, человек, да и любое животное всегда стихийно, подсознательно, накапливает информацию (верную или неверную) об окружающих его объектах. Научное накопление информации отличается от стихийного не только своей правильностью (наука тоже может ошибаться), а именно целеустремленностью: накопление производится сознательно для того, чтобы понять сущность объектов и связи между ними.

Одновременно или почти одновременно с накоплением информации начинается процесс ее упорядочивания - классификация объектов. Конечно, человек, а также и животные, начал классифицировать окружающие его объекты без всякой науки. Но эта наивная и я бы сказал "потребительская" классификация является часто субъективной-по признаку отношения объекта к человеку. Научная классификация отличается от наивной своей целеустремленностью - облегчить анализ изучаемых объектов (хотя и она иногда может быть субъективной).

Эти два русла - накопления и упорядочивания информации находятся в постоянном взаимодействии -' они связаны процессом идентификации. Каждый новый объект анализируется: принадлежит ли он к уже установленным классификационным группам или открывает новую группу, или, наконец, по мере накопления информации указывает на необходимость перестройки системы классификации.

Третьим руслом в развитии науки является установление связей и соотношений (качественных или количественных) между объектами. Эти связи обнаруживаются в результате постоянного анализа накапливаемой и упорядоченной информации. Общность связей, таким образом, устанавливается эмпирически (а не доказывается).

Эти три русла характеризуют "описательный" период развития науки. Он может длиться тысячелетиями, пока не наступает "переход количества в качество" (который тоже может длиться весьма долго). Количество накопленных сведении о связях и соотношениях между объектами позволяет выделить определяющие, из которых другие могут быть выведены уже дедуктивно.

Переход начинается с попыток построения математических моделей процессов, изучаемых данной наукой. Но математическая модель может строиться на каких-то количественно строго определенных величинах. Таким образом, необходимо произвести выделение существенных исследуемого явления и сопоставление им количественно строго определенных величин. Так появляются два новых русла в развитии науки - установление величин и математическое моделирование. Они непрерывно связаны с третьим руслом - установлением связей и соотношений, и начало точного периода можно отнести к тому времени, когда выбранные величины и математические модели достаточно полно и точно согласуются с накопленными в третьем русле фактами.

Хочется особенно подчеркнуть важность этапа "установления величин". Мы можем проследить его на примере развития точных наук. В механике "законы" статики были установлены еще Архимедом. Но потребовалось время от Архимеда до Ньютона пока точной наукой стала динамика.

Законы Ньютона поражают своей простотой. Несомненно, что математического таланта Архимеда вполне было достаточно, чтобы сформулировать подобные законы. 2000 лет ушло на "установление величины", на то, что силу нужно связывать с ускорением, а не со скоростью, как пытались это сделать до Ньютона (или во всяком случае до Галилея).

"Законы" Ньютона оказались поразительно точной математической моделью механических движений. Лишь через двести лет стали обнаруживаться явления, и в третьем русле появились соотношения, которые потребовали уточнения математической модели Ньютона и замены ее моделью релятивистской механики.

Очень характерный пример важности и в то же время сложности установления величин дает квантовая механика. Определяющая величина здесь волновая функция if), через нее выражаются все наглядные физические величины. Но что есть она сама? Все попытки приписать ей прямой, наглядной физический смысл являются весьма натянутыми.

Не только квантовая механика, классическая физика также дает примеры ненаглядности определяющих величин. Потенциал, энтропия, количество электричества? Все они не являлись непосредственно наблюдаемыми величинами. Если, скажем, сейчас мы можем связать количество электричества непосредственно с числом избыточных или недостающих электронов, то во времена Кулона с количеством электричества были связаны весьма туманные представления. Необходимость введения этой величины вытекала из математической обработки накопленных количественных наблюдений.

То же относится и к энтропии, которую и сейчас определить наглядно не удается, она "вытекала" из уравнении термодинамики.

На приводимой схеме (рис. 1) иллюстрируются изложенные выше соображения о развитии наук. Попробуем проанализировать, где же в этой схеме развития науки математические методы могут дать существенный эффект? Говоря о математических методах, я не имею в виду узкое значение этого слова (аналитические методы), а говорю о них в смысле строго формализованных правил обработки информации.Тогда ответом на поставленный вопрос будет: везде.

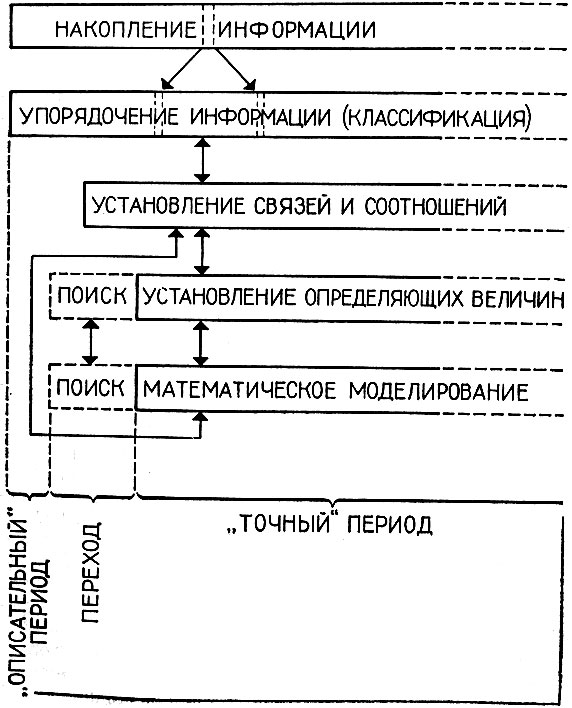
Рис. 1. Схема развития наук

Сейчас, когда наука развивается не трудами отдельных энтузиастов, как было всего каких-либо сто лет назад, а целыми армиями научных работников, темпы накопления информации стали столь велики, что мы приходим уже к информационному кризису, который можно охарактеризовать тем, что количество вновь приобретаемой информации сравнивается с количеством теряемой информации. Дело, конечно, не в том, что она теряется физически. Нет, она содержится физически в научных статьях, в каких-либо отчетах, но человек практически не может ее найти. Реферативные журналы облегчают положение лишь временно, ибо скоро человек будет не в состоянии и их пересматривать.

Положение могут спасти лишь автоматизированные информационные системы, базирующиеся на вычислительной технике. Создание таких систем (в смысле программного обеспечения), разработка языков обращения к системам есть задача современной математики.

Мы уже говорили о том, что не только наивная классификация, но и научная могут быть субъективными. Постараюсь высказаться более определенно. Пусть на меня не обижаются ботаники и зоологи, но системы классификации, существующие в этих науках, все субъективны. Почему? Прежде всего методика классификации совершенно не формализована. Никто не может сказать, что такое отряд, семейство, род, а вводятся теперь и подотряды, и надсемейства, и подсемейства и подроды.

Во-вторых, разделение группы производится по небольшому числу признаков, просто потому, что с большим числом признаков человек не может обращаться. Если, например, мы возьмем десять признаков и каждому признаку будем придавать лишь два значения (признак присутствует - 1, признак отсутствует - 0), то уже мы будем иметь 1024 классификационные группы (2¹⁰). С этим человек за всю свою жизнь, может быть, еще и сможет справиться. Но при двадцати признаках число групп будет уже больше миллиона (2²⁰). С этим никакой гений не совладает. Поэтому и приходится человеку ограничивать себя небольшим числом признаков.

Я отнюдь не хочу упрекать ботаников и зоологов за ту колоссальную работу, которая ими проделана но систематике. Они сделали все, что было в их силах. Но как только мы ограничиваемся малым числом признаков, классификация становится субъективной. Она полностью определяется выбранными признаками, а этот выбор субъективен. И то, что выбор делается на основании многолетнего, даже векового опыта, не исключает субъективности. Опыт позволяет лишь отбросить несущественные признаки.

Для объективности классификации необходимо, чтобы число возможных классификационных групп значительно превосходило число классифицируемых объектов. Если, как мы уже приводили пример, каждый признак принимает два значения и если число объектов N, то должно выполняться условие 2ⁿ >> N, где n - число признаков.

Ну, например, известно, что число видов моллюсков-гастропод составляет порядка 80 000. Значит, для их объективной классификации необходимо использовать (одновременно, а не поочереди) много больше 17 признаков.

Без помощи самой новейшей вычислительной техники такого объема комбинаторный анализ человек произвести не может.

Хотя цель классификации в общем довольно прагматическая - облегчить анализ накопленной информации - однако можно надеятся, что сбъктивная классификация будет отражать генетические связи, выявление которых - одна из главных задач таких наук, как ботаника и зоология.

В решении задач третьего русла - установления связей и соотношений - применение математических методов можно считать традиционным. Статистический, комбинаторный, логический анализ - это те разделы математики, которые позволяют выявлять соотношения между объектами. Речь идет сейчас о том, чтобы наиболее полным образом охватить накопленную информацию и проанализировать ее в различных аспектах. Представляется вероятным, что уже современная вычислительная техника может существенно облегчить эту задачу.

Статистический анализ давно используется почти во всех описательных науках. Менее традиционно применение логического анализа, который может оказаться особенно эффективен в науках социологического цикла.

Наконец, переходим к руслам математического моделирования и установления величин. Очевидно, что математическое моделирование без математических методов решения модельных уравнений невозможно. Но проблема здесь состоит не в решении модельных уравнений, а в их составлении (по крайней мере на современном этапе). Почему же так преуспели физики и так далеки еще от них, скажем, биологи, хотя науки эти примерно одного возраста? Мы уже обращали внимание на исключительную простоту законов Ньютона - математической модели механических движений. Но ведь механическое движение - это простейшая форма движения материи, и у нас нет никаких оснований ожидать, что определяющие соотношения в биологии будут столь же простыми, как в механике или в других разделах физики. Поэтому и процесс построения математических моделей в описательных науках будет значительно более сложным. Оптимизм здесь порождает то обстоятельство, что сейчас мы располагаем несоизмеримо более мощными средствами решения модельных уравнений, их сопоставления с огромным накопленным материалом, чем во времена Ньютона, Кулона, Фарадея и даже Шредингера. Ведь сейчас электронные вычислительные машины за один день производят больше вычислений, чем мог сделать человек за 3000 лет (при технике всего тридцатилетней давности, не говоря уже о временах Аристотеля).

Но один этот факт еще не решает дела. Необходимо изменение всего процесса исследований. Человек должен вести исследования совместно с машиной, или, как говорят сейчас, в режиме постоянного диалога с машиной. Схематически этот процесс можно разбить на шесть этапов:

1. Продуцирование соображений о возможных формах связей (человек);
2. Составление варианта метематической модели (человек);
3. Решение модельных задач (машина);
4. Cравнение результатов решения с накопленной информацией, определение несоответствий (машина);
5. Анализ возможных причин несоответствия (человек);
6. Составление нового варианта модели (человек).

Далее идут повторения цикла от 2 до 6.

При положительном результате после некоторого числа циклов, число которых зависит от здравого смысла человека, модель может быть принята, при отрицательном - необходимо возвращение к пункту 1.

Естественно, исправление вариантов модели (п. 6) может быть интуитивным или расчетным. Во втором случае требуется методика расчета, а расчет выполняется машиной.

Наиболее трудным этапом является установление величин. Мы еще не представляем, как этот этап можно формализовать. Люди обычно называют подобного рода открытия интуицией, или вдохновением, но эти слова мы не можем передать машине. Ясно, однако, что эти определяющие величины находятся в содержании третьего русла, их нужно суметь распознать. Таким образом, возникает особая проблема распознавания образов, значительно более сложная, чем та, с которой мы сталкиваемся, например, на этапе классификации или в процессе идентификации на нашей схеме развития науки.

В заключение мне хотелось бы так резюмировать сказанное выше. Применение математических методов может начинаться в каждой науке с самого начала ее зарождения, а не только с того момента, когда составлены математические модели, достаточно точно описывающие процессы, изучаемые этой наукой. Применение математических методов на этих ранних этапах может существенно ускорить процесс перехода от "описательного" к "точному" этапу развития.