Алгебра

Алгебра как искусство решать уравнения зародилась у вавилонян, у которых было для него специальное название, перешедшее в арабский язык.

Ал-Хорезми свою книгу начала IX века, которая, трижды переведенная в XII веке на латинский язык, стала родоначальником европейских учебников алгебры, называет "Китаб ал-джебр вал-мукабала", что в переводе означает: "Книга о восстановлении и противоставлении". "Восстановление" означает превращение отрицательного числа в положительное при перенесении из одной половины уравнения в другую. Так как в те времена отрицательные числа не считались настоящими числами, то операция ал-джебр (алгебра), как бы возвращающая число из небытия в бытие, казалась чудом этой науки, которую в Европе долго после этого называли "великим искусством".

Термин "алгебра" как название искусства восстановления у арабов же перешел в медицину. Вправление кости ломаной руки или ноги также являлось восстановлением потерянного органа, и искусство врача, которое возвращает человеку руку или ногу, также стали называть алгеброй.

Такой двойной смысл слова "алгебра" объясняет нам один странный на первый взгляд факт. Во второй части известного романа Сервантеса "Дон Кихот" (глава XV) рассказывается, как дон Кихот сбил с лошади своего противника, как тот лежал на земле, не будучи в состоянии шевелить ни руками, ни ногами, и как дон Кихоту удалось найти алгебриста для оказания помощи побежденному противнику.

Так сказано в испанском оригинале романа, так же говорится в более ранних русских изданиях "Дон Кихота", только в последнем издании "алгебрист" заменен "костоправом". Объясняется это тем, что в испанском и португальском языках слово "алгебра", как и в арабском языке, означает не только часть математики, но и "искусство вправлять вывихи": словом "алгебрист" называется не только знающий алгебру, но и врач - специалист по болезням рук и ног.

Арабы в течение нескольких столетий владели частью Пиренейского полуострова и принесли туда начала своей культуры и культуры, заимствованной ими у других народов. В частности, у наших народов Средней Азии. Узбекские и Таджикские ученые обогатили науку, а в ряде случаев утвердили ее славу на все времена.

Арабы принесли сочинения по математике Мухаммеда ал-Хорезми (Мухаммед из Хорезма), Абдуль ал-Фергани и других ученых, а также переводы греческих авторов. Много арабских слов вошло в испанский и португальский языки, в том числе и слова "алгебра" и "алгебрист" в тех двух значениях, которые эти слова имели у арабов.

Говорить об алгебре у египтян нет основания.

Египтяне решали задачи, которые мы теперь решаем при помощи уравнений первой степени, методом ложного положения. Эти же задачи решаются в арифметике, но мы не называем арифметику из-за этого алгеброй.

Греческим геометрам (Евклид) были известны основные алгебраические операции, но они прилагали их только к отрезкам прямой.

Только у позднего греческого математика Диофанта мы находим числовое решение уравнений первой и второй степени в то время, когда греческая математика уже замирает (III или IV век нашего летосчисления). Как теперь известно, индусы примерно в то же время стали разрабатывать алгебру, но Европа ознакомилась с подлинными индусскими математическими работами лишь в девятнадцатом столетии.

Основания алгебры как искусства решать уравнения уже давно до этого через книгу ал-Хорезми дошли до Европы и были европейскими математиками разработаны и развиты дальше.

Буквенная символика алгебры. Уже ал-Хорезми характерную особенность алгебры видел в том, что она решает задачи, которые рассматриваются и в арифметике, в общем виде. В наше время достигается это тем, что числа обозначаются буквами, которые, в зависимости от условий задачи, могут получать разные числовые значения.

Алгебру поэтому часто называли общею или универсальною арифметикою.

Употребление букв в алгебре появилось в результате очень долгого развития.

Начатки употребления особых знаков для обозначения искомых чисел и операций над ними, так называемой буквенной символики в алгебре, можно видеть уже у древних вавилонян.

Особый знак для обозначения неизвестного искомого числа, называвшегося "кучей", был у египтян.

Греческий математик Диофант имеет знаки для обозначения неизвестного и его степеней, действия вычитания и равенства. Он же знает, что можно производить умножение выражений вроде (5-3) (4-2), не находя предварительно разностей, причем произведение чисел, перед которыми стоят одинаковые знаки, надо писать слагаемым, то есть с плюсом, а произведение чисел, перед которыми стоят разные знаки, надо писать вычитаемым, то есть с минусом. Отрицательного числа у Диофанта еще нет.

Индусские математики при решении уравнений смелее применяли те же правила, что и Диофант, и при решении квадратных уравнений стали рассматривать и отрицательные корни, которые они толковали как долг или расход и обозначали точкой над числом или крестиком рядом с ним. Но еще индусский математик XII века заявляет, что "люди таких чисел не одобряют". Равноправность положительных и отрицательных чисел была признана в математике лишь в XVII веке.

Математики, писавшие на арабском языке, в том числе среднеазиатские, неизвестное искомое число называли "вещью" (буквенной символики они не имели). Первая буква этого слова в европейской транскрипции и дала наше обозначение неизвестного буквой х.

До шестнадцатого столетия, однако, изложение алгебры было словесным. Французский математик Виет (1540-1603) и его современники вводят буквенные обозначения и символы в широком масштабе, хотя не сразу в таком виде, как мы делаем это в настоящее время.

Хотя уже в начале XVI века отдельные математики ввели обозначение степени числа при помощи показателя степени, но еще в XVIII веке встречаются записи аа, ааа или аааа вместо а², а³ и а⁴. Даже знак =, столь удобный и понятный, вошел во всеобщее употребление только в XVIII веке, и еще в начале этого века даже авторы научных книг считают нужным объяснять, что знаки + и - обозначают сложение и вычитание, знак x - умножение.

Происхождение употребляемых нами в арифметике и алгебре знаков не всегда можно точно установить.

Полагают, что знаки + и - возникли в торговой практике. Виноторговец черточками отмечал, сколько мер вина он из бочки продал. Приливая в бочку новые запасы, он перечеркивал столько расходных черточек, сколько мер он восстановил. Так, якобы, произошли знаки + и - в XV веке.

Происхождение знака - таким образом кажется правдоподобным.

Относительно происхождения знака + существует другое объяснение, не менее правдоподобное. Вместо a+b писали "а и b", по-латыни "a et b". Так как слово "et" - "и" - приходилось писать очень часто, то его стали сокращать: писали сначала одну букву t, которая в конце концов выродилась в знак +. В книгах по арифметике вместо них долго писали латинские буквы р (плюс) и т (минус).

Знаки x и · для обозначения умножения и знак : для деления входят в употребление только в семнадцатом столетии. До введения этих знаков употребляли для обозначения умножения и деления буквы М и D, как первые буквы латинских названий этих действий.

Про знак √ обычно указывается, что он происходит от буквы r (первой буквы латинского слова "rаdix" - "корень"). Это объяснение не является общепринятым. В самых старых рукописях перед числом, из которого нужно извлечь корень, ставилась точка, а позднее - ромбик с острыми углами вверх и вниз. Для обозначения квадратного корня этот знак стали снабжать одной косой черточкой, отчего получился знак √.

Скобки в современном виде вошли в употребление лишь в XVIII веке и, прежде всего, в широком масштабе в изданиях Петербургской академии наук.

Само название "скобки" было введено нашим академиком восемнадцатого столетия Эйлером (1770). До этого, вместо заключения выражения в скобки, над ним или под ним проводили черту. Если из алгебраического выражения нужно было извлечь корень, то перед ним ставили знак корня - ромбик с косой черточкой и над выражением проводили черту. Так образовался наш знак корня √ (радикал).

Неизвестные числа с XVII века стали обозначать последними буквами латинского алфавита х, у, z. Однако долго еще неизвестное в уравнении писали буквой R (от Radix - корень), а квадрат его - буквой q (quadratus) Рассмотрите снимок части титульного листа "Арифметики" Магницкого. В руке Архимеда доска с такою записью.

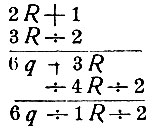
Здесь знак есть старинный знак вычитания. Запись Магницкого в наших обозначениях следующая:

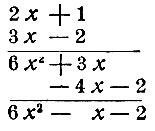
После введения буквенной символики в алгебру и усвоения понятия отрицательного числа, решение уравнений первой степени свелось к законам действий над числами. Никакого "открытия" способа решения этих уравнений не надо было сделать, и такое открытие никем не отмечено.

Часть титульного листа 'Арифметики' Л. Ф. Магницкого

Существующие способы решения систем уравнений первой степени все уже имеются в книге Ньютона "Всеобщая арифметика", которая была издана в 1707 году ив 1948 году вышла в русском переводе.

Первой оригинальной русской книгой по алгебре является: "Начальное основание математики, сочиненное Николаем Муравьевым, капитан-порутчиком от инженеров, часть I, Петербург, 1752". Самым значительным оригинальным русским руководством по алгебре в XIX веке была "Алгебра или вычисление конечных. Сочинил Н. Лобачевский. Казань, 1834". В этой книге наш великий математик Н. И. Лобачевский как в научном, гак и в методических отношениях предвосхитил многое, к чему западноевропейские ученые и педагоги пришли позднее.