Дробное число

Дроби бывают трех видов:

1) доли или единичные дроби, у которых числитель единица, знаменателем же может быть любое целое число;

2) дроби систематические, у которых числителями могут быть любые числа, знаменателями же - только числа некоторого частного вида, например степени десяти или шестидесяти;

3) дроби общего вида, у которых и числители и знаменатели могут быть любыми числами.

Изобретение этих трех различных видов дробей представляло для человечества разные степени трудности, поэтому разные виды дробей появлялись в разные эпохи.

Знакомство человека с дробными числами началось с единичных дробей с малыми знаменателями.

Понятия "половина", "треть", "четверть", "осьмушка" употребляются часто людьми, которые арифметике дробных чисел никогда не обучались. Эти простейшие дроби изобрел каждый народ самостоятельно в ходе своего развития.

Единичные дроби. Древние египтяне, несмотря на то, что они в течение нескольких тысячелетий своей истории развили высокую культуру, оставили после себя прекрасные памятники искусства, владели многими отраслями техники, однако в арифметике дробных чисел не пошли далее изобретения единичных дробей (и дроби 2/3), Если задача приводила к ответу, который мы выражаем дробным числом, египтяне его представляли в виде суммы единичных дробей или долей. Если, например, ответ по-нашему был 7/8,

египтянин представлял его в виде суммы 1/2 + 1/4 + 1/8

и писал без знаков сложения: 1/2 1/4 1/8. Без знака сложения обходились и многие позднейшие народы, понимая писание рядом дробей как сложение. Этот египетский способ письма частично сохранился и у нас. Мы пишем смешанные числа, ставя рядом, без какого-либо соединяющего знака, число целых единиц и дробь, и понимаем запись, как сумму: пишем 3 1/2, вместо 3 + 1/2.

Может показаться, что египетский способ пользования одними лишь единичными дробями делал решение задач сложным. Не всегда это так. Египетский автор решает задачу: нужно разделить 7 хлебов поровну между восемью лицами. Мы сказали бы, что каждый получает 7/8 хлеба.

Для египтянина не было числа 7/8, но он знал, что от деления 7 на 8 получается 1/2 + 1/4 + 1/8. Этот факт подсказывает ему, что для дележа семи хлебов между восемью лицами нужно иметь 8 половинок, 8 четвертей и 8 осьмушек. Он режет 4 хлеба пополам, 2 хлеба - на четвертушки и 1 хлеб - на осьмушки и распределяет доли между получающими. Дли лележа пришлось сделать всего 4+6+7 = 17 разрезов.

Кладовщик, работающий в наши дни, которому предстоит такая же задача деления хлебов, сообразив, что каждому получателю надо дать семь восьмушек, по всей вероятности, разрежет все 7 хлебов предварительно на восьмушки, для чего ему требуется сделать 7x7 = 49 разрезов. Как видим, в этой задаче египетский способ решения является более практичным.

Египетский ученик, решая задачи, приводившие к дробному числу, должен был иметь пред собою таблицу, чтобы знать, в виде суммы каких долей представляется результат деления (дробное число). Такую таблицу мы и находим в начале египетского руководства математики, которое известно нам под названием "папируса Ахмеса" или "папируса Райнда".

Как можно представить любую дробь в виде суммы долей? При нашем знании арифметики это легко сделать.

Можно убедиться (проверьте!) в правильности равенства

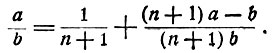
Если n есть целая часть дроби b/a [в математике это обозначают знаком Е (b/a)], или n = Е (b/a), то, пользуясь равенством (*) мы можем дробь a/b представить в виде суммы долей. Покажем это на примере 13/20.

По равенству (*)

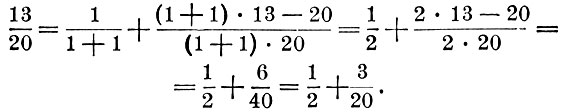
Над дробью 3/20 проделаем те же преобразования:

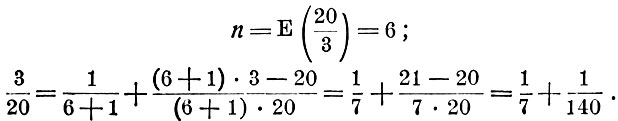
Подставляя это значение вместо 3/20, имеем:

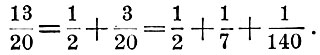
Задача: представьте 17/18 в виде суммы долей.

Ответ: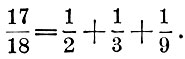

Решение задач практической жизни при помощи одних лишь долей (египетский способ) имело место почти у всех европейских народов, начиная с греков.

Систематические дроби. Одновременно с единичными дробями появились и систематические дроби. Самый ранний по времени вид таких дробей есть шестидесятиричные дроби, употреблявшиеся в древнем Вавилоне. В этих дробях знаменателями служат числа 60, 60² = 3600, 60³ = 216 000 и т. д., и они сходны с нашими десятичными дробями.

Шестидесятиричными дробями все культурные народы пользовались до ХVII века, особенно в научных работах, почему они и назывались физическими или астрономическими дробями, а дроби общего вида, в отличие от них, - обыкновенными или народными. Следы пользования этими дробями остались у нас до сих пор: минута есть 1/60, секунда 1/60² = 1/3600, терция 1/60³ = 1/216000 часть часа.

Десятичные дроби. Десятичные дроби представляют также вид систематических дробей.

Изобретателем их почти во всех книгах называется фламандский (бельгийский) инженер Симон Стевин (1548-1620). Стевин в 1585 году издал брошюру, в которой горячо агитировал за введение в употребление новых, десятичных, дробей, при помощи которых, по его словам, "можно решать все житейские задачи без ломаных" (так назывались дроби у всех народов). Однако, как мы уже знаем, десятичные дроби были введены в научную литературу около 175 лет до него узбекским математиком и астрономом ал-Каши. Вычисляя отношение длины окружности к радиусу в шестидесятиричной системе, в то время общепринятой в научных исследованиях, ал-Каши получает результат в виде записи:

что означает

Под этим числом он пишет:

целых

Это число есть перевод написанного выше значения числа 2π из шестидесятиричной системы счисления в десятичную и представляет десятичную дробь

Разделив это число на 2, получим приближенное значение π - отношение длины окружности к диаметру

В этой дроби все 16 знаков после запятой точны.

Десятичные доли ал-Каши называет: десятичные минуты, десятичные секунды, десятичные терции и т. д.

В написанном в 1427 году "Ключе к искусству "счета" ал Каши дает правила вычислений в десятичной системе, то есть учит умножению и делению десятичных дробей.

Сказанное дает нам полное основание считать узбекского ученого начала пятнадцатого столетия ал-Каши основоположником употребления десятичных дробей и тем ученым, который и обосновал теорию этих дробей.

Кроме этого, в тех же книгах ал-Каши обнаруживает ясное понимание правил

что представляет большой шаг вперед в этом вопросе от употреблявшихся в Западной Европе неуклюжих правил, ведущих свое начало от Архимеда.

Дробь общего вида. Дроби общего вида m/n, в которых и m и n могут быть произвольными целыми числами, появляются уже в некоторых сочинениях

Архимеда. Простейшие из таких дробей: 2/3, 3/4 постепенно входят в употребление в житейской практике. Индусы уже в первые века нашего летосчисления установили современные правила действий над обыкновенными дробями. Эти правила через руководства среднеазиатских математиков - ал-Хорезми и других - вошли в европейские учебники арифметики. Это случилось ранее распространения десятичных дробей.

В "Арифметике" Магницкого (1703) обыкновенные дроби излагаются подробно, десятичные же дроби - в специальной главе, как некоторый новый вид счисления, не имевший при тогдашней системе мер большого практического значения.