Теорема Эйлера - Гольдбаха - Виноградова о простых числах

О простых числах имеется ряд теорем, поражающих своею видимой простотой и трудностью доказательства. Самая известная из них - теорема Гольдбаха, доказательство которой, после двухсотлетних бесплодных усилий очень многих математиков, в наше время почти закончено академиком Иваном Матвеевичем Виноградовым.

В члены основанной в 1725 году Петербургской Академии наук в 1727 году вступил двадцатилетний Леонард Эйлер, оказавшийся одним из самых крупных математиков XVIII века.

Его ими носят десятки теорем и формул во всех разделах математики и механики. Собрание его сочинений охватывает 80 громадных томов. В отличие от ряда академиков-иностранцев XVIII века, Эйлер заслужил уважение и любовь первых русских академиков, в том числе М. В. Ломоносова.

В переписке Эйлера со своим товарищем по Академии Гольдбахом Эйлер в 1742 году на вопрос Гольдбаха отвечает, что он считает истинной следующую теорему, которую, однако, не может доказать: "Всякое четное число, начиная с шести, есть сумма двух нечетных простых чисел":

Если эта теорема верна, то из нее следует, что всякое нечетное число есть сумма трех простых чисел. Эти предложения получили название теоремы Гольдбаха. Относительно четных чисел ее проверяли многие математики. В 1940 году проверка была доведена до 100 000.

Проверку правильности теоремы Эйлера - Гольдбаха - Виноградова для четных чисел можно провести следующим образом. Возьмите две полоски из плотной бумаги и нанесите на них равные клетки. В клетки одной полоски вписывайте нечетные числа в убывающем порядке, начиная с некоторою числа, например, с пятидесяти. На другую полоску напишите нечетные числа в возрастающем порядке, начиная с единицы. Подчеркните на обеих полосках все простые числа по "решету Эратосфена" или таблице простых чисел.

Прикрепите полоски рядом так, чтобы число 49 одной полоски стояло на одной высоте с 1 другой полоски. В таком случае, стоящие рядом подчеркнутые числа на обеих полосках дают представление числа 50 в виде суммы двух нечетных простых чисел. Таких "разбиений" числа 50 оказывается 4, именно: 3 + 47, 7 + 43, 13 + 37, 19 + 31.

Этими же полосками можно воспользоваться для "разбиений" любого четного числа, не превышающего 50, на сумму двух простых чисел. Для этого нужно вторую полоску поместить рядом с первой так, чтобы сумма рядом стоящих чисел оказалась равной разбиваемому числу. На нашей табличке показано "разбиение" чисел 50, 48 и 40. Простые числа напечатаны жирным шрифтом (см. рисунок Проверка теоремы Гольдбаха для чисел; 50, 48 и 40.).

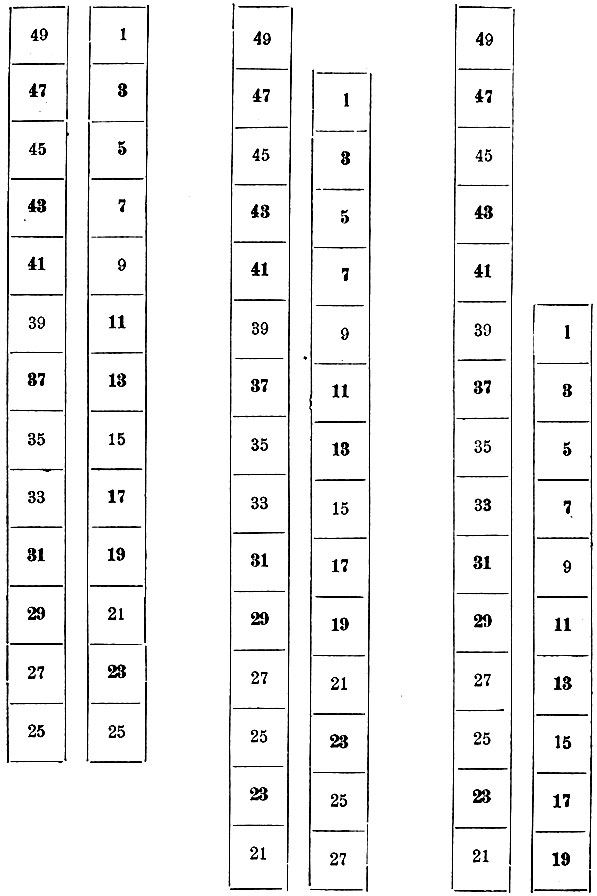
Проверка теоремы Гольдбаха для чисел; 50, 48 и 40

Делалось очень большое число попыток доказать теорему Гольдбаха, но все они остались безрезультатными.

Еще в 1922 году крупнейший английский математик Харди вынужден был заявить, что для доказательства этой теоремы существующая ныне математика недостаточна. Как всегда в таких случаях, для решения вопроса нужно было создать новые методы в математике.

Советский математик Шнирельман Л.Г. (1905-1938)

Начало создания этих новых методов математики было положено в 1930 году советским математиком Л. Г. Шнирельманом (1905-1938); выработаны же необходимые новые методы были академиком Иваном Матвеевичем Виноградовым (родился в 1891 году).

В 1937 году И. М. Виноградов доказал, что всякое достаточно

большое нечетное число есть сумма трех нечетных простых чисел. К. Г. Бороздкин в 1939 году показал, что "достаточно большое число" И, М. Виноградова

где e = 2,71828 . .. Таким образом доказано, что, начиная с этого числа, теорема Гольдбаха для нечетных чисел верна.

Имеет ли теорема Гольдбаха какое-нибудь практическое значение?

Пока не имеет. Однако это нисколько не уменьшает значения достижений И. М. Виноградова и других советских математиков в этом вопросе.

Академик Виноградов И.М. (родился в 1891 году)

Для доказательства теоремы Гольдбаха созданы новые математические методы; и эти методы, раз они найдены, будут использованы для решения других вопросов, которые, наверное, будут иметь практические применения. В развитии любого раздела математики самым важным является изобретение новых методов; применение же этих методов представляет работу несравненно более легкую.

Открытие И. М. Виноградовым его метода доказательства было событием, которое привлекло внимание всего мира.