Чебышев П.Л.

Пафнутий Львович Чебышев родился 2б май 1821 года, умер 8 декабря 1894 года. Воспитанник Московского и профессор Петербургского университетов, член Петербурской и Парижской академий наук, Чебышев сделал много важнейших открытий во многих областях математики и создал целые новые разделы ее. К самым выдающимся достижениям относятся и его работы о простых числах

В 1850 голу П. Л. Чебышев вывел формулу, которую безрезультатно искали самые выдающиеся математики, для определения с большой точностью количества простых чисел, заключенных между 1 и любым числом х. Так как в настоящее время имеется таблица простых чисел, заключающихся между 1 и 10 000 000, то легко проверить степень точности формулы Чебышева в этих границах.

Обозначив, как это принято в математике, действительное количество простых чисел между 1 и числом х символом π (х) (читается, пи от х), а количество их, вычисленное по формуле Чебышева, символом Li (х) (ли от х), находим разницу между ними, то есть Li (х) - π (х) для различных значений х. Эти разности показывай т, на сколько результат, вычисленный по формуле Чебышева, отклоняется от истинного значения искомого числа простых чисел.

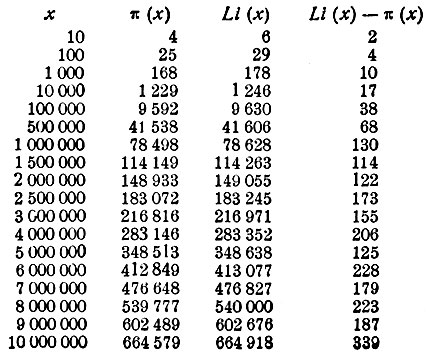
Таблица показывает, что числа, получаемые по формуле Чебышева, в пределах 10 000 000 всегда несколько больше действительных количеств простых чисел, но это отклонение составляет для 500 000 лишь около 0,16%, а для 10 000 000 только 0,05%. Точность формулы Чебышева весьма большая и увеличивается с возрастанием числа х.

Чебышев П.Л. в бытность профессором Петербургского университета

Отметим, что в настоящее время доказано следующее неожиданное свойство чисел Чебышева. В натуральном ряду, очень далеко за пределами 10 000 000, существует число, около которого Li (х) сказывается уже не больше, а меньше числа π (х). В 1933 голу было установлено, что это имеет место для числа х, которое определяется приближенным равенством

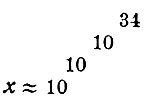
Эю число (так называемое число Скьюза) является самым большим числом, когда-либо встречавшимся в науке. Это число, в котором за единицей следует

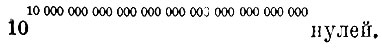
О впечатлении, которое произвело открытие Чебы-шевым формулы для определения числа простых чисел, можно судить по отзывам крупнейших математиков.

Знаменитый английский математик Сильвестер (1814-1897) назвал Чебышева "победителем простых чисел, который первый стеснил их капризный поток в алгебраические границы", и добавил, что "дальнейших успехов в теории простых чисел можно ожидать только тогда, когда родится некто, настолько превосходящий Чебышева своею проницательностью и вдумчивостью, насколько Чебышев превосходил этими качествами обыкновенных людей".

Золотарев Е.И. (1847-1878)

П. Л. Чебышев одновременно разрешил и другую, остававшуюся нерешенной до этого, задачу.

Французский математик Бертран (1822-1900) проверил на всех числах до 6000000 существование следующей закономерности: для всех чисел х, начиная с 4, между числами х и 2 х-2 содержится, по крайней мере, одно простое число. Это предложение было известно под названием "допущения (постулата) Бертрана"4. П. Л. Чебышев доказал предложение Бертрана и превратил его в теорему.

Ляпунов А.М. (1857-1918)

По всему сказанному о П. Л. Чебышеве можно подумать, что это был теоретик, занимавшийся самыми отвлеченными областями математики, далекий от всякой практики.

Марков А.А. (1856-1922)

Между тем он является ученым, который чаще, чем кто-либо из математиков, решал задачи, вытекавшие из практических нужд человека.

Об этом можно судить уже по заглавиям его трудов, среди которых встречаем такие: "Об одном механизме", "О зубчатых колесах", "О простейших сочленениях", "О кройке платьев" и так далее. Он изучал устройство ветряных мельниц, разных заводских установок и, по его словам, повсюду наталкивался на вопросы математики, о которых наука его времени знала мало.

Вороной Г.Ф. (1868-1908)

Эти пробелы в науке П. Л. Чебышев и восполнил своими гениальными теоретическими трудами.

Параллельно с этим он всю жизнь занимался практической механикой, изобрел большое число механизмов, производил опыты по стрельбе и много содействовал достижению русской артиллерией того высокого совершенства, которым она всегда славилась перед артиллериями всех европейских государств.

Вся деятельность Чебышева представляет постоянное сочетание теории и практики; руководила этою деятельностью одна и та же идея, которая, по мнению Чебышева, лежит в основе всякой человеческой деятельности: как при наименьшей затрате сил получить наилучшие результаты, кик располагать своими средствами для достижения по возможности большей выгоды. Прилагая эту идею к улучшению средств вычисления, он дал формулы, применение которых одним из его талантливых последователей, академиком А. Н. Крыловым, позволило в такой мере улучшить расчеты кораблестроения, что Россия и в этом отношении уже много десятилетий стоит выше остальных стран мира.

Наконец нужно отметить, что П. Л. Чебышев создал первую русскую математическую научную школу, отличительной чертой которой является решение, возможно простыми средствами, конкретных вопросов, с доведением решения до формулы, по которой можно получить числовой результат.

К этой школе принадлежат почти все славные имена русских математиков второй половины XIX и начала XX века: A. H. Коркин, Е. И. Золотарев, А. М. Ляпунов, А. А. Марков, Г. Ф. Вороной, В. А. Стек-лов, A. H. Крылов и многие другие.