
Арифметика целых чисел
Употребляемые в настоящее время способы производства арифметических действий над целыми числами выработались постепенно в Индии в связи с распространением там ранее других стран поместной десятичной нумерации. Самое раннее письменное свидетельство о существовании этой индусской арифметики относится к середине седьмого столетия. Около 660 года сирийский ученый Север Себокт пишет: "Высокие открытия индусов в астрономии более гениальны, чем открытия греков и вавилонян; их ценные методы вычисления превосходят всякое описание. Скажу лишь, что вычисления делаются при помощи девяти цифр ..."Первые следы проникновения этих приемов в Европу можно констатировать в редких памятниках конца X века.

Первая наша газета 'Ведомости' еще в 1703 году употребляет славянские цифры: 'На Москве вновь ныне пушек медных, гаубиц и мортиров вылито 400. Те пушки ядром по 24, по 18, по 12 фунтов' и так далее
Более широкое знакомство с ними в Европе началось с XIII века, после того как в XII веке на латинский язык была переведена книга узбекского математика Мухаммеда ал-Хорезми - "Арифметика индусскими цифрами".
Индусские правила действий над целыми числами отличались от наших лишь тем, что все действия начинались слева, с высших разрядов.
Индусы писали на дощечках, усыпанных порошком, поэтому им легко было "стереть" написанную цифру и заменить новою, если действие над следующим разрядом давало результат, часть которого надо было прибавить к высшему разряду,

Академик А. Н. Крылов (1863-1945)
При нашем способе письма на бумаге это стирание неудобно. Однако профессиональные вычислители и в наше время производят действия, начиная с высших разрядов. Так, например, при сложении нескольких чисел они складывают два числа, начиная с высших разрядов, и пишут полученную сумму рядом. Затем эту сумму таким же образом складывают с третьим слагаемым, новую сумму - с четвертым и так далее.
Академик А. Н. Крылов (1863-1945), крупнейший математик нашего времени и, несомненно, лучший вычислитель среди математиков, усердно рекомендовал такой способ производства арифметических действий. Если так поступают профессиональные вычислители, то, очевидно, такой порядок вычисления является более экономным в смысле избежания ошибок, чем принятый в школьном преподавании.
Л. Ф. Магницкий в главе об умножении указывает, что "нецыи умножают странным некоим образом", располагая действия так:

"Странность" этого способа умножения заключается только в том, что умножение начинается с умножения на высший разряд множителя.
Так поступать естественно уже потому, что важнейшая часть произведения получается от умножения на высший разряд множителя. При умножении приближенных чисел этот способ несравненно более удобен, чем обычный.
Вообще арифметические действия в разные эпохи выполнялись различными способами.
Остановимся здесь только на одном способе умножения, о котором в последнее время не раз писали в зарубежных изданиях под названием: "Способ умножения русских крестьян". Он заключается в следующем.
Пусть требуется выполнить умножение 47x33. Составляем два столбца чисел, начиная с данных чисел, один - умножением на два, другой - делением на два. Имеем:

Произведение 47x33 получается от сложения тех чисел первого столбца, которые стоят против нечетных чисел второго столбца, в данном случае 47x33 = = 1504 + 47 = 1551.
Для обоснования такого способа умножения произведем сначала по этому способу вычисление произведения 47x32:
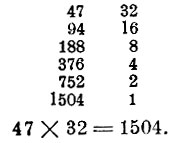
Очевидно, что произведение любой пары соответственных чисел обоих столбцов в этом примере одно и то же, так как, идя сверху вниз, мы один сомножитель увеличиваем, другой уменьшаем в два раза, от чего произведение не изменяется. Следовательно, 47x32= 1504x1 = 1504.
Такая картина будет во всех тех случаях, когда множитель является степенью числа 2. Если же множитель не представляет собою степени числа 2, то, кроме последнего числа второго столбца, которое всегда равно единице, во втором столбце встречается еще хоть одно нечетное число (в первом нашем примере 33). Соответствующее этому нечетному числу число первого столбца (47) надо взять в качестве слагаемого при вычислении произведения, так как, переходя от первой пары чисел ко второй, мы отбросили от произведения один раз 47; при умножении 47 на 32 мы имели бы во второй строке те же числа: 94 и 16. Такое отбрасывание из произведения числа, стоящего в первом столбце, происходит каждый раз, когда мы во втором столбце имеем нечетное число.
Найдем произведение: 53x49.
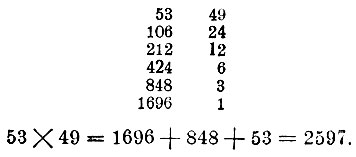
53x49 = 1696 + 848 + 53 = 2597
Этот способ умножения является практичным, если приходится одно и то же число умножать на разные числа. Пусть, например, счетовод колхоза, не имеющий арифмометра, вычисляет причитающиеся разным лицам суммы, при условии, что каждый рабочий данного разряда получает в день 53 рубля.
Первый столбец, получаемый последовательным удвоением, является общим при всех умножениях и вычисляется раз навсегда. Для получения сумм, причитающихся за различные числа трудодней, остается составлять лишь для каждого числа дней второй столбец чисел делением на два, что легко выполняется в уме.
"Способ умножения русских крестьян" заключается в замене умножения сложением и простейшими случаями умножения и деления чисел на 2. Умножение и деление произвольных чисел представляли для человека большие трудности. Сначала были усвоены действия умножения и деления на 2, которые под названием "удвоения" и "раздвоения" чисел в течение многих столетий в учебниках арифметики рассматривались, как особые арифметические действия. "Способ умножения русских крестьян" представляет удобный прием для замены более сложного арифметического действия - умножения произвольных чисел - действиями более простыми: сложением, "удвоением" и "раздвоением".
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'