
Задача Менделеева Д.И.
Наш знаменитый химик Д. И. Менделеев, будучи директором Главной палаты мер и весов, интересовался задачей, если имеем набор гирь, по одной каждого вида, например, в а, b, с и d граммов, - то по сколько граммов должны быть эти гири, чтобы при помощи их можно было взвесить любой груз, не превышающий а + b +с + d граммов?
Задачу эту решали уже много столетий назад, причем решение занимало целые книжки, которые имеются и на русском языке. Однако она решается легко при помощи систем счисления с основанием 2 и 3.
Число в десятичной системе счисления, например, 7438, можно написать так:
7438 = 7 · 1000 + 4 · 100 + 3 · 10 + 8 · 1
или
7438 = 7 · 103 + 4 · 102 + 3 · 10 + 8 · 1.
Запись числа в системе с другим каким-нибудь основанием г имеет вид:
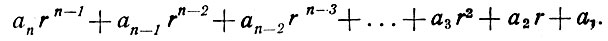
Здесь а1 есть цифра единиц; а2 - цифра единиц второго разряда; а3 - цифра единиц третьего разряда, и т. д.
Числа в системах с основанием 2 или 3 (в двоичной или троичной системе) пишутся в виде:
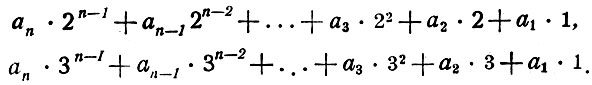
Количество единиц любого разряда в числе, написанном по десятичной системе, не может быть больше 9; в числе, написанном по троичной системе, в каждом разряде может быть единиц только 0 или 1 или 2, а в двоичной системе - только 0 или 1.
Вообще в системе счисления с основанием r в каждом разряде может быть единиц не более r-1. Так в данной выше записи числа с основанием r буквы а1, а2, а3..., аn-1, аn обозначают числа, не превосходящие r-1 то есть, а1 < r, а2 < r,... аn-1 < r, аn < r.
Всякое число десятичной системы можно написать в системе с любым иным основанием, например в двоичной или троичной. Пусть, например, требуется число 743 написать в двоичной системе.
Разделим данное число на 2. Остаток покажет, сколько единиц первого разряда будет в искомом выражении данного числа в двоичной системе. Если частное от деления больше единицы, то его, в свою очередь, надо делить на 2; второй остаток даст число единиц второго разряда искомого числа, а частное вновь надо делить на 2 до тех пор, пока оно не будет меньше 2, после чего следующее частное уже будет равно 0.
Это обращение числа десятичной системы в двоичную удобно расположить следующим образом, делая деление в уме и составляя таблицу с правой руки.

В данном примере IX частное равно 1, деление его на два дает целое частное 0 и остаток 1. Получаемые остатки суть цифры искомого числа в двоичной системе, идущие в том же порядке, как и остатки при делении. Таким образом имеем
74310 = 10111001112.
Индексы 10 и 2 при этих числах обозначают, что число 743 десятичной системы, число 1011100111 - двоичной.
Таким же образом обратим 743 в троичную систему:
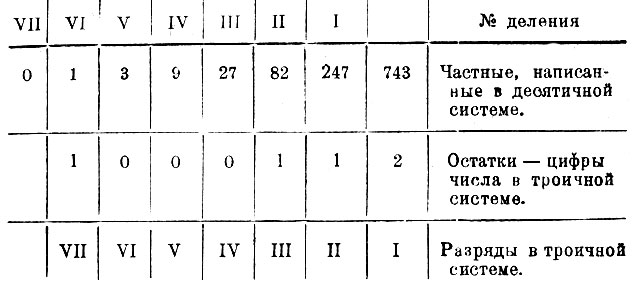
Последнее деление 1:3 дает в частном 0, остаток 1.
Число 743 в троичной системе, таким образом, напишется:
74310 = 10001123
Вернемся к задаче о гирях. Пусть имеем груз в 93 грамма. Какие нужно взять гири, чтобы, имея только один набор их, уравновесить этот груз, кладя гири только на правую чашку весов?
Так как всякое число можно выразить в двоичной системе, и в этом выражении в каждом разряде может быть не более одной единицы, то очевидно, что всякий груз, содержащий целое число граммов, можно уравновесить гирями "двоичной системы" (1, 2, 4, 8, 16...), имея только один набор таких гирь и кладя их только на одну чашку весов.
Выразим число 93 в двоичной системе:
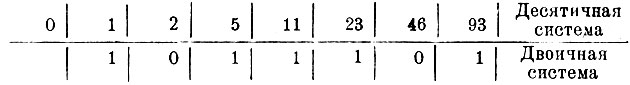
9310 = 10111012 = 1 · 26 + 0 · 25 + 1 · 24 + 1 · 23 + 1 · 22 + 0 · 2 + 1 = 1 · 64 + 0 · 32 + 1 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 1.
Отсюда видно, что при взвешивании груза в 93 грамма на правую чашку весов надо класть гири весом ь
1 + 4 + 8 + 16 + 64 = 93 грамма.
Вообще, имея гири "двоичной системы", то есть
1, 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, 26 = 64 ...
имеем возможность составить вес любого груза, не превышающего сумму весов гирь:
1 + 2 + 4 + 8 + 16 + 32 + 64 + ...
Для этого нужно число граммов (вес) выразить в двоичной системе, что всегда возможно; цифры полученного числа показывают, какие гири нужно класть на правую чашку весов.
Если иметь один набор гирь иного веса, скажем, в 1, 6, 10, 20, 50, 100 граммов, то может оказаться, что не всякий груз, не превышающий суммы весов имеющихся гирь (в нашем примере 186 граммов), может быть уравновешен этими гирями. Так, например, из этих гирь не составить 47 граммов.
Если при взвешивании груза класть гири и на левую чашку весов, то является самым удобным набор гирь в троичной системе в
1, 3, 32 = 9, 33 = 27, 34 = 81 (и так далее) граммов.
Имея 5 таких гирь, можно взвесить любой груз, не превышающий
1 + 3 + 9 + 27 + 81 = 121 грамм.
Пусть имеем груз в 112 граммов.
Выразим число 112 в троичной системе:

11210 - 110113 = 1 · 34 + 1 · 33 + 0 · 32 + 1 · 3 + 1 · 1.
В этом случае достаточно класть на правую чашку гири
1 + 3 + 27 + 81 = 112 граммов.
Чтобы взвесить груз в 64 грамма, выразим число 64 троичной системе:

6410 = 21013 = 2 · 33 + 1 · 33 + 0 · 3 + 1 · 1.
Для взвешивания груза на правую чашку нужно было бы положить 2 гири по 27 граммов, 1 гирю в 9 граммов и 1 гирю в 1 грамм. Как быть, если мы имеем только один набор гирь?
Для этого сообразим, что число 21013 можно выразить только единицами, если, кроме сложения единиц, разрешить также и их вычитание. В самом деле, 2 = 3 - 1 для любого разряда, а 3 - это уже единица высшего разряда; поэтому в троичной системе 2 = 103 - 1. Наше число 6410 = 21013 можно написать как разность: 21013 = 101013 - 10003 только единицами.
Но вычитание веса при взвешивании осуществляется, если гири будем класть на противоположную чашку. Поэтому, чтобы вывесить 64 грамма одним набором гирь троичного счисления, надо на одну чашку положить гири 81 грамм +9 граммов +1 грамм, то есть 91 грамм, а на другую чашку положить 27 граммов. Получим вес 91 - 27 = 64 грамма, что и требовалось.
Итак, посредством выражения веса в троичной системе в виде разности чисел, не содержащих знаков, кроме 0 и 1, мы можем любой вес однозначно разложить на сумму и разность степеней числа 3, то есть найти те гири, которыми выразим данный вес.
Приведем два примера:
1) Составить 113 граммов из гирь троичной системы.
Выразим число 113 в троичной системе
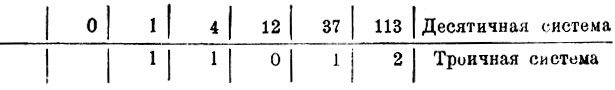
11310 = 110123. Но 110123 = 110123 + 1 - 1 = 110203 - 1 = 110203 - 1 + 103 - 103 = 111003 - 103 - 1.
Значит, на одну чашку надо положить 9 + 27 + 81, а на другую -3 и 1 грамм. Получим 117 - 4 = 113 граммов.
2) Составим 131 грамм из гирь троичной системы.

13110 = 112123 = 112123 + 1 - 1 = 112203 - 1 = 112203 - 1 + 103 - 103 = 120003 - 1 - 103 = 200003 - 1 - 103 - 10003 = 1000003 - 1 - 103 - 10003 - 100003.
Иначе говоря, 131 = 243 - 1 - 3 - 27 - 81.
Естественно возникает вопрос, была ли когда-нибудь на практике осуществлена такая система гирь? По-видимому, это имело место только один раз и именно у нас, в России.
Наш закон о мерах и весах 1797 года, который действовал до 1842 года, установил обязательный набор гирь в 1 и 2 пуда, 1, 3, 9, 27 фунтов и 1, 3, 9, 27 и 81 золотник.
Была издана официальная "Таблица для развеса гирь", дающая все веса до 40 фунтов (1-го пуда) в гирях по троичной системе, иными словами, - готовые результаты перевода всех чисел до 40 в троичную систему счисления. Это мероприятие свидетельствует о том, что еще в ту отдаленную эпоху у нас жизнь строили на научной основе.
Показателем передового характера метрологической мысли в России служит факт, что в комиссии мер и весов в восемнадцатом столетии работали знаменитый наш академик Л. Эйлер и его ученики, из которых известны, как деятели математического образования академики С. Я. Румовский, 0. К. Котельников, М. Е. Головин (племянник М. В. Ломоносова) и другие.
В торговой практике эта система гирь не нужна, так как употребляемые в магазинах гири дешевы и их всегда можно иметь несколько наборов. Но в лабораториях, в которых производятся взвешивания изготовляемыми из дорогих металлов (например, платина намного дороже золота) точными гирями, является весьма существенной возможность обходиться наименьшим числом гирь. Изготовление таких гирь - дело очень сложное, и такие гири стоят очень дорого не только из-за ценности их материала.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'