Из содержания старинных русских руководств по математике

Старинные русские руководства по математике, рукописные и печатные, содержат много такого, что полезно знать изучающему математику и в наше время. Остановимся на трех вопросах: на правиле ложного положения, на занимательных задачах и на математических забавах.

"Фальшивое правило". Так называют старые русские руководства способ решения задач, который теперь известен под названием "правила ложного положения".

При помощи этого правила в старинных руководствах решаются задачи, приводящие к уравнениям первой степени.

Глава "Уравнения первой степени" в этих руководствах отсутствует. Современные способы решения уравнений первой степени предполагают знакомство с понятием отрицательного числа, которое распространялось медленно.

Математик мировой величины, петербургский академик Л. Эйлер, еще в конце XVIII века высказывает об отрицательных числах мнения, которые для нас неприемлемы.

Знакомство с тем, как при отсутствии знаний об отрицательных числах приходилось простые задачи решать искусственным "фальшивым правилом", показывает нам, что скучноватые упражнения над отрицательными числами, которыми мы занимаемся в первых разделах курса алгебры, позволяют в дальнейшем решать задачи на уравнения первой степени гораздо проще, чем это делали еще наши прапрадеды.

Академик Л. Эйлер, в разные годы жизни

Вот решение задачи способом ложного положения или фальшивым правилом у Магницкого.

Памятник академику Эйлеру на Ленинградском Смоленском лютеранском кладбище. Надпись: 'Леонарду Эйлеру Петербургская Академия 1837'

"Спросил некто учителя: сколько у тебя в классе учеников, так как хочу отдать к тебе в учение своего сына. Учитель ответил: если придет еще учеников столько же, сколько имею, и полстолько и четвертая часть и твой сын, тогда будет у меня учеников 100. Спрашивается, сколько было у учителя учеников?" Магницкий дает такой способ решения.

Делаем первое предположение: учеников было 24.

Тогда по смыслу задачи к этому числу надо прибавить "столько, полстолько, четверть столько и 1"; имели бы:

то есть на 100 - 67 = 33 меньше (чем требовалось по условию задачи); число 33 называем "первым отклонением".

Делаем второе предположение: учеников было 32.

Тогда имели бы:

то есть на 100 - 89 = 11 меньше (второе отклонение).

На случай, если при обоих предположениях получилось меньше, дается правило: помножить первое предположение на второе отклонение, а второе предположение на первое отклонение, отнять от большего произведения меньшее и разность разделить на разность отклонений:

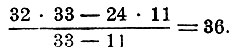
Учеников было 36.

Таким же правилом надо руководствоваться, если при обоих предположениях получилось больше, чем полагается по условию. Например:

Первое предположение: 52.

Получили на 144 - 100 = 44 больше (первое отклонение).

Второе предположение: 40.

Получили на 111 - 100 = 11 больше (второе отклонение).

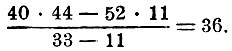
Если при одном предположении получим больше, а при другом меньше, чем требуется по условию задачи, то нужно при указанных выше вычислениях брать не разности, а суммы. Например:

Первое предположение: 60.

Получили на 166 - 100 = 66 больше (первое отклонение).

Второе предположение: 20.

Получили на 100 - 56 = 44 меньше (второе отклонение).

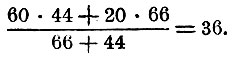
При помощи самых начальных сведений алгебры эти правила легко обосновываются.

Надо решить уравнение ах + b = с. (*)

Первое предположение: х = x₁; ax₁ + b = c₁. (1)

Второе предположение: х = х₂; ax₂ + b = с₂. (2)

Вычитаем равенства (1) и (2) почленно из уравнения (*):

а(х - x₁) - с - с₁ = l₁ (первое отклонение);

а(х - х₂) = с - с₂ = l₂ (второе отклонение).

Разделив почленно два последних равенства, получаем:

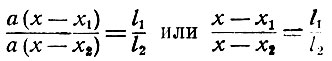
По правилам алгебры делаем следующие преобразования:

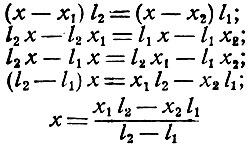
Если отклонения l₁ и l₂ оба отрицательные числа, l₁ < 0 и l₂ < 0, то в правой половине равенства (3) у числителя и знаменателя первые члены будут числами отрицательными, вторые члены - положительными; правило нахождения значения числа х остается то же, что и в первом случае.

Равенство (3) выражает правило ложного положения для тех случаев, когда оба отклонения положительные или оба отрицательные.

Если же l₂ положительно, a l₁ отрицательно (или наоборот), то равенство (3) превратится в

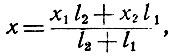
и мы имеем правило ложного положения для случаев, когда отклонения имеют разные знаки.

Средневековые математики дали удобный механический способ применения этого правила под названием "способа весов". Вот как они советуют поступать.

"Рисуй весы. Над точкой опоры пиши число, которое по условию задачи получается после действий над искомым числом. На чашки весов пиши оба предположения. Отклонения "больше" пиши под весами, отклонения "меньше" - над весами. Произведи умножение накрест предположений и отклонений. Если отклонения записаны оба по одну сторону от весов, то надо брать разности; если же отклонения записаны по разные стороны от весов, то надо брать суммы".

Запись наших решений по этому способу следующая:

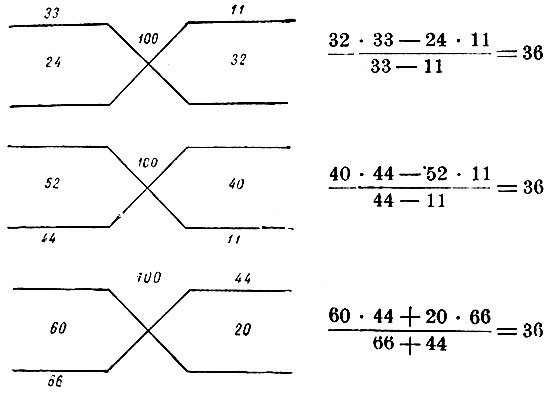
Занимательные задачи встречаются в большинстве русских математических рукописей и печатных руководств старого времени. "Так, например, в них мы встречаем задачу, имеющуюся уже в египетском папирусе Ахмеса в виде задачи о семи кошках, поедающих семь мышей, и т. д.

Соответственная русская народная задача читается так:

Шли семь старцев.

У каждого старца по семи костылей;

на каждом костыле по семи сучков;

на каждом сучке по семи кошелей;

в каждом кошеле по семи пирогов;

в каждом пироге по семи воробьев.

Сколько всех?

Ответ: 137256.

Известен сборник занимательных задач VIII века под названием "Предложения для изощрения ума

Запись наших решений по этому способу следующая: юношества". Эту же цель "изощрения ума" преследует и Магницкий своими задачами.

Вот несколько примеров занимательных задач из ранних русских источников.

Из рукописи XVII века: "Лев съел овцу одним часом, а волк съел овцу в два часа, а пес съел овцу в три часа. Ино хочешь ведати все три - лев, волк и пес - овцу съели вместе вдруг, и сколько бы они скоро ту овцу съели, сочти ми?"

Автор рукописи предлагает следующий прием решения: за 12 часов лев съедает 12 овец, волк -6, а пес -4. Всего же они съедят за 12 часов 22 овцы; следовательно, в час они съедят 22/12 = 11/6 овцы, а одну овцу все вместе - в 6/11 часа.

Из "Арифметики" Магницкого: "Един человек выпьет кадь пития в 14 дней, а со женою выпьет тое же кадь в 10 дней, и ведательно есть, в колико дней жена его особно выпьет тое же кадь".

Ответ: 35 дней.

"Некий человек нанял работника на год, обещав ему дати 12 рублев и кафтан. Но той, работав 7 месяцев, восхотел уйти и просил достойной платы с кафтаном. Он же [хозяин] дал ему по достоинству расчет 5 рублев и кафтан, и ведательно есть, коликие цены оный кафтан был".

Ответ: 48 гривенников.

"Некий человек продае коня за 156 рублев; раскаявся же, купец нача отдавати продавцу, глаголя: "Яко несть мне лепо взяти сицевого коня, недостойного такие высокие ценыа.

Продавец предложи ину куплю, глаголя: "Аще те мнится велика цена сему коню быти, убо купи гвоздие, их же сей конь имать в подковах своих ног, коня же возьми за тою куплею в дар себе. А гвозди во всякой подкове по шести и за един гвоздь даждь ми полушку^*, за другой же две полушки, а за третий копейку, и тако все гвозди купи4*. Купец лее, видя столь малую цену и коня хотя в дар себе взяти, обещал таку цену платити, чая не больше 10 рублев за гвоздие дати. И ведательно есть, колико купец-он проторговался?"

^*(Полушка - 1/4 копейки.)

Ответ: 4178703 3/4 коп.

Задача эта содержится в рукописях XVII века. Она аналогична задаче об изобретателе игры в шахматы, который согласился на скромное вознаграждение - именно, чтобы ему на первую клетку шахматной доски положили одно зерно, на вторую - два зерна, на третью - четыре зерна и так далее, удваивая число зерен каждый раз.

Оказывается, для выполнения этого условия потребовался бы обильный урожай с поля, превосходящего величиною всю сушу земного шара в 28 раз.

В знаменитой "Божественной комедии" Данте (1265-1321) читаем:

 "Заискрилась всех тех кругов краса, 
 И был пожар в тех искрах необъятный; 
 Число же иекр обильней в сотни раз, 
 Чем клеток счет двойной в доске шахматной".

"Счет двойной" означает нарастание чисел при помощи удвоения предыдущего числа, то есть мы имеем тут упоминание о той же старой задаче.

Она, как оказывается, рстречаетея и в наше время не только в сборниках занимательных задач. По сообщению одной газеты 1914 года, у судьи в городе Новочеркасске разбиралось дело о продаже стада в 20 овец по условию уплатить за первую овцу 1 копейку, за вторую - 2 копейки, за третью - 4 копейки и т. д. Очевидно, покупатель соблазнился надеждою дешево купить стадо - и просчитался. Подсчитайте, какую сумму он должен был уплатить. Оказывается, Магницкий не без основания снабдил решение этой задачи предупреждением:

 "Хотяй туне притяжати,
 От кого что приимати,
 Да зрит то себе опасно".

Из "Курса чистой математики" 1786 года Ефима Войтяховского^*:

^*(Войтяховский Ефим Дмитриевич (умер около 1812 года) - штык-юнкер и благородного юношества партикулярный учитель - издал большой "Курс математики" в четырех томах.)

"На вопрос: который час? - ответствовано: 2/5 прошедших часов от полунбчи до сего времени равны 2/3 остальных до полудни. Спрашивается число часов того времени".

Ответ: 7 часов 30 минут.

"У приезжего гасконца оценили богатство: модный жилет с поношенным фраком в три алтына [алтын - 3 копейки] без полушки; но фрак в полтретья [2 1/2 раза] дороже жилета. Спрашивается каждой вещи цена. Ответ: 6 1/4 и 2 1/2.

 "Нововыезжей в Россию французской мадаме
 Вздумалось ценить свое богатство в чемодане:
 Новой выдумки нарядное фуро [платье]
 И праздничный чепец а ла фигаро.
 Оценщик был русак, сказал мадаме так:
 Богатства твоего первая вещь фуро
 Вполчетверта [31/2 раза] дороже чепца фигаро;
 Вообщем стоят не с половиною четыре алтына,
 Но настоящая им цена только сего половина.
 Спрашивается каждой вещи цена,
 С чем француженка к россам привезена".
 Ответ: 5 1/4 и 1 1/2.

Математические забавы в "Арифметике" Магницкого. Забавы в "Арифметике" Магницкого составляют особый раздел "О утешных некиих действах, чрез арифметику употребляемых", начинающийся с указания, что, следуя примеру арифметиков, автор помещает его в свою книгу для утехи и особенно для изошт>ения ума учащихся, хотя эти забавы, по его мнению, "и не зело нужные".

Первая забава. Один из находящихся в компании восьми человек берет кольцо и надевает на один из пальцев на определенный сустав. Требуется угадать, у кого, на каком пальце и на каком суставе находится кольцо.

Пусть кольцо находится у четвертого человека на втором суставе пятого пальца (надо условиться, что суставы считаются, например, от оснований пальцев).

В книге дается такой способ угадывания. Угадывающий просит кого-нибудь из компании сделать следующие действия, не называя получающихся чисел:

1) номер лица, имеющего кольцо, умножить на 2; спрашиваемый, в уме или на бумаге, выполняет:

2) к полученному произведению прибавить 5:

3) полученную сумму умножить на 5:

4) к произведению прибавить номер пальца, на котором находится кольцо:

5) сумму умножить на 10:

6) к произведению прибавить номер сустава, на котором находится кольцо:

Результат объявляется угадывающему.

От полученного числа последний отнимает 250 и получает: 702 - 250 = 452.

Первая цифра (идя слева направо) дает номер человека, вторая цифра - номер пальца, третья цифра - номер сустава. Кольцо находится у четвертого человека на пятом пальце на втором суставе.

Нетрудно найти объяснение этого приема, которого Магницкий не дает.

Пусть кольцо было у человека № а на пальце № b на суставе № с.

Выполним указанные действия над числами а, b, с:

1) а · 2 = 2а;

2) 2а + 5;

3) (2а + 5) · 5= 10а+ 25;

4) 10а+ 25 + b = 10а + 0 + 25;

5) (10а + b + 25) · 10 = 100а + 100 + 250;

6) 100a + 10b + 250 + с = 100a + 10b + с +250;

7) (100a +10b + с + 250) - 250 = 100a + 10b + с.

Получили число, в котором номер человека есть цифра сотен, номер пальца - цифра десятков, номер сустава - цифра единиц.

Третья забава. Считаем дни недели, начиная воскресенья: первый, второй, третий и так далее, до седьмого (субботы).

Кто-нибудь задумал день. Угадать, какой день он задумал.

Пусть задумана пятница - шестой день.

Угадывающий предлагает выполнить про себя следующие действия:

1) умножить номер задуманного дня на 2:

2) прибавить к произведению 5:

3) умножить сумму на 5:

4) приписать произведению в конце нуль и назвать результат:

От этого числа угадывающий отнимает 250 и получает

Был задуман шестой день недели - пятница. Обоснование правила такое же, как в предыдущем случае.

У Магницкого имеется и ряд более сложных математических забав.