Математика у русского народа

Письменные памятники математических знаний русского народа мы имеем начиная примерно с тысячного года нашего летосчисления. Эти знания являются результатом предшествовавшего долгого развития и основаны на практических нуждах человека.

Бирки - расчетные палочки

Рано возник в России интерес к науке в широких слоях населения. Сохранились сведения о школах при Владимире Святославовиче (978- 1015), при Ярославе Мудром (1036-1054). Находились в очень раннюю эпоху "числолюбцы", интересовавшиеся математикой не только в той мере, в какой она были нужна непосредственно для практической деятельности.

Примером таких "числолюбцев" был новгородский монах начала двенадцатого столетия Кирик.

Говоря об интересе русского народа к математике в те отделенные от нашего времени века, мы не должны забывать, что речь здесь идет о передовых слоях народа, стремившихся к знанию, строивших национальную культуру, которая пышно расцвела в последующие века.

Рядом с этими прогрессивными элементами имелись значительные круги духовенства и эксплуататоров, которые относились к знанию вообще и к математике в частности враждебно. Свидетельства о враждебном отношении к знанию мы встречаем еще в XVII и XVIII веках.

Основной предпосылкой для всех математических знаний служит нумерация, которая у разных древних народов имела различный вид.

По-видимому, все народы вначале обозначали числа зарубками на палочках, которые у русских назывались бирками. Такой способ записей долговых обязательств или налогов употреблялся малограмотным населением разных стран. На палочке делали нарезы, соответствующие сумме долга или налога.

Палочку раскалывали пополам; одну половину оставляли у должника или у плательщика, другую хранили у заимодавца или в казначействе.

При расплате обе половинки проверяли складыванием. В Англии этот способ записей налогов существовал до конца семнадцатого столетия. При ликвидации старых налоговых обязательств крестьян на дворе лондонского казначейства был устроен костер из накопившихся бирок. Этот костер оказался таким большим, что сгорело и само здание казначейства, а вместе с ним погиб и вделанный в стену образец английской меры длины, так что с тех пор англичане не знают точной длины своего фута.

Греки в шестом столетии до нашего летосчисления стали обозначать числа буквами, снабженными особым значком.

Таким же образом писали числа наши предки при помощи букв славянского алфавита, над которыми ставился особый значок - титло. Приведенная таблица показывает, какими буквами какое число обозначалось в славянской нумерации. Влиянием этой нумерации объясняются некоторые термины русского языка. В старых учебниках грамматики буква "и" называлась "и осьмиричное", буква "i" - "и десятиричное". Объясняются эти названия тем, что в славянской нумерации буква "и" обозначала 8, буква "i" - 10.

Славянская нумерация

Потребности хозяйственной жизни далекого прошлого довольствовались сравнительно небольшими числами - так называемым "малым счетом" наших предков. Он доходил до числа 10000, которое в самых старых памятниках называется "тьма", то есть темное число, которое нельзя ясно представить.

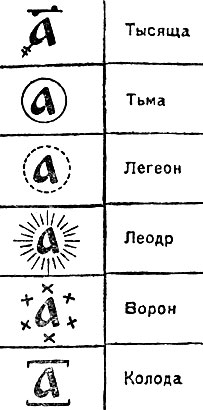
Славянская нумерация для обозначения больших чисел

В дальнейшем граница малого счета была отодвинута до 108, до числа "тьма тем". Старинная рукопись по этому случаю заявляет, что "больше сего числа несть человеческому уму разумети". Но наряду с этим "малым числом", "коли прилучался великий счет и перечень", употреблялась вторая система, называвшаяся "великим числом или счетом" или "числом великим словенским". В нем употреблялись более высокие разряды: тьма - 10⁶, легеон - 10¹², леодр - 10²⁴, ворон - 10⁴⁸; иногда еще колода - десять воронов - 10⁴⁹ (хотя нужно было за колоду принять, следуя системе, 10⁹⁶). Автор рукописи вновь заявляет, что "того числа несть больше".

Для обозначения этих больших чисел наши предки употребляли оригинальный способ, не встречающийся ни у одного из известных нам народов: число единиц любого из перечисленных высших разрядов обозначалось той же буквой, что и простые единицы, но обрамленной для каждого числа соответственным бордюром.

Греческие математики не додумались до этого способа письма даже в лице своих гениальных представителей.

Таких больших чисел не требовала в то время, и не требует и теперь, никакая практическая задача. Архимед, величайший греческий математик, сосчитал, что число песчинок во всем мировом пространстве, как это понимали в то время, не превышает 10⁶³.

Славянский "числолюбец" сказал бы, что это число песчинок не больше "тысячи легеонов воронов" (10⁶⁸ = 10³ · 10¹² · 10⁴⁸). Число песчинок во всем мировом пространстве человеку того времени действительно могло казаться наибольшим мыслимым числом, чем и оправдываются заявления авторов рукописей о том, что "больше сего не дано человеку разумети". Рассматривание большого славянского счета неоднократно в русских математических рукописях свидетельствует о том, что "числолюбцы" были достаточно многочисленны в древней Руси.

В первом печатном русском учебнике математики, в "Арифметике" Л. Ф. Магницкого^* (1703), даются уже интернациональные термины для больших чисел (миллион, биллион, триллион, квадриллион). Доходя до 1024 (квадриллиона), автор заявляет:

^*( В 1699 году в Амстердаме И. Ф. Копиевский напечатал "Руковедение в арытметику, сиречь во всякий счет", в котором на шестнадцати маленьких страницах изложены основы счисления. Книжка распространения в России не получила.)

 "Число есть бесконечно, 
 Умом нам не дотечно, 
 И никто не знает конца... 
 ........................
 ...............бездельно 
 Множайших чисел искати
 И больше сей писати
 Превосходной таблицы*. 
 ........................
 И еще кому треба 
 Счисляти, что внутрь неба, 
 Довлеет числа сего 
 К вещем всем мира всего".

^*(То есть доходящей до 1024.)

Славянская нумерация с принятием индусской потеряла всякое практическое значение.

Характерным "числолюбцем" древней Руси был упоминавшийся уже нами монах Кирик, и писавший в 1134 году книгу "Кирика - диакона Новгородского Антониева монастыря учение, им же ведати человеку числа всех лет".

Он подсчитывает с азартом, сколько месяцев, сколько дней, сколько часов он прожил, а затем считает в годах, в месяцах, в неделях и в днях время, прошедшее от сотворения мира до 1134 года (6644-го от "сотворения мира"), вычисляет день пасхи на будущее время. При исчислении времени Кирик употребляет "дробные часы", подразумевая под ними пятые, двадцать пятые, сто двадцать пятые (и так далее) доли двенадцатичасового дня. Доходя в этом счете до седьмого дробного часа, каковых во дне оказывается 937500, он заявляет: "больше сего не бывает", что, повидимому, означает, что более мелких делений дня не употребляли.

В "Русской правде", знаменитом правовом памятнике древней Руси, составление которого относят к промежутку времени между одиннадцатым и пятнадцатым столетиями, имеются статьи, посвященные вычислению потомства некоторого начального количества овец, коз и свиней. Вычислитель предполагает, что имеющееся число овец за год удваивается, и тогда, например, от двадцати двух озец через 12 лет будет стадо в 22 · 2¹² = 90112 овец, какой результат и дается в "Русской правде".

Это задача, которая примерно в то же время появляется в руководствах арифметики равных народов то о потомстве кроликов, то в виде задачи о вознаграждении изобретателя шахматной игры. Эти вычисления, повидимому, были созданием таких "числолюбцев", как упомянутый уже Кирик новгородский.

Естественно сопоставить со сказанным о математической культуре наших предков состояние математических знаний у народов, населяющих Западную Европу. Арифметические действия там производятся при помощи счетной доски (абака), на которую кладут камешки (бобы) или кружки с черточками^*. Наши счеты являются одним из вилов абака.

^*(Полагают, что поговорка "остался на бобах" ведет отсюда свое начало. Человек, проигравший все свои деньги, остался со своей счетной доской и с бобами, - "остался на бобах".)

Запись чисел производится при помощи громоздкой римской нумерации, в которой даже малые числа требуют большого количества знаков (например, 878 записывается так: DCCCLXXVIII), а запись больших чисел гораздо сложнее, чем в великом славянском счете. Наши современные цифры в Западной Европе появляются в книгах лишь в тринадцатом столетии, встречая сильное противодействие сторонников старого способа счета на абаке или при помощи римской нумерации.