
Геометрические сведения в старых русских памятниках
Развитие геометрии как науки подталкивалось практическими запросами жизни. Потребности земледелия, строительного и военного дела породили начала геометрии у всех народов, в том числе и у славян.
Уже в самых старинных памятниках русской истории мы встречаем начальные сведения по геометрии.
Земельной мерой наших предков служил участок, называвшийся "сохой". Это количество пахотной земли, которое был в состоянии обрабатывать один пахарь, - еще пример того, что и меры площади и их названия возникли из труда человека, из практики.
Размер сохи в разных местах был различный. От сохи образовывались меньшие меры - доли: 1/2 - полсохи, 1/4 - четь, 1/8 - полчеть, 1/16 - полполчеть, 1/32 - полполполчеть или малая четь и 1/3 - треть, 1/6 - полтреть, 1/12 - полполтреть, 1/24 - полполполтреть.
Исконно русским руководством, излагавшим приемы измерения площадей, является "Книга сошного письма", самый древний экземпляр которой относится к 1629 году, хотя имеются указания, что оригинал был составлен при Иване Грозном в 1556 году.
В этой книге при вычислении площадей фигур рекомендуется разбивать их на квадраты, прямоугольники, треугольники, трапеции. Площади квадрата и прямоугольника вычисляются по нашим правилам, площадь же треугольника находится как половина произведения основания на боковую сторону, и площадь трапеции - как произведение полусуммы оснований на боковую сторону (хобот). Последние правила, буквально понятые, неверны.
Возможно, что русская землемерная практика имела дело только с треугольниками и трапециями прямоугольными или почти прямоугольными, и в таком случае мы не имеем основания делать упрек нашим предкам в незнании правил начальной геометрии. В те отдаленные времена земля не являлась предметом купли-продажи, и точность результата измерения играла незначительную роль (см. раздел Математика у древних народов настоящего издательства).

Остроградский M.В. (1801-1861)
Оказывается, что в южнорусских губерниях, где свободной земли было много и она поэтому не ценилась, такие примитивные приемы оценки площадей применялись еще в XIX веке, что отразилось в биографических рассказах о знаменитом русском математике девятнадцатого столетия - М. В. Остроградском*. Он имел обыкновение шутить со своими слушателями и, между прочим, делить их на "землемеров" и "геометров".
*(Михаил Васильевич Остроградский (1801-1861), успешно занимавшийся математикой в только что открытом Харьковском университете, не мог получить там диплома за проявленное им недостаточное усердие по богословию. За него заступился ректор университета, также видный математик, Т. Ф. Осиповский, но дело кончилось увольнением из университета самого ректора. Остроградский вынужден был уехать в Париж и там стал слушать лекции математиков, которые вскоре заметили, что сидевший на последней скамейке длинноволосый студент моментально решал все предлагаемые с кафедры задачи. Остроградский стал любимцем всех парижских математических знаменитостей, которые устроили ему профессорскую кафедру в Париже, но его потянуло на родину, где он вскоре стал академиком и профессором.)
Когда его спросили о значении такого деления, он рассказал следующее:
"Еду я как-то по своей Полтавской губернии. Вижу - человек в поле с чем-то возится. Оказывается, землю мерит. Спрашиваю, - как он треугольный участок измеряет? Говорит, что перемножает длины двух сторон треугольника*. Спрашиваю: "Все ли у вас так делают?"
*(Деля, конечно, произведение на 2.)
Получаю ответ, что там, в губернии (губернские землемеры) как-то иначе поступают, а мы в уезде все так".
Не приходится удивляться, что такие приемы землемерия были в употреблении 500 лет назад в древней Руси.
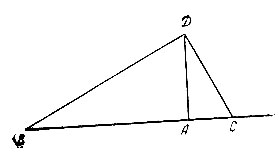
В 1607 и 1621 годах издается "Устав ратных, пушечных и других дел, касающихся до воинской науки". В этой книге между прочими сведениями даются и геометрические знания. Вот как определяется расстояние от точки наблюдения А до другой недоступной точки B.
В точке А нужно вбить шест AD примерно в рост человека. К верхнему концу шеста прилагается угольник так, чтобы вершина прямого угла совпала с концом шеста D, а продолжение одного из катетов проходило через точку В. Отмечается точка С на земле, через которую проходит продолжение другого катета. Если измерить расстояние АС, то искомое расстояние относится к длине шеста так, как последняя длина относится к расстоянию АС. При Иване Грозном, в 1556 году, было составлено первое русское руководство по землемерию под названием: "Книга, именуемая геометрия или землемерие радиксом и циркулем... глубокомудрая, дающая легкий способ измерять места самые недоступные, плоскости, дебри". А в середине XVI века была составлена первая общая карта Европейской России, которая, вместе с "чертежами Сибирских земель" 1667 года, считается самым замечательным памятником русской картографии. В одной из рукописей XVI века впервые упоминается "премудрый Клидас", то есть основоположник нашей современной геометрии - Евклид.
Пифагорова теорема является одним из самых важных положений всей геометрии. Она утверждает, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы или, другими словами, что сумма площадей квадратов, сторонами которые являются катеты прямоугольного треугольника, равна площади квадрата, стороною которого служит гипотенуза. Эту истину содержат ранние русские рукописи, хотя в них нет явного указания о том, что теорема имеет место только в прямоугольном треугольнике. Возможно, что ею пользовались для приближенного нахождения расстояния и в том случае, когда треугольник почти прямоугольный.

Заглавный лист первой книги по геометрии на русском языке
Во всяком случае, в рукописи начала XVII века мы встречаем такие, например, задачи:
"Хошь узнати промежь какими местами, не ходя и не меревь, что будет промежь верст, или сажен, или аршин. И ты познавай: как ходил будто к Троице в Сергиев монастырь и тут 32 версты. Ходил же в Воскресенский монастырь, и тут будто 24 версты. Что будет промежь теми монастырями скажи, не меревь?
И те числы с таких же чисел умножь. И те оба перечни сложи вместе и раздели на радикс [то есть извлекай квадратный корень]. И что из делу выдет, столько будет промежь теми местами верст".
Приводим чертеж и вычисления:
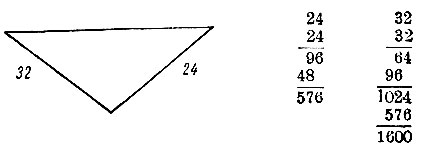
Ответ - 40.
Вторая задача такого же рода:
"Ходил с Москвы в Новгород и тут 600 верст. Ходил в Шуйский город и тут 500 верст. Что будет промежь теми городами: зри 781 верста".
Легко проверить, что 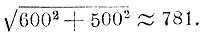 .
.
В 1625 году была переведена с английского языка книга по геометрии, доведенная до учения о круге. Эта рукопись представляет, повидимому, переделку "Начал" Евклида, то есть первую часть нашего обычного школьного учебника геометрии.
Книга Евклида впервые в печати на русском языке появилась в 1739 году под заглавием: "Евклидовы элементы в осьмь книг через профессора мафематики Андрея Фархварсона* сокращенные. С латинского на российский язык хирургусом Иваном Сатаровым преложенные. В Санкт-Петербурге, 1739". Продолжением этой книги являлись вышедшие в 1745 году "Архимедовы теоремы" в переводе того же Ивана Сатарова.
*(Андрей Фархварсон.- профессор Эбердинского университета - был приглашен Петром I в самом конце XVII века в Россию для преподавания в морских учебных заведениях.)
Через эти книги русскому читателю стало доступным всё существенное из классического наследия по элементарной геометрии.
Кроме того, еще в 1708 году вышел первый на русском языке печатный учебник геометрии под заглавием: "Геометриа словенски землемерие".
Менее чем через год было выпущено второе издание этой книги под заглавием: "Приемы циркуля и линейки или избраннейшее начало во математических искусствах, им же возможно легким и новым способом вскоре доступити землемерия и иных из оного происходящих искусств".

Букварь Кариона Истомина 1692 года. Изображены предметы, названия которых начинаются с буквы 'А'; среди них книга 'Арифметика' с индусскими цифрами, впервые появляющимися в русской книге
Новое издание книги вышло с оригинальными русскими иллюстрациями, так как рисунки первого издания, воспроизводившие сцены иностранной жизни, не отвечали требованиям русского читателя. Этот пример показывает, что в тех случаях, когда наши предки пользовались иностранными источниками, они их перерабатывали и приспосабливали к своей жизни. Самый же факт неоднократного переиздания книги свидетельствует о большом интересе к геометрии и к математике вообще в самом начале восемнадцатого столетия.
В это время у русских любителей математики уже имелась обширная оригинальная энциклопедия математики, посвященная в основном арифметике и алгебре, составленная Л. Ф. Магницким.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'