Зарождение математики

Математика у древних народов

В основе развития математики, как и всякой другой науки, лежат запросы практической деятельности человека.

"Возникновение и развитие наук обусловлено производством", - читаем мы у Ф. Энгельса. - "Как и все другие науки, математика возникла из практических нужд людей: из измерения площадей земельных участков и вместимости сосудов, из счисления времени и из механики"^*.

^*(Ф. Энгельс. Анти-Дюринг. Госполитиздат. 1948, стр. 87.)

Это положение подтверждает деятельность великого русского математика Пафнутия Львовича Чебышева.

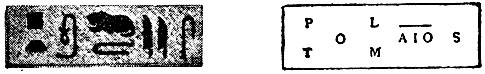
Иероглифическая надпись египтян и ее значение

Его самые оригинальные, совершенно новые для математики того времени, идеи возникли из изучения несовершенств ветряных мельниц, разных заводских установок, из решения чисто практических задач.

Совершенно ясно, что всякая наука вырастает из практики, ею питается и проверяется.

Отдельные математические знания, выросшие из практической деятельности человека, из наблюдения им явлений природы, суще* ствовали у различных народов древности.

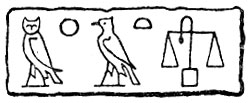
Слово 'весы', написанное египетскими иероглифами

В настоящее время мы хорошо знакомы с математическими знаниями обитателей древнего Вавилона (часть современного Ирака) и древнего Египта (берега реки Нила).

Наивысшего своего развития деятельность этих народов по созданию математики достигла около четырех тысяч лет назад.

В самые отдаленные времена практическая деятельность людей не могла обходиться без математических сведений. Сведения эти накапливались в течение тысячелетий, в эпохи, о которых не существует письменных памятников.

Но и в исторические эпохи жизни различных народов мы имеем большие периоды, которые не оставили имен мудрецов или ученых, и научные, в том числе и математические, достижения можно приписать только всему народу, его практической деятельности.

Прежде всего нужно рассказать о главнейших математических вопросах в древнем Египте.

Современная наука располагает сравнительно небольшим числом египетских математических документов. Их всего около пятидесяти.

Египетское иератическое, то есть упрощенное, письмо

Самым древним памятником египетской математики является так называемый "Московский папирус", относящийся к эпохе около 1850 года до начала нашего летосчисления.

Он был приобретен русским собирателем Голенищевым в 1893 году, а в 1912 году перешел в собственность Московскою музея изящных искусств.

Геометрическая задача Московского папируса. Изображена трапеция почти прямоугольная, что соответствует толкованиям русских математических рукописей

В этом папирусе среди других задач решается задача о вычислении объема усеченной пирамиды о квадратным основанием. Таких задач не содержится в других египетских памятниках. Этот памятник был изучен советскими учеными - академиками В. А. Тураевым и В. В. Струве.

По объему больше Московского папирус Ахмеса, найденный и приобретенный английским собирателем Райндом в 1858 году и потому часто называемый папирусом Райнда. Он относится к эпохе 1700 года до нашей эры. На русском языке он описан В. В. Бобыниным^*.

^*(В. В. Бобынин. Математика древних египтян. Москва, 1882. (Обновленная редакция в Журнале Министерства народного просвещения 1908 года.)

Папирус этот представляет собой полосу в 20 метров длиной и 80 сантиметров шириной.

В нем приведены образцы решения задач из области арифметики, геометрии и алгебры.

Все остальные математические документы Египта, последний из которых относится к тысячному году нашего летосчисления, повторяют те же правила вычислений, которые имеются уже в названных основных документах.

Оказывается, что египтяне четыре тысячи лет назад решали многие задачи нашей практической математики (арифметики, геометрии и на уравнения первой степени). Они имели нумерацию с десятичной основой, владели вычислениями при помощи дробных чисел.

Обрывок папируса Ахмеса

Задачи, которые мы решаем при помощи уравнений первой степени, они решали способом, который в нашей школе называется "способом предположений" (этот прием употреблялся до XVIII века в арифметике всех народов под названием "способа ложного положения" или "фальшивого правила").

Решали египтяне и задачи на прогрессии. Они умели вычислять площади прямолинейных фигур и круга; отношение длины окружности к ее диаметру - наше число π - согласно правилам египетской геометрии оказывается равным 3,10; по мнению некоторых исследователей, египтяне знали правило для вычисления объема шара и, несомненно, умели вычислять объем усеченной пирамиды с квадратным основанием.

Одновременно с зарождением математики в Египте жители древнего Вавилона - шумеры - самостоятельно создали свою математику. Шумеры писали знаками, составленными из клиновидных черточек, на глиняных плитках, которые после сушки на палящем солнце приобретали большую прочность. В настоящее время эти глиняные плитки тысячами находят при раскопках.

В Ленинграде в Эрмитаже и в Московском музее изящных искусств имеется большое количество египетских и вавилонских памятников с подлинными надписями. Египетские надписи сохранились и на сфинксах, стоящих в Ленинграде на берегу Невы перед зданием Академии художеств.

За последние двадцать-тридцать лет найдено и изучено громадное количество вавилонских математических памятников.

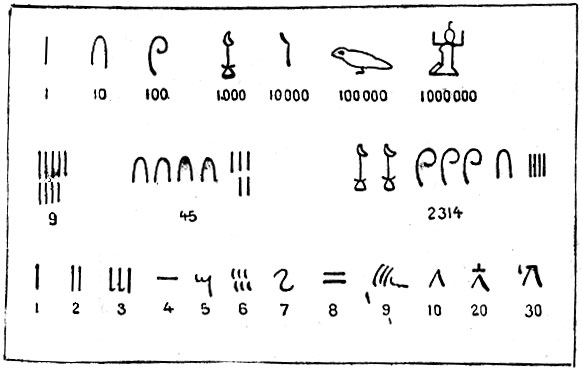
Египетские цифры: верхние две строки написаны иероглифами; нижняя строчка написана иератическими знаками

Ученые нашли математическую энциклопедию вавилонян на сорока четырех таблицах, представляющую как бы сводку всех математических достижений шумеров к эпохе около двухтысячного года до нашего летосчисления, то есть к моменту наивысшего расцвета вавилонской культуры. Из этой энциклопедии видно, что вавилоняне в то отдаленное время лучше применяли на практике математические знания, чем греки на 1600 лет позднее, хотя до сих пор некоторые ученые считают греков основоположниками математической науки.

Задача на уравнение, записанная иероглифическим письмом. Читается справа налево: 'Куча (неизвестное), 2/3, 1/2, 1/7, целое составляет 33', то есть x+2/3x+1/2x+1/7x = 33

Вавилоняне были основоположниками науки астрономии. Их наблюдения послужили основой греческой астрономии; от них до нас идет семидневная неделя, деление круга на 860 градусов, деление часа на 60 минут, минуты на 60 секунд, секунды на 60 терций. У вавилонян же зародилась астрология - мнимая наука об определении будущего по звездам.

Вавилоняне создали совершенное для своего времени исчисление, в основе которого лежало не число 10, как у нас, а число 60, что во многих случаях облегчало труднейшее арифметическое действие - деление.

Они же создали систему мер и весов, которая предвосхитила все преимущества нашей метрической системы (каждая мера была в 60 раз больше предыдущей, откуда и ведет начало наше деление углов и мер времени).

Клинообразные письмена вавилонян

Вавилоняне решали уравнения второй степени и некоторые виды уравнений третьей степени (европейцы научились решать такие уравнения только в XVI веке).

Вавилонская глиняная плитка

Со второй половины второго тысячелетия до начала нашего летосчисления на территории, лежащей между царствами Вавилонским и заменившим его Ассирийским, с одной стороны, и Закавказьем, с другой стороны, существовало Ванское царство или царство Урарту, которое в VIII веке захватывает области южного Закавказья.

Народы Урарту, усвоив вавилонскую математику, переработали ее. Установлено, что они перешли к десятичной нумерации, близкой к нынешней позиционной десятичной и резко отличной от египетской десятичной нумерации, которая не знала позиционного принципа.

Урартская арифметика во многом сходна с древне-армянской.

Таким образом, математика древних вавилонян через народы Урарту оказала влияние на древнейшую математическую культуру закавказских народов, в особенности армянскую, содействовав исключительно раннему ее расцвету.

Параллельно с Египтом и Вавилоном шло развитие математики в Индии.

За две или полторы тысячи лет до начала нашего летосчисления были написаны древние индусские книги, называемые ведами.

В этих книгах и их переделках, в так называемых сутрах, содержатся подробные правила для замены одной фигуры равновеликой ей другой, для разделения и складывания этих фигур.

Правила вед выполнялись главным образом при помощи прямоугольных треугольников, стороны которых выражаются целыми числами. Ведам известны целочисленные прямоугольные треугольники следующих видов:

1) со сторонами 8, 4, б и ему подобные, получаемые от умножения чисел 3, 4, 5 на одно и то же число;

2) со сторонами 5, 12, 13 и ему подобные;

3) со сторонами 8, 15, 17 И 12, 35, 37. Прямоугольные треугольники обладают тем свойством, что сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора). Этому требованию удовлетворяют треугольники о указанными выше вычисленными сторонами. Например:

Построение фигуры иной формы, которая была бы точно равновелика данной, и родственные задачи составляют существенную часть и греческой геометрии и изучаются в нашем школьном курсе.

Задача складывания фигур квадратной, треугольной или многоугольной формы из квадратных плит или кирпичей, которую ставило строительное искусство, по всей вероятности, дало начало учению о треугольных, квадратных и вообще многоугольных числах.

Треугольными назывались числа: 1, 3, 6, 10, 15 и так далее; квадратными - 1, 4, 9, 16, 25 и так далее. Если изобразить кирпичи точками, то эти числа представляют количество кирпичей, необходимых для построения треугольной или квадратной фигуры при постепенном увеличении сторон их, как показывают чертежи:

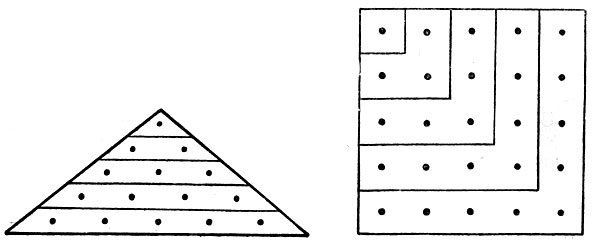
Квадратные плиты (кирпичи) были основным строительным материалом в Индии и в особенности в соседнем с ней Вавилоне, совершенно лишенном камня и дерева. Равновеликость фигур определялась по числу этих плит.

Эта практическая задача строительного искусства выдвинула вопрос об определении целого числа плит, необходимых для получения треугольной, квадратной или многоугольной фигуры о заданной величиной площади.

Подпись царя Ксеркса клинописью

Решение этой задачи требовало изучения свойств последовательностей чисел натурального ряда: 1, 2, 3, 4, . . . треугольных: 1, 3, 6, 10, 15, . . . квадратных: 1, 4, 9, 16, . . . Этими вопросами занимались вавилоняне, индусы, а позднее - греческие математики, начиная с Пифагора.

В жизнеописаниях Пифагора (VI век до начала нашего летосчисления) рассказывается о пребывании его в Египте, Вавилоне и Индии. С другой стороны, Пифагору приписывается такое количество открытий в области геометрии и учения о числах, которые никак не могли быть сделаны в течение одной жизни.

Естественно возникает мысль о том, что многие открытия, приписываемые Пифагору, были им вынесены из Вавилона, Индии и Египта, в частности учение о многоугольных или фигурных числах (треугольных, четырехугольных: и так далее), связанных с вопросами строительного искусства этих стран.

Самым ценным вкладом индусов в сокровищницу математических знаний человечества является употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 8, 4, 5, 6, 7, 8, 9, 0.

Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место определяется нулями, приписываемыми к цифре.

Окончательная разработка такой поместной, или позиционной, системы нумерации, идея которой была у вавилонян, есть величайшая заслуга индусов.

Французский математик Лаплас (1749-1827) пишет по этому поводу: "Мысль - выражать все числа немногими знаками, придавая им кроме значения по форме еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна. Как нелегко прийти к этому, мы видим ясно на примере величайших гениев греческой учености - Архимеда и Аполлония, от которых эта мысль осталась скрытой".

Вавилонское письмо

Великое открытие поместной системы нумерации было сделано не каким-нибудь гениальным человеком. Это открытие, как и все открытия египтян и вавилонян, являются результатом долгого постепенного обогащения опыта и наблюдения целого народа. Таковы же многие, на первый взгляд весьма абстрактные, задачи математики.

У греков возникли четыре замечательные задачи, которыми человечество занималось свыше двух с половиною тысячелетий. Задачи эти следующие:

1. Разделить окружность или дугу на произвольное число равных частей (построить в окружности правильный многоугольник о любым числом сторон).

2. Удвоить куб, то есть построить куб, который имел бы объем в два раза больший, чем данный куб.

3. Разделить любой угол на три равные части.

4. Построить квадрат, имеющий площадь, равную площади данного круга.

Все эти задачи требовалось решать точно, пользуясь только циркулем и линейкой, на которой нет делений.

Несмотря на свою кажущуюся простоту, они оказались не разрешимыми циркулем и линейкой, что было установлено лишь ко второй половине XIX века.

До этого времени, а отчасти и после него, очень многие люди, в особенности из числа любителей математики, не изучившие серьезно этой науки, тратили время и силы на безнадежные попытки решения этих задач.

История этих задач, о которых написано много книг и брошюр и на русским языке, потребовала бы отдельной книги, из которой можно было бы узнать, как из бесплодных попыток решись эти, на первый взгляд очень простые, задачи выросли очень важные отрасли современной математической науки.