1. Понятие нормального решения

(Комментарий. В предыдущей главе мы рассматривали несовместные системы, ввели понятия псевдорешения, как решения, минимизирующего невязку, нормальной СЛАУ; нормального псевдорешения, как решения, полученного нормализацией СЛАУ. Здесь мы разберём недоопределённые, то есть совместные неопределённые СЛАУ.

Альтернатива Фредгольма, с помощью которой проводится анализ СЛАУ, имеет вид:

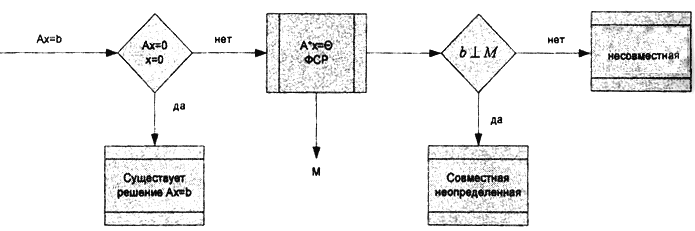
У совместных недоопределённых СЛАУ невязка равна нулю, а решений бесконечно много. Выбор единственного решения из них обычно осуществляется исходя из требования минимизации нормы полученных решений.)

Определение. Решение, удовлетворяющее требованию минимальности нормы, называется нормальным решением.

Пример. Рассмотрим СЛАУ:

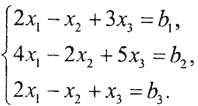
1. При каких b_i система будет совместна? Найти нормальное решение в этом случае.

2. При каких b_i система будет несовместна? Найти нормальное решение в этом случае.

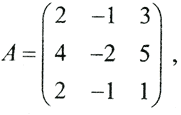
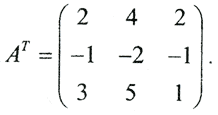
Решая систему A^Tx=Θ, получаем фундаментальную совокупность решений (ФСР): (3,-2,1). Возьмем, например, вектор b^_=(2,3,0). В этом случае СЛАУ совместна, но недоопределена. Невязка равна нулю. Рассмотрим уравнение Ax^_=b^_, то есть

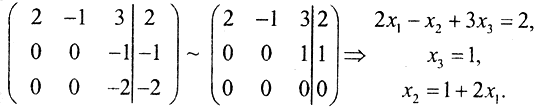
Получим нормальное решение:

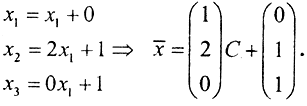
Это решение надо минимизировать: ||x||²=x₁²+x₂²+x₃² ⇒ x²=C²+(2C+1)²+1=5C²+4C+2, 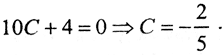Тогда точка минимума 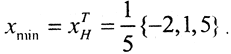отсюда 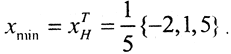Найдём нормальное псевдорешение этой системы. Для этого воспользуемся следующим равенством: A^TAx=A^Tb, A^*=A^T. Так как 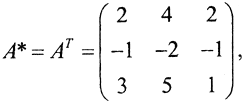то

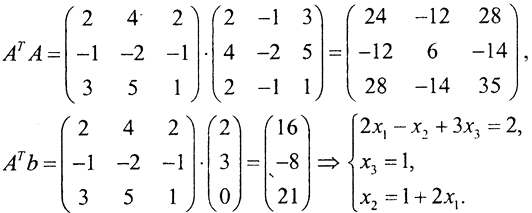
Теперь x₁=C, x₂=2C+1, x₃=0C+1. То есть 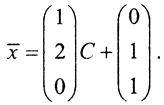Таким образом, решение нормальной системы, то есть нормальное псевдорешение совпадает с нормальным решением исходной системы. Нормальное решение - это наиболее гладкое из решений.

Выбор единственного решения из множества решений вырожденной СЛАУ может быть осуществлен методом псевдообратной матрицы Мура Пенроуза. Сначала Мур (1920), а потом Пенроуз (1955) предложили использовать в роли аналога обратной матрицы для произвольной прямоугольной матрицы A псевдообратную матрицу A⁺.