7. Априорная информация о решении

Понятие неклассического решения связано с изменением представления о самой модели. Теперь она должна включать в себя и априорную информацию о возможном характере предполагаемого решения, по крайней мере уменьшающую информационную неопределённость, и алгоритм обработки информации, то есть получения "решения".

(Комментарий. Эта ситуация напоминает квантовую механику. В основу квантовой механики положены два понятия: понятие состояний и понятие наблюдаемых. Состояния это векторы в гильбертовом пространстве; наблюдаемые (то есть динамические переменные микрообъектов такие, как координата, энергия, импульс и т. д.) эрмитовы операторы, действующие на векторы состояния. Возможные значения наблюдаемых сопоставляются с собственными значениями этих операторов, то есть акту наблюдения сопоставляется определённая процедура получения решения операторного (дифференциального) уравнения (практически, всегда численными методами), а возможными значениями наблюдаемых объявляются результаты этих вычислений. То есть модель квантово-механического объекта - это сложная конструкция, включающая в себя и алгоритм её получения, и априорную информацию об объекте, и способы интерпретации. С другой стороны, здесь просматривается аналогия с понятием "конечной точности" по Колмогорову, когда вместо "невычислимого" решения рассматриваются либо сглаженные в определённом смысле решения, либо функционалы от них. В любом случае параметры алгоритма сглаживания и сам алгоритм становятся частью исследуемой системы.)

Введение априорной дополнительной информации об искомом решении является необходимым элементом решения некорректных задач. Существуют два основных подхода к заданию априорной информации - детерминистский и вероятностный.

B первом случае априорная информация заключается в указании класса допустимых решений, то есть подмножества в пространстве решений, в котором оно ищется. Такая априорная информация называется детерминистической или информацией типа D. Она может носить количественный характер, что позволяет сузить класс возможных решений, например, до компактного множества и сделать задачу физически определённой. Она бывает двух типов: или указывается подпространство, в котором ищется решение (D1), или допустимыми решениями считаются только те векторы, норма которых не превосходит заданной величины, то есть все они принадлежат некоторому гипершару радиусом R (D2). Таким образом, детерминистическая априорная информация нетривиальна и рассматривается в явном и неизменном виде, что позволяет придать ей явный физический смысл.

В этом случае в основе понятия приближённого решения некорректной по условию задачи Ax=y лежит идея А. Н. Тихонова [21], что решение некорректной задачи можно представить как приближенное вычисление значений разрывной функции. В общем случае пределом последовательности непрерывных функций является разрывная функция. Тогда можно построить алгоритм, позволяющий получить приближённое решение обратной некорректной задачи Ax=y с любой заданной точностью, каждый раз решая прямую корректную задачу x_α=R_αy. Пусть, для определённости, в уравнении Ax=y пространства X=C[a,b] и Y=L₂[c,d] или любые нормированные пространства. Непрерывный линейный оператор R_α называется регуляризирующим, если ∃α ∈(0,α₀) - не очень большое, в пределах которого оператор R_α имеет область определения Y и для любой функции x_α∈X, такой, что Ax_α=y_α - приближённое решение x_ε=x_δ(ε), такое, что ∀ ε > 0 ∃ δ = δ(ε): (||y_α-y_δ||<δ⇒ ||x_α-x_ε||<ε).

То есть при применении оператора R_α к y приближённое решение уравнения Ax=y существует и 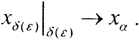Это решение при стремится к точному и при каждом задача корректна по Адамару. С другой стороны, ∃α=α₀, при котором регуляризация будет наилучшей. Если α очень велико или очень мало, то это не регуляризация. При α=0 оператор R_α должен совпасть с обратным, а он неограничен. Таким образом, приближённое решение некорректной задачи может быть сведено к нахождению регуляризирующего оператора R_α, который определяет устойчивое приближение к решению x. Решение x_α и называют устойчивым точным решением некорректной задачи.

(Комментарий. Можно ли любую разрывную функцию представить как предел последовательности непрерывных функций? В начале XX века Р. Бэр дал классификацию разрывных функций, в которой функции, являющиеся пределом последовательности непрерывных функций, он назвал аналитически представимыми функциями первого класса. В. Винокуров показал, что в банаховых пространствах множество регуляризируемых функций совпадает со множеством аналитически представимых функций первого класса ( ДАН СССР, 1975, т. 220, № 2). Применив к ним процедуру предельного перехода получим аналитически представимые функции второго класса и т. д. Функции, относящиеся к классам выше первого, не могут быть регуляризированы в принципе.)

Таким образом, что бы мы ни понимали под "решением" некорректной задачи, существует широкий класс принципиально неразрешимых, то есть нерегуляризируемых задач, для которых справедлив "принцип неопределённости": при увеличении точности входной информации ошибка решения только растёт и не может быть меньше некоторой константы. Теперь все возможные задачи можно разбить на три класса:

• корректные задачи, для которых метод регуляризации не нужен;
• некорректные задачи, для которых существует регуляризирующий их алгоритм;
• нерегуляризируемые некорректные задачи.

Другой подход основан на введении распределения вероятностей в пространстве решений. B этом случае априорная информация о решении вносится путём задания некоторой плотности распределения вероятностей P(x). Такое задание априорной информации называется стохастическим или информaцией типа S. Различные варианты метода стохастической регуляризации соответствуют различным способам задания априорного распределения вероятностей. Любая обратная некорректная задача в приложениях это задача обрботки экспериментальных данных, ошибки которых естественно трактовать вероятностным образом. Метод работает как обучаемая система. Результат эксперимента y_δ интерпретируется как условная плотность вероятности измерения P(y_δ|x) при условии, что плотность вероятности решения P(x) известна. Требуется найти апостериорную плотность вероятности решения P(x|y_δ) при условии, что получен результат эксперимента y_δ. Получив после серии экспериментов апостериорную плотность вероятности решения P(x|y_δ), её можно в следующей серии рассматривать как априорную плотность распределения вероятностей решения P(x).

Рассмотрим алгебраизированное операторное уравнение I рода Ax=y_δ, то есть уравнение, в котором и x и y_δ принадлежат конечномерным эвклидовым пространствам Rⁿ и R^m. При этом не имеет значения, существует или нет точное решение этого уравнения, а число уравнений может в любую сторону отличаться от числа неизвестных. Тогда по формуле Байеса 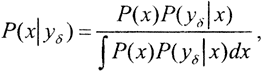где знаменатель - это условие нормировки. Метод был предложен и подробно изложен В. Ф. Турчиным (УФН, 1970, т. 102, вып. 3). В силу ограниченности объёма этой книжки мы не будем на нём останавливаться.

В соответствии с тремя перечисленными типами априорных ограничений можно выделить три основные группы методов решения обратных некорректных задач:

Но в любом случае модель задачи содержит в себе и априорную информацию о решении, и метод решения задачи, включая алгоритм обработки информации, то есть получения "решения".