2. Что такое модель

При изучении реального объекта или явления первый этап - построение теоретической модели (франц. мodelle - образец) этой реальности. При построении теоретической модели некоторые факты, известные лишь с некоторой (даже очень большой) долей вероятности или лишь с некоторой (даже очень большой) точностью, признаются "абсолютно" верными и принимаются за "аксиомы". Смысл этой "абсолютности" состоит в том, что мы работаем с моделью так, как если бы она совпадала с реальностью. Далее, по определённым правилам интерпретации эти "аксиомы" формулируются на языке математики и дальнейшая работа с ними происходит по правилам формальной логики и математики, то есть "теоремами" объявляется все то, что из них можно вывести.

(Комментарий. Математику и/или логику можно представить как ядро любой проблемы, имеющей отношение к любой интеллектуальной деятельности человека. Это ядро окружают модели реальности, создаваемые в конкретных предметных областях, вне которых и находится внешний мир. Однако, являясь естественным общезначимым средством науки, математика не может решать никаких проблем ни в одной из предметных областей. То есть никакая математика не может подтвердить никакую теорию. Она может только обнажить проблему, выявить её внутренние противоречия.)

Подчеркнём, что модель должна принадлежать математической теории (не обязательно формальной), то есть не должна апеллировать к каким-либо реальным понятиям или аргументам извне. "Математики имеют дело только со структурой рассуждений, и им, в сущности, безразлично, о чем они говорят. В физике вы должны понимать связь слов с реальным миром"[24]. Математическая теория, дополненная набором правил интерпретации, связывающих теоретические величины с нашими наблюдениями, и есть теоретическая или физическая модель реальности. Поскольку она построена по законам математики, то конечное число исходных аксиом 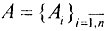представляет собой достаточные условия для получения любого следствия из них. Таким образом, теоретическая модель реальности есть совокупность аксиом, правил вывода и полученных с их помощью теорем, дополненная правилами интерпретации, работающими только на "входе" и "выходе". Эта совокупность исходных аксиом и правил интерпретации, то есть "перевод" математической задачи на предметный язык и наоборот, и есть простейший источник некорректности.

Пример. Решением уравнения x + y = 5 является пара {x,y}={t,5-t}, t ∈ R. Однако задача "У Маши и Миши пять игрушек. Сколько игрушек у каждого из детей?" уже некорректна, потому что её нельзя решить однозначно.

(Комментарий. 1. Уравнения подобного рода могут быть источником некорректности "физической" задачи. В теории уравнений (дифференциальных и интегральных) уравнения, которые заведомо могут быть источником некорректности "физической" задачи тоже часто называют некорректными. В дальнейшем мы также будем пользоваться этой терминологией.

2. Ясно, что в импликации A ⇒ B если B истинно, то A может быть как истинным, так и ложным. Кроме того, B истинно и при других возможных A, даже не пересекающихся с данным A. Правила интерпретации должны позволять зкспериментальную проверку B. Но, как уже отмечалось, никакой эксперимент не может подтвердить никакую теорию, то есть адекватность реальности исходных положений A.)